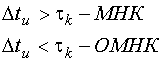Обобщенный метод наименьших квадратов (ОМНК)

ОМНК при малом объеме выборки

ОМНК при большом объеме выборки

Метод максимального правдоподобия

Метод наименьших квадратов

Этот метод применяется в основном в случае линейной параметризации.

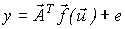
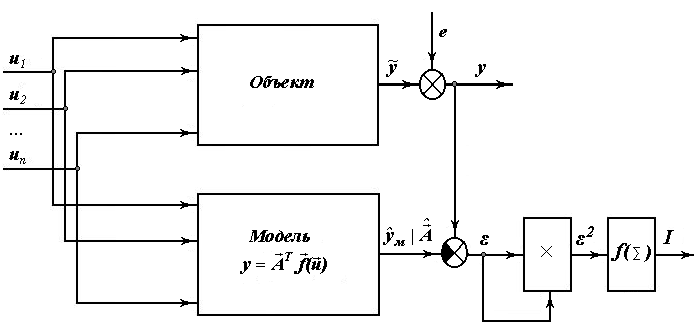
Найдем оценку вектора .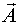

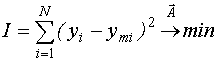- запись экстремальной задачи.

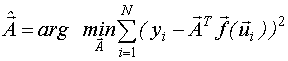- запись аргументной задачи.

,

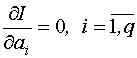
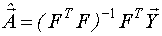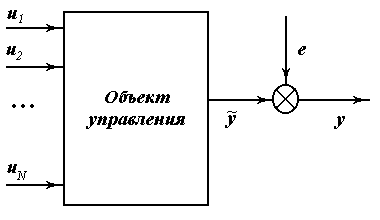
где 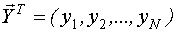- вектор значений выхода объекта управления в N измерениях;

F - матрица базисных функций размерностью N*q.

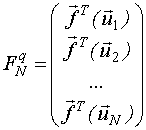
Пример.

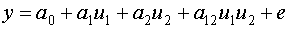
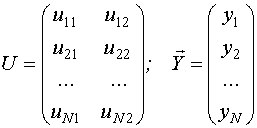
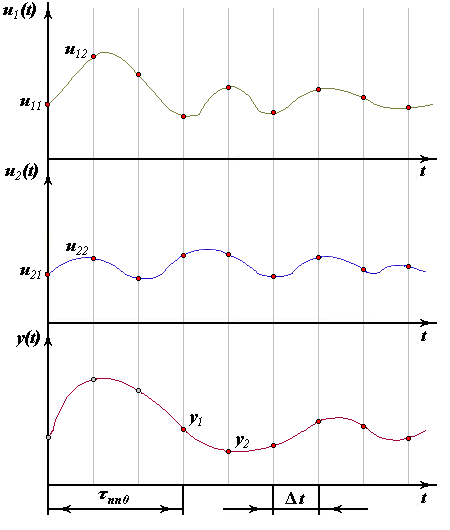
где 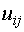- значение i-го входа при j-ом измерении;
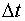- шаг дискретизации.

Выходной сигнал снимается через время переходного процесса после изменения значений входов.
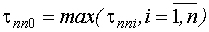- время переходного процесса.

Для определения времени переходного процесса необходимо определить время переходного процесса каждого канала, для чего подать поочередно на каждый вход ступенчатое воздействие при стабильных остальных входах.

Время наблюдения выхода больше времени наблюдения входа.

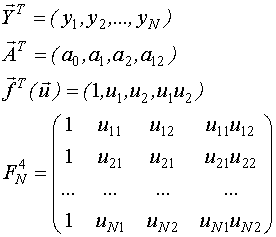
Ковариационная матрица оценок вектора 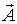равна: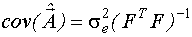

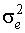- дисперсия внешнего шума.

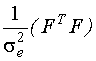- информационная матрица Фишера.

Характерно, что информационная матрица Фишера и ковариационная матрица оценок зависят только от входа объекта управления и не зависят от выхода, то есть они однозначно определяются значениями входных переменных и не зависят от значений выходных переменных.

Ковариационную матрицу точно вычислить невозможно, так как неизвестна дисперсия внешнего шума, но если оценить дисперсию внешнего шума, то можно найти оценку ковариационной матрицы.

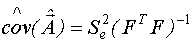
Уравнение, полученное в результате применения метода наименьших квадратов, называется уравнением регрессии.

Регрессия - это условное математическое ожидание или зависимость математического ожидания выходного параметра объекта от входных детерминированных переменных.

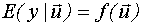
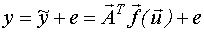
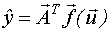- уравнение регрессии

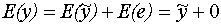
Так как E(e)=0 (e - центрированная случайная величина)

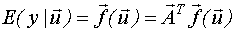
Структура уравнения регрессии совпадает с описанием объекта, когда случайная величина e(t) имеет нулевое математическое ожидание. В результате эксперимента можно найти лишь оценку уравнения регрессии 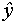- предсказанное по уравнению регрессии значение выхода, которое является случайной величиной и зависит от вектора входных параметров .
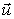Математическое ожидание :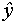

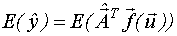
Пример.


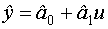
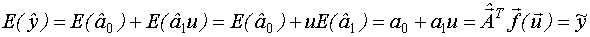
- если оценки неизвестных коэффициентов несмещены.

Дисперсия предсказания значений выхода имеет следующий вид: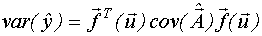
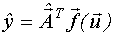- дисперсионная функция модели регрессии.
Дисперсионная функция позволяет оценить точность предсказания выхода по модели при различных значениях входных переменных.

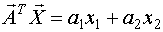- линейная форма

при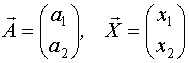

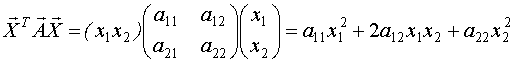- квадратичная формa.
Корреляционная функция случайного процесса и ее свойства

Пусть x(t) - случайный процесс.
Автокорреляционной функцией случайного процесса x(t) называется функция

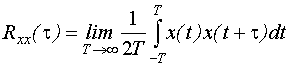
Случайный процесс-это функция, значения которой в каждый фиксированный момент времени являются случайными величинами.
Случайные процессы могут быть эргодическими и неэргодическими.

Процесс называется эргодическим, если его моментные характеристики, полученные по одной реализации, совпадают с теми же характеристиками, полученными по ансамблю реализаций. Таким образом, если процесс эргодический, то оценки математического ожидания и дисперсии этого процесса, полученные по одной бесконечно длинной реализации и по любому сечению бесконечно большого ансамбля реализаций, будут совпадать. Свойство эргодичности может иметь место только для стационарных случайных процессов.

Процесс называется стационарным, если его математическое ожидание и дисперсия не зависят от времени.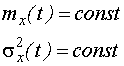

Если математическое ожидание и дисперсия случайного процесса зависят от времени, то процесс называется нестационарным.

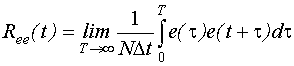
Для вычисления корреляционной функции случайного процесса необходимо иметь бесконечно длинную реализацию этого процесса. На практике может быть найдена лишь оценка автокорреляционной функции, так как реализация ограничена.

Для получения реализации случайного процесса необходимо провести следующий эксперимент: при стабильном входе зафиксировать значение выхода, далее необходимо определить математическое ожидание выходной переменной.
Реализация случайного процесса получается вычитанием из реализации выходного процесса математического ожидания выходного процесса.
На практике вычисляются ординаты оценки автокорреляционной функции по следующей формуле:

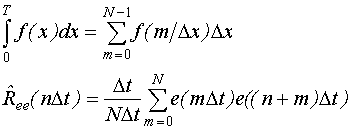
Данная формула пригодна в том случае, если автокорреляционная функция случайного процесса e(t) определяется не на основе всех имеющихся отсчетов процесса e(t), а на основе части этих отсчетов. В качестве "хвоста" можно использовать столько точек, сколько координат автокорреляционной функции мы хотим вычислить. Обычно число вычисляемых ординат должно быть в 2-3 раза больше дискретного времени памяти объекта: .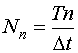

В этом случае в обработке участвуют все ординаты участка e(t). Недостатком этой формулы является то, что оценки ординат автокорреляционной функции вычисляется по выборкам различных объемов. Соответственно точность уменьшается с увеличением номера ординаты.

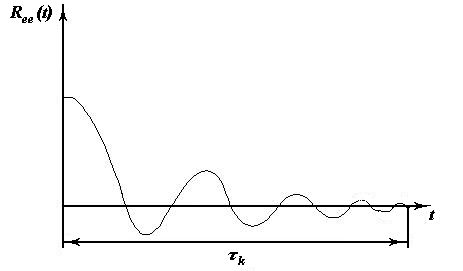
Получив оценку автокорреляционной функции, можно найти время корреляции случайного процесса e(t) - .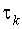

Время корреляции 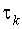- это время затухания автокорреляционной функции до достаточно малой величины.

Наша функция не должна выходить за пределы ограничений и тогда определяется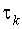

Метод наименьших квадратов применим, если измерение времени выхода происходит с интервалом не меньше времени корреляции ( ).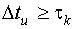

Таким образом, последовательность выбора метода оценивания в случае непрерывной реализации входа-выхода должна быть следующей:

1. находится время корреляции;

2. задается структура модели и определяется число неизвестных коэффициентов(q);

3. определяется минимально необходимое число измерений (N) из условия ;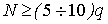

4. определяется 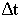- интервал съема данных из условия ;

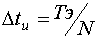5. правило выбора: если