ГБОУ ВПО КрасГМУ им. проф. В.Ф. Войно-Ясенецкого Минздравсоцразвития России

Утверждаю

Проректор по учебной работе

ГБОУ ВПО КрасГМУ Росздрава

проф. Никулина С.Ю. _________

« » 2012 г.

Контрольно - измерительные материалы

к экзамену по дисциплине «Дифференциальное и интегральное исчисление»

для студентов специальности 060609 – Медицинская кибернетика (очная форма обучения)

Тестовые задания

ОСНОВЫ теории ДИФФЕРЕНЦАЛЬНых уравнений

Выберите правильный ответ

1. Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы называется

1) аналитическим

2) алгебраическим

3) дифференциальным

2. Порядок дифференциального уравнения определяется порядком входящей в него

1) функции

2) аргумента

3) высшей производной

4) низшей производной

3. Общим решением дифференциального уравнения является функция

1) y=F'(x)

2) y=F(x)+C

3) y=F' (x)+C

4) y=x+C

4. Уравнение вида называется дифференциальным уравнением

1) с разделяющимися переменными

2) с разделенными переменными

3) линейным

4) однородным

5. Уравнение вида называется дифференциальным уравнением

1) с разделяющимися переменными

2) с разделенными переменными

3) линейным

4) однородным

6. Решением дифференциального уравнения является функция, при подстановке которой в исходное уравнение

1) оно обращается в тождество

2) правая часть равняется нулю

3) оно не изменяется

4) левая часть равняется нулю

7. Общее решение дифференциального уравнения представляет

1) одну функцию

2) множество функций, отличающихся на постоянное число

3) производную функции

4) дифференциал функции

8. Частное решение дифференциального уравнения представляет

1) одну функцию

2) множество функций, отличающихся на постоянное число

3) производную функции

4) дифференциал функции

9. Общим решением дифференциального уравнения является функция

1)

2)

3)

4)

10. Общим решением дифференциального уравнения является функция

1)

2)

3)

4)

11. Общим решением дифференциального уравнения является функция

1)

2)

3)

4)

12. Дифференциальное уравнение первого порядка называется однородным, если его можно представить в виде

1) y′=f(x+y, C)

2) y′=f(x–y, C)

3) y′=f(x×y, C)

4) y′=f(y/x, C)

13. Решением дифференциального уравнения y′=1+y/x, является функция

1) y=Сe^-y/x

2) y=Сe^x

3) y=Сe^y×x

4) y=Сxe^y

14. Решением дифференциального уравнения y²+x²y′=0, является функция

1) y=Сe^y/x

2) x+y=Cxy

3) y=e^Cy×x

4) x–y=Cxy

15. Решением дифференциального уравнения y′–y/x=y²/x², является функция

1) y=xln|Cx|

2) y=-ln|Cx|+x

3)

4)

16. Решением дифференциального уравнения y′–y/x=x²/y², является функция

1) y=x³+ln|Cx|

2)

3)

4)

17. Решением дифференциального уравнения y′–y/x=x²+1, является функция

1)

2) y=x³lnx+Cx

3) y=x³+ln|Cx|

4) y=x³+lnx+Cx

18. Если общее решение дифференциального уравнения y=xe^Cx+1, то для y(1)=1 частное решение равно

1) y=e^С+1

2) y=e^x+1

3) y=xe^x+1

4) y=xe^-x+1

19. Если общее решение дифференциального уравнения x+y=Cxy, то для y(1)=1 частное решение равно

1) Cxy=2

2) x+y=xy

3) x+y=2xy

4) x–y=xy

20. Уравнение xy′′= y′, является дифференциальным уравнением второго порядка, не содержащем в явном виде

1) независимую переменную

2) неизвестную функцию

3) аргумент функции

4) первую производную функции

21. Уравнение (y′)²=yy′′, является дифференциальным уравнением второго порядка, не содержащем в явном виде

1) независимую переменную

2) неизвестную функцию

3) аргумент функции

4) первую производную функции

22. Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение

1) y′=f(x)

2) y′′= f(y)

3) k²+pk+q=0

4) y′′+py′+qy=0

23. Характеристическим уравнением называется уравнение вида

1) y′=f(x)

2) y′′= f(y)

3) k²+pk+q=0

4) y′′+py′+qy=0

24. Порядок дифференциального уравнения второго порядка, не содержащего в явном виде искомую функцию можно понизить с помощью замены

1) y′=u(x), y′′= u′(x)

2) y′=p(y),

3) y′=u(x),

4) y′=p(y), y′′= u′(x)

25. Порядок дифференциального уравнения второго порядка, не содержащего в явном виде независимую переменную можно понизить с помощью замены

1) y′=u(x), y′′= u′(x)

2) y′=p(y),

3) y′=u(x),

4) y′=p(y), y′′= u′(x)

26. Дискриминант характеристического уравнения, имеющего действительные и различные корни

1) D<0

2) D=0

3) D>0

27. Дискриминант характеристического уравнения, имеющего действительные и равные корни

1) D<0

2) D=0

3) D>0

28. Дискриминант характеристического уравнения, имеющего комплексные и сопряженные корни

1) D<0

2) D=0

3) D>0

29. Для уравнения y′′+y=0, характеристическое уравнение будет иметь вид

1) k²+1=0

2) k²+k=0

3) k²+k+1=0

4) 2k+1=0

30. Для уравнения y′′+6y′+y=0, характеристическое уравнение будет иметь вид

1) k³+6k²+1=0

2) k²+6k+1=0

3) 6k²+k+1=0

4) 6k+1=0

31. Корни характеристического уравнения k²+1=0, равны

1) k_1,2=1

2) k_1,2= –1

3) k_1,2=±i

4) k_1,2=0

32. Корни характеристического уравнения k²+k+1=0, равны

1) k_1,2=1

2) k_1,2= –1

3) k_1,2=±i

4) k_1,2=0

33. Общим решением дифференциального уравнения y′′+y=0 является уравнение:

1)

2)

3)

4)

34. Общим решением дифференциального уравнения y′′–y′+y=0 является

1)

2)

3)

4)

35. Общим решением дифференциального уравнения y′′=e^3x является

1)

2)

3)

4)

36. Скорость охлаждения тела описывается дифференциальным уравнением

1)

2)

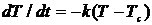
3)

4)

37. Седиментация твердых частиц в жидкости описывается дифференциальным уравнением

1)

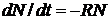
2)

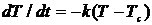
3)

4)

38. Закон растворения лекарственных форм вещества из таблеток, описывается дифференциальным уравнением

1)

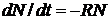
2)

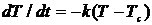
3)

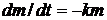
4)

39. Закон размножения бактерий с течением времени, описывается дифференциальным уравнением

1)

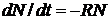
2)

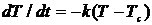
3)

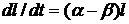
4)

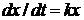
40. Закон роста клеток с течением времени, описывается дифференциальным уравнением

1)

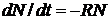
2)

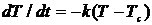
3)

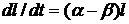
4)

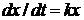
41. Закон разрушения клеток в звуковом поле, описывается дифференциальным уравнением

1)

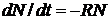
2)

3)

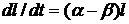
4)

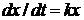
42. Закон изменения числа незараженных особей с течением времени, описывается дифференциальным уравнением

1)

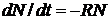
2)

3)

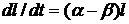
4)

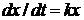
43. Охлаждение тела с течением времени происходит по закону

1)

2)

3)

4)

44. Растворение лекарственных форм вещества из таблеток происходит по закону

1)

2)

3)

4)

45. Разрушение клеток в звуковом поле происходит по закону

1)

2)

3)

4)

46. Рост клеток с течением времени происходит по закону

1)

2)

3)

4)

47. Убывание числа незараженных особей с течением времени происходит по закону

1)

2)

3)

4)

48. Увеличение количества бактерий с течением времени происходит по закону

1)

2)

3)

4)

49. Постоянная скорости растворения вещества из таблеток определяется по формуле

1)

2)

3)

4)

50. Скорость оседания частиц в жидкости находится из уравнения

1)

2)

3)

4)

51. Предельная скорость оседания частиц в жидкости (t→¥) определяется по формуле

1)

2)

3)

4)

52. Предельная скорость оседания частицы массой 1г в жидкости с коэффициентом трения 0,2 равна

1) 0,2

2) 0,14

3) 1,4

4) 7

53. За 1 час количество лекарственного вещества в таблетке уменьшилось в е раз. Постоянная скорость растворения лекарственного вещества равна

1) 1

2) 0

3) е

4) ln2

54. За 1 час количество лекарственного вещества в таблетке уменьшилось в 2 раза. Постоянная скорость растворения лекарственного вещества равна

1) 1

2) 0

3) е

4) ln2

55. В начальный момент времени число незараженных особей равно числу зараженных и равно 50. Коэффициент пропорциональности равен 0,1. Тогда число незараженных особей убывает по закону

1)

2)

3)

4)

56. Начальная концентрация суспензии клеток в звуковом поле равна 100. Коэффициент пропорциональности равен 0,2. Разрушение клеток в звуковом поле с течением времени описывается уравнением

1)

2)

3)

4)

57. Рост клеток с течением времени изображен на рисунке

1)

2)

3)

4)

58. Изменение числа клеток в постоянном звуком поле изображено на рисунке

1)

2)

3)

4)

59. Увеличение количества бактерий с течением времени изображено на рисунке

1)

2)

3)

4)

60. популяция бактерий x(t) растет так, что скорость ее роста в момент времени t составляет половину от размера популяции. Начальный размер популяции равен 100. Закон роста популяции описывается уравнением

1) x(t)=100e^0,5t

2) x(t)=0,5e^100t

3) x(t)=50e^t

4) x(t)=0,5(100–t)

61. Если в начальный момент времени температура тела равна 100° С, а температура окружающего воздуха 20° С, то скорость охлаждения тела описывается уравнением

1) Т=100+80е^-кt

2) Т=20+80е^-кt

3) Т=100+20е^-кt

4) Т=80+20е^-кt

Выберите правильные ответы

62. Дифференциальное уравнение содержит

1) аргумент

2) функцию

3) производную

4) первообразную

63. Однородное дифференциальное уравнение 1 порядка решается с помощью замены переменной

1) u=yx

2) y=ux

3) u=y/x

4) u=y+x

64. Производную функции y′ в однородном дифференциальном уравнении 1 порядка можно заменить выражением

1) u′x+u

2) u′+ux

3)

4)

65. Константу C в общем решении дифференциального уравнения можно заменить выражением

1) С²

2) е^С

3) lnC

4) xC