Всего проведено n наблюдений ( объем выборки равен n ).
 |
Если данные наблюдений нанести на координатную плоскость, получим корреляционное поле:
 |
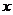При исследовании двух факторов этот построенный график уже показывает, существует зависимость или нет, характер этой зависимости. В частности, на приведенном графике уже видно, что с ростом фактора x значение фактора y тоже увеличивается. Правда зависимость эта нечеткая, размытая, или, правильно говоря, статистическая.
Определение:
Корреляционной зависимостью y от x называют функциональную зависимость среднего значения y ( т.е.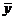 
) от х :
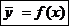( 1 )
Уравнение ( 1 ) называют уравнением регрессии y на x;
функцию 
называют функцией регрессии y на x;
ее график -- линией регрессии y на x .
При помощи уравнений регрессии может осуществляться, например, изучение взаимовлияния экономических переменных.
Уравнение регрессии — формула статистической связи между случайными переменными.
Если формула линейная, то говорят о линейной регрессии, если нелинейная — о нелинейной регрессии.
Формула статистической взаимосвязи между двумя переменными называются парной регрессией.
Если же формула статистической взаимосвязи выражается более чем двумя переменными, то речь идет о множественной регрессии (линейной, нелинейной).
Кейнсом была предложена линейная формула зависимости частного потребления от имеющегося дохода.
При статистическом исследовании соответствующих переменных, на первом этапе всегда осуществляется выбор формы взаимосвязи между переменными. Такой подход позволяет реализовать этап (параметризации) структуризации уравнений регрессии. На этом этапе Кейнс остановился на линейной модели. Однако регрессионый анализ решает две основные задачи.
Задачи регрессионного анализа:
1. Спецификация математической модели, т.е. выбор и обоснование аналитической зависимости между переменными. На этом этапе всегда получают уравнение регрессии.
В то же время, пока уравнение регрессии не будет соответствующим образом оценено, не будет проведен этап исследования его адекватности, уравнение регрессии будет представлять собой всего лишь гипотезу.
2. Статистический анализ уравнения регрессии. Этап проводится с целью определения адекватности уравнения регрессии и установления значимого влияния независимой переменной на зависимую. Этот этап называется этапом параметризации уравнения регрессии.
На первом этапе исследования решают задачу спецификации уравнения регрессии. Для парной регрессии такая задача решается на основе соответствующего корреляционного поля.
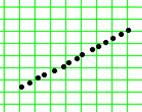
В зависимости от того, какое уравнение выбирается, регрессия получает соответствующее название:
|
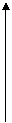y
|
x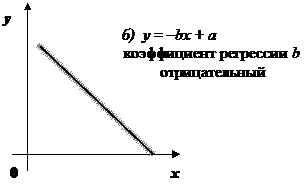 
А так же парные нелинейные регрессии:
 |
 |
 |
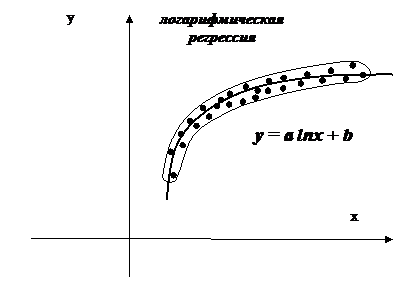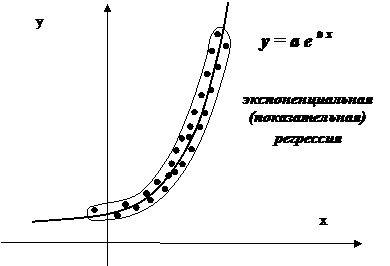Парная линейная регрессия