Линия, нагруженная на реактивное сопротивление

В данном случае сопротивление нагрузки Z_н=jX_н, а напряжение в конце линии U_н= I_н jX_н.

Уравнения линии:

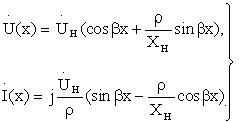
Введя множитель 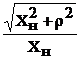и полагая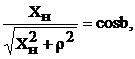 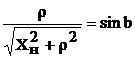, получаем ,

,

,

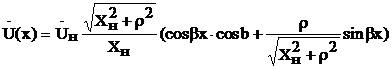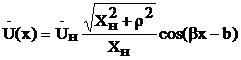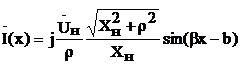где .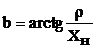

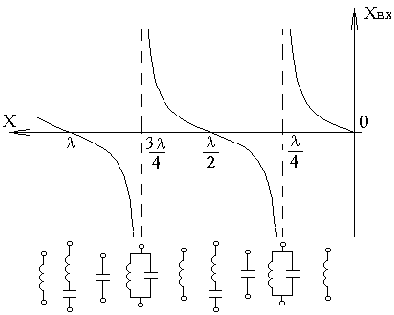
Рис.10

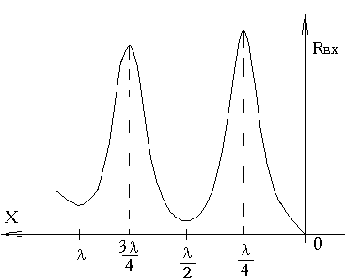
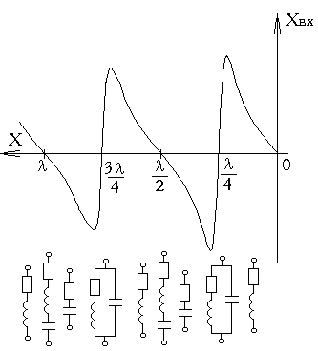
Рис.11

Мгновенные значения напряжения и тока в линии

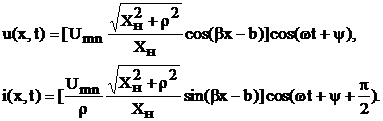
Из последних выражений следует:

1) линия, замкнутая на реактивное сопротивление, работает в режиме стоячих волн;

2) амплитудные значения напряжения и тока в 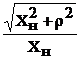раз больше, чем в разомкнутой линии;

3) узлы напряжения находятся в точках, где сos(bx-b)=0, т.е. 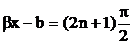, 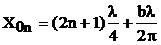; узлы тока, определяются из условия sin(bx-b)=0, т.е. .

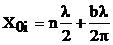Если линия нагружена на емкостное сопротивление ( 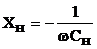), то

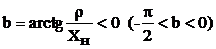и узлы напряжения смещаются относительно точек 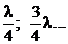вправо к нагрузке (рис.12).

Очевидно, С_Н может быть заменена отрезком разомкнутой линии 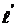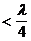. Для расчета 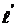имеем 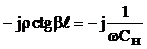, откуда .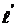

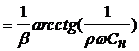Если линия нагружена на индуктивное сопротивление (X_Н=wL_Н>0), то узлы напряжения будут располагаться слева от точек 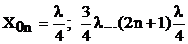(рис.13).

Поскольку входное сопротивление короткозамкнутой линии длиной 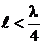имеет индуктивный характер, всегда можно подобрать такой добавочный отрезок 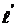, входное сопротивление которого было бы равно X_Н=wL_Н. Для расчета 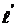имеем 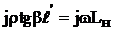,откуда .

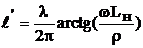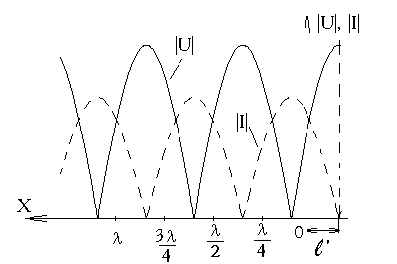
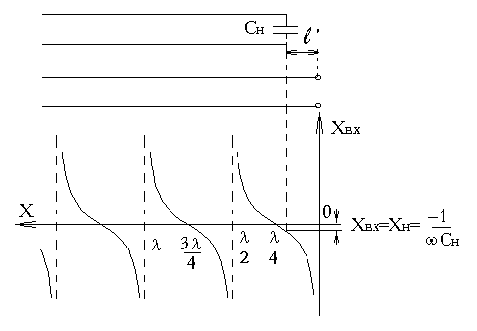
Рис.12

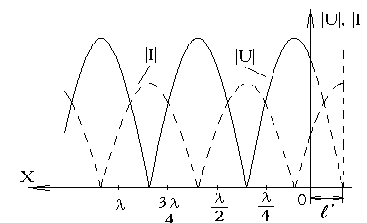
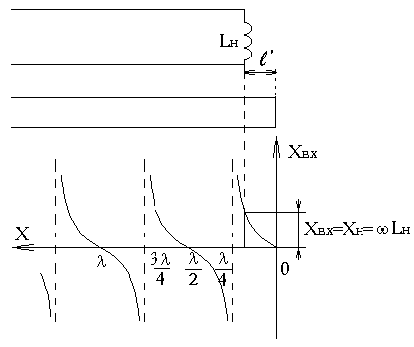
Рис.13

Режим смешанных волн

В линии без потерь, нагруженной на активное сопротивление, не равное волновому 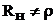, или комплексное сопротивление, устанавливается режим смешанных волн. Отсутствие согласования приводит к появлению отражённой волны, амплитуда которой меньше амплитуды падающей волны благодаря потреблению мощности сопротивлением нагрузки R_Н.

Для линии без потерь, нагруженной на 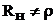, 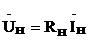и ), ).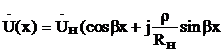

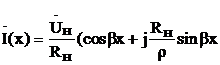Для амплитуд напряжения и тока имеем

,

.

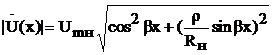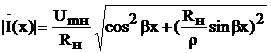Характер распределения амплитуд напряжения и тока вдоль линии определяется соотношением между сопротивлением нагрузки и волновым сопротивление линии.

На рис.14 приведены графики распределения напряжения и тока в линии при .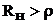

Максимумы напряжения и тока чередуются через расстояния 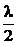. Очевидно, минимальные значения тока и напряжения могут быть представлены бегущей волной тока и напряжения, а максимальные - как сумма бегущей и стоячей волн: .

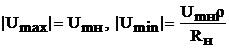По мере увеличения сопротивления нагрузки |Umin| и |Imin| будут уменьшаться, в пределе при 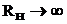обращаясь в нуль, что означает вырождение смешанных волн в стоячие. При уменьшении R_Н ( 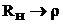) стоячие волны уменьшаются и режим смешанных волн стремится к режиму бегущих волн.

Для оценки степени близости режима смешанных волн к режиму бегущих волн вводится коэффициент бегущей волны (КБВ);

.

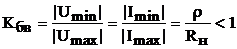Величина, обратная КБВ, получила название коэффициента стоячей волны КСВ;

.

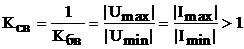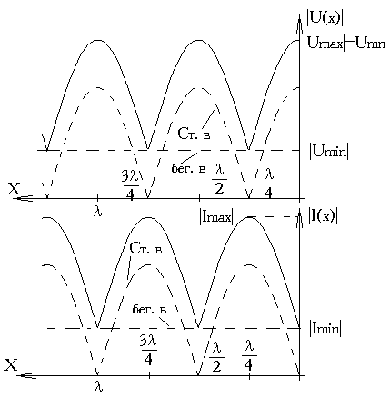
Рис.14

Степень согласования линии с нагрузкой оценивают также коэффициентом отражения. Различают коэффициент отражения по напряжению как отношение напряжения отражённой волны к напряжению падающей волны 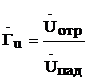и коэффициент отражения по току .

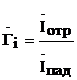Выше было показано, что

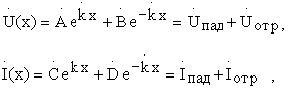
тогда

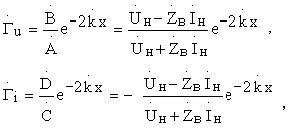
т.е. 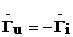, при x=0 .

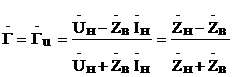Очевидно, коэффициент отражения жестко связан с Кбв и Ксв.

Действительно

.

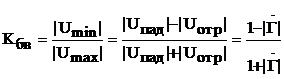Если линия нагружена на сопротивление R_Н<r, то графики распределения напряжения и тока вдоль линии аналогичны предыдущим, однако на конце линии теперь имеет место минимум напряжения и максимум тока. Коэффициент бегущей волны в этом случае 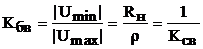.