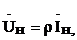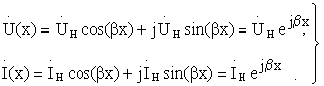Исследование цепей с распределёнными параметрами

ИССЛЕДОВАНИЕ ЦЕПЕЙ С РАСПРЕДЕЛЁННЫМИ ПАРАМЕТРАМИ

Цель работы: экспериментально исследовать распределение напряжения вдоль однородной длинной линии при различных сопротивлениях нагрузки.

Общие сведения

В современной радиотехнике всё более широкое применение находят устройства, геометрические размеры которых соизмеримы или больше длины волны распространяющихся в них электромагнитных колебаний. Например, рассматривая передачу электромагнитной энергии в линиях связи, фидере, волноводе, антенне и т.п., следует учитывать, что магнитные и электрические поля распределены по всей длине этих устройств, и превращение электромагнитной энергии в тепло также происходит по всей длине устройств. Такие цепи характеризуются распределёнными по всей длине индуктивностями, ёмкостями, активными сопротивлениями и называются цепями с распределёнными параметрами. Воздействие генератора на такую цепь проявляется в некоторой точке цепи не мгновенно, а с запаздыванием на время, определяемое длиной пути тока между генератором и этой точкой и скоростью распространения колебаний в цепи. Поэтому мгновенное значение тока в реальной цепи с конечными размерами принципиально не может быть везде одинаково.

Простейшими цепями с распределёнными параметрами являются длинные линии (двухпроводные воздушные линии связи, симметричные и коаксиальные кабельные линии проводных систем связи, полосковые линии передачи и т.п., имеющие длину l ,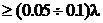

l- длина волны электромагнитных колебаний).

Линии передачи, геометрическая конфигурация, а также свойства материалов (проводников и диэлектриков), которых остаются неизменными по всей длине, называются однородными, или регулярными.

Рассмотрим в качестве примера двухпроводную линию передачи с известным сопротивлением нагрузки на конце (рис.1).

Электромагнитные свойства такой линии характеризуются первичными параметрами, т.е. параметрами, отнесёнными к единице длины линии:

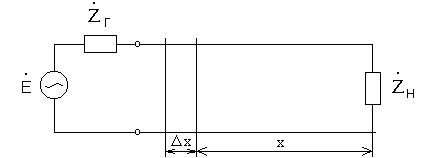
Рис.1

Строгое решение задачи о зависимости тока в линии от времени и координаты х может быть получено из системы уравнений Максвелла. Однако этот метод имеет существенный недостаток, заключающийся в том, что решение системы уравнений Максвелла удаётся довести до конца только для ограниченного класса линий передачи с достаточно простой конфигурацией.

Если же представить длинную линию в виде отрезков длиной DX<<l каждый, то в пределе при DX®0 такие малые элементы линии могут быть описаны методами, принятыми в теории цепей. В этом случае любой малый отрезок линии можно представить в виде эквивалентной схемы (рис.2), состоящей из сосредоточенных малых элементов DL=L₁×DX, DC=C₁×DX, DR= R₁×DX, Dg= g₁×DX.

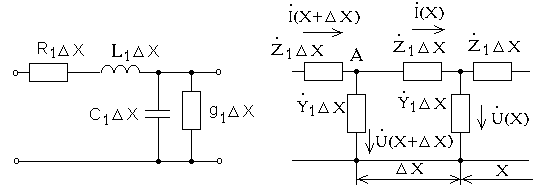
Рис.2 Рис.3

Вся же линия может быть представлена каскадным соединением элементарных четырёхполюсников (рис.3), где Z₁= R₁+jwL₁ - погонное комплексное сопротивление, Y₁= g₁+jwC₁ - погонная комплексная проводимость.

Обозначив символами 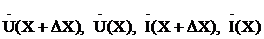комплексные амплитуды напряжений и токов соответственно на входе и выходе элементарного четырёхполюсника для внутреннего контура и узла Ана основании второго и первого законов Кирхгофа, получим тождества

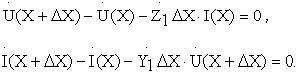
С точностью до малых величин второго порядка

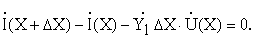
Представим последние тождества системой разностных уравнений:

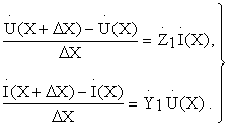
Совершая предельный переход при 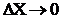, получим систему двух дифференциальных уравнений с постоянными коэффициентами, которые называются телеграфными уравнениями

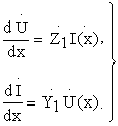
Если продифференцировать обе части телеграфных уравнений по х, то последняя система может быть сведена к двум дифференциальным уравнения второго порядка как относительно напряжения, так и относительно тока:

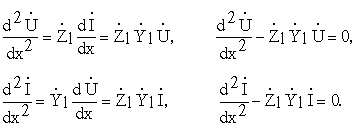
В теории волновых процессов эти уравнения носят названиеуравнений Гельмгольца, их общее решение записывается следующим образом:

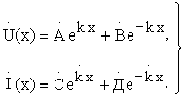
где 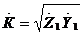- комплексный коэффициент распространения.

Первые слагаемые в выражениях для напряжения и тока определяют комплексные амплитуды падающих волн, а вторые - отраженных волн напряжения и тока.

Постоянные интегрирования определяются из начальных условий:

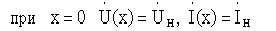
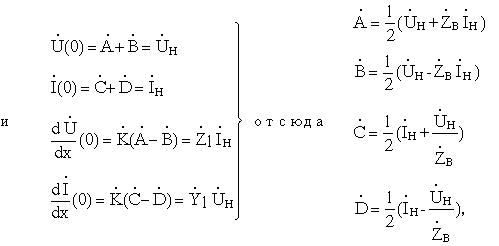
где 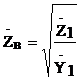- волновое сопротивление линии.

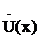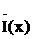Подставив постоянные интегрирования в уравнения для и , получим

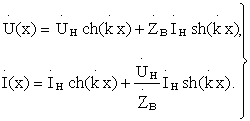
Для линии без потерь R₁=g₁=0, 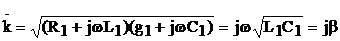, где b - фазовая постоянная, показывающая отставание фазы колебаний за время их распространения на единице длины.

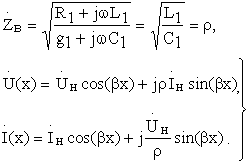
В зависимости от соотношения сопротивления нагрузки и волнового сопротивления линия работает в режиме бегущих волн, стоячих или смешанных волн.

I. Режим бегущих волн

Бегущие волны получаются в том случае, когда линия нагружена на сопротивление, равное волновому.

Для линии без потерь R_н=r,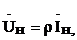

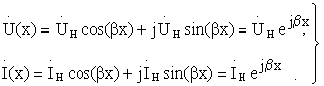
Действительно,

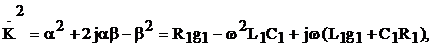
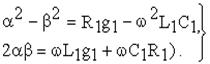
Совместное решение этой системы:

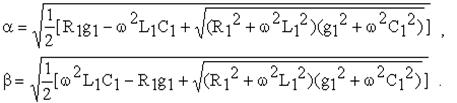
В рабочем диапазоне частот 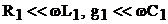и a изменяется в пределах от 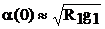до 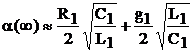(рис.4).

bнеограниченно растёт при увеличении частоты.

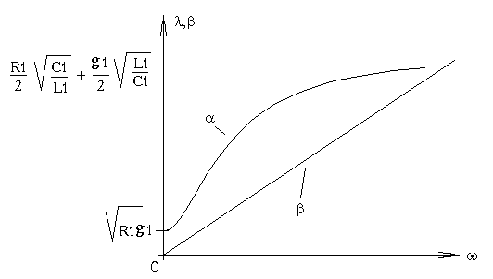
Рис.4

Учитывая, что проводимость утечки , .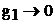

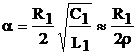Волновое сопротивление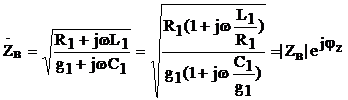

при w=0 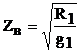, при .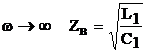

Поскольку в реальной линии 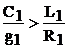, то реактивная составляющая волнового сопротивления имеет ёмкостный характер (рис.5).

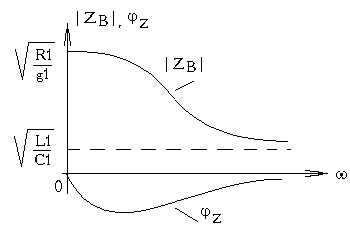
Рис.5

Для получения режима бегущих волн в линии с потерями необходимо иметь .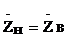

Тогда

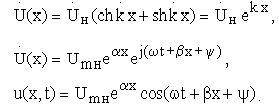
Ток в линии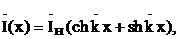

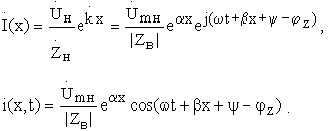
Амплитуды напряжения и тока в начале линии 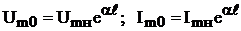, где l - длина линии, отсюда

.

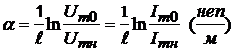Таким образом, в линии с потерями амплитуды напряжения и тока уменьшаются при увеличении длины линии (рис.6).

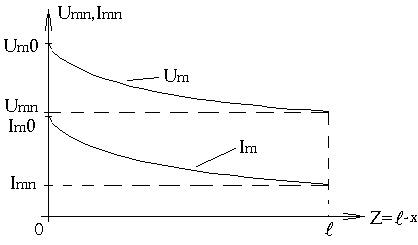
Рис.6

Следует отметить, что ток опережает напряжение на угол j_z, определяемый реактивной составляющей волнового сопротивления.

Режим стоячих волн

Стоячие волны в линии передачи возникают в трёх случаях:

а) линия разомкнута на конце;

б) линия замкнута накоротко;

в) линия нагружена на реактивное сопротивление (L или C).

2.1. Разомкнутая линия

В режиме холостого хода передачи энергии в нагрузку нет, поскольку в разомкнутой на конце линии нет тока, следовательно, вся энергия отражается от конца линии и возвращается к генератору, устанавливая в линии режим стоячих волн как совокупность падающей и отражённой волн.

Короткозамкнутая линия

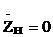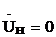В линии в режиме короткого замыкания и , поэтому уравнения линии имеют вид

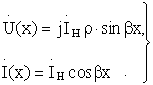
Мгновенные значения напряжения и тока

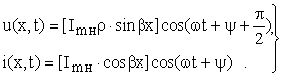
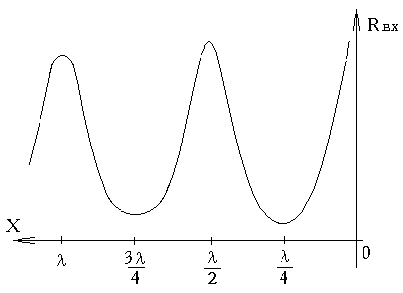
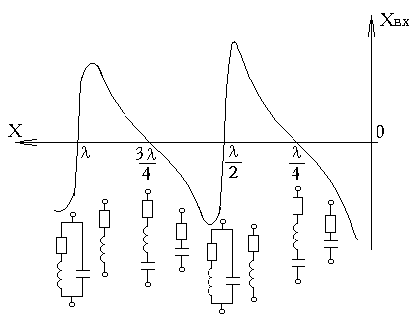
Рис.9

Полученные выражения показывают, что, как и в разомкнутой линии, имеют место стоячие волны. Однако имеются следующие отличия:

1) распределение напряжения вдоль линии пропорционально sinbx, а тока -cosbx;

2) в каждой точке линии напряжение опережает ток на 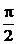, а не отстаёт, как в разомкнутой линии;

3) входное сопротивление ;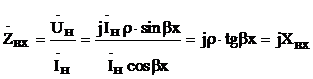

для линии с потерями .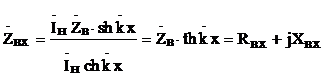

Графики изменения реактивной и активной составляющих входного сопротивления от длины линии приведены на рис.10 (линия без потерь) и рис.11 (линия с потерями).

Режим смешанных волн

В линии без потерь, нагруженной на активное сопротивление, не равное волновому 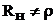, или комплексное сопротивление, устанавливается режим смешанных волн. Отсутствие согласования приводит к появлению отражённой волны, амплитуда которой меньше амплитуды падающей волны благодаря потреблению мощности сопротивлением нагрузки R_Н.

Для линии без потерь, нагруженной на 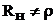, 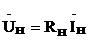и ), ).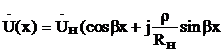

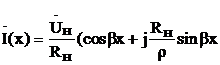Для амплитуд напряжения и тока имеем

,

.

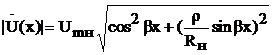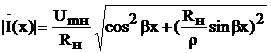Характер распределения амплитуд напряжения и тока вдоль линии определяется соотношением между сопротивлением нагрузки и волновым сопротивление линии.

На рис.14 приведены графики распределения напряжения и тока в линии при .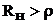

Максимумы напряжения и тока чередуются через расстояния 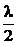. Очевидно, минимальные значения тока и напряжения могут быть представлены бегущей волной тока и напряжения, а максимальные - как сумма бегущей и стоячей волн: .

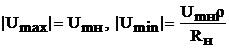По мере увеличения сопротивления нагрузки |Umin| и |Imin| будут уменьшаться, в пределе при 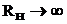обращаясь в нуль, что означает вырождение смешанных волн в стоячие. При уменьшении R_Н ( 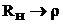) стоячие волны уменьшаются и режим смешанных волн стремится к режиму бегущих волн.

Для оценки степени близости режима смешанных волн к режиму бегущих волн вводится коэффициент бегущей волны (КБВ);

.

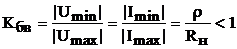Величина, обратная КБВ, получила название коэффициента стоячей волны КСВ;

.

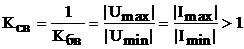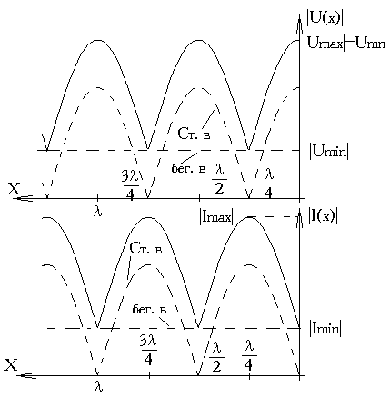
Рис.14

Степень согласования линии с нагрузкой оценивают также коэффициентом отражения. Различают коэффициент отражения по напряжению как отношение напряжения отражённой волны к напряжению падающей волны 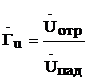и коэффициент отражения по току .

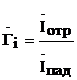Выше было показано, что

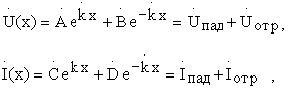
тогда

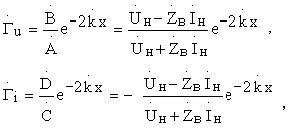
т.е. 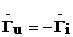, при x=0 .

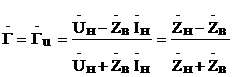Очевидно, коэффициент отражения жестко связан с Кбв и Ксв.

Действительно

.

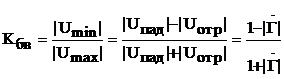Если линия нагружена на сопротивление R_Н<r, то графики распределения напряжения и тока вдоль линии аналогичны предыдущим, однако на конце линии теперь имеет место минимум напряжения и максимум тока. Коэффициент бегущей волны в этом случае .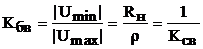

Содержание отчёта

1. Результаты выполнения домашнего задания в виде таблиц.

2. Схема измерений.

3. Результаты выполнения лабораторного задания в виде таблиц.

4. Графики по результатам домашнего и лабораторного заданий.

5. Результаты обработки экспериментальных данных.

6. Краткие выводы.

3.5. Контрольные вопросы

1. Каков физический смысл первичных параметров линии?

2. Как определить первичные параметры по результатам эксперимента?

3. Что такое вторичные параметры линии? Каков их физический смысл?

4. Как определить вторичные параметры линии?

5. Нарисовать и объяснить распределение тока и напряжения в линии для случаев:

а) разомкнутая линия;

б) замкнутая линия;

в) реактивная нагрузка ёмкостного характера;

г) реактивная нагрузка индуктивного характера;

д) согласованная нагрузка;

е) активная нагрузка Rн>Zв;

ж) активная нагрузка Rн<Zв.

6. Объяснить принцип работы четвертьволнового шлейфа.

7. Как экспериментально определить коэффициенты отражения, бегущей и стоячей волн?

8. Нарисовать зависимость активной и реактивной составляющих входного сопротивления линии, нагруженной на одно из сопротивлений (см. вопрос 5, а-ж).

9. Нарисовать распределение тока и напряжения в линии с потерями для случая комплексной нагрузки.

10. Каким образом обеспечивается режим бегущей волны в линии при несогласованной нагрузке на её конце?

Литература

1. Атабеков Р.И. Основы теории цепей. М.: Энергия, 1969.

2. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. Л.: Энергия, 1972.

2. Попов В.П. Основы теории цепей. М.: Высш. шк., 1985.

4. Добротворский И.Н. Лабораторный практикум по основам теории цепей. М.: Высш. Шк., 1986.

5. Баканов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических цепей и электроники. М.: Радио и связь.

6. Лосев А.К. Линейные радиотехнические цепи. - М.: Высш. шк., 1971.

7. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. - М.: Высш. шк., 1972.

8. Теория линейных электрических цепей/Б.П. Афанасьев, О.Е. Гольдин, И.Г. Кляцкин, Г.Я. Пинес и др. М.: Высш. шк., 1973.

9. Лосев А.К. Теория линейных электрических цепей. М.: Высш. шк., 1987.

10. Добротворский И.Н. Теория электрических цепей. М.:Радио и связь, 1989.

11. Баскаков С.И. Радиотехнические цепи с распределёнными параметрами. М.: Высшая шк., 1980.

12. Калашников А.М., Степук Я.В. Основы радиотехники и радиолокации. М.: Военное издательство Министерства Обороны СССР, 1950.

ИССЛЕДОВАНИЕ ЦЕПЕЙ С РАСПРЕДЕЛЁННЫМИ ПАРАМЕТРАМИ

Цель работы: экспериментально исследовать распределение напряжения вдоль однородной длинной линии при различных сопротивлениях нагрузки.

Общие сведения

В современной радиотехнике всё более широкое применение находят устройства, геометрические размеры которых соизмеримы или больше длины волны распространяющихся в них электромагнитных колебаний. Например, рассматривая передачу электромагнитной энергии в линиях связи, фидере, волноводе, антенне и т.п., следует учитывать, что магнитные и электрические поля распределены по всей длине этих устройств, и превращение электромагнитной энергии в тепло также происходит по всей длине устройств. Такие цепи характеризуются распределёнными по всей длине индуктивностями, ёмкостями, активными сопротивлениями и называются цепями с распределёнными параметрами. Воздействие генератора на такую цепь проявляется в некоторой точке цепи не мгновенно, а с запаздыванием на время, определяемое длиной пути тока между генератором и этой точкой и скоростью распространения колебаний в цепи. Поэтому мгновенное значение тока в реальной цепи с конечными размерами принципиально не может быть везде одинаково.

Простейшими цепями с распределёнными параметрами являются длинные линии (двухпроводные воздушные линии связи, симметричные и коаксиальные кабельные линии проводных систем связи, полосковые линии передачи и т.п., имеющие длину l ,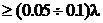

l- длина волны электромагнитных колебаний).

Линии передачи, геометрическая конфигурация, а также свойства материалов (проводников и диэлектриков), которых остаются неизменными по всей длине, называются однородными, или регулярными.

Рассмотрим в качестве примера двухпроводную линию передачи с известным сопротивлением нагрузки на конце (рис.1).

Электромагнитные свойства такой линии характеризуются первичными параметрами, т.е. параметрами, отнесёнными к единице длины линии:

Рис.1

Строгое решение задачи о зависимости тока в линии от времени и координаты х может быть получено из системы уравнений Максвелла. Однако этот метод имеет существенный недостаток, заключающийся в том, что решение системы уравнений Максвелла удаётся довести до конца только для ограниченного класса линий передачи с достаточно простой конфигурацией.

Если же представить длинную линию в виде отрезков длиной DX<<l каждый, то в пределе при DX®0 такие малые элементы линии могут быть описаны методами, принятыми в теории цепей. В этом случае любой малый отрезок линии можно представить в виде эквивалентной схемы (рис.2), состоящей из сосредоточенных малых элементов DL=L₁×DX, DC=C₁×DX, DR= R₁×DX, Dg= g₁×DX.

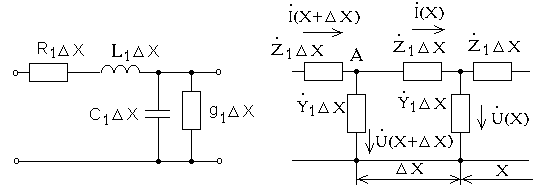
Рис.2 Рис.3

Вся же линия может быть представлена каскадным соединением элементарных четырёхполюсников (рис.3), где Z₁= R₁+jwL₁ - погонное комплексное сопротивление, Y₁= g₁+jwC₁ - погонная комплексная проводимость.

Обозначив символами 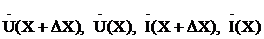комплексные амплитуды напряжений и токов соответственно на входе и выходе элементарного четырёхполюсника для внутреннего контура и узла Ана основании второго и первого законов Кирхгофа, получим тождества

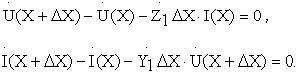
С точностью до малых величин второго порядка

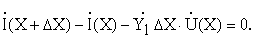
Представим последние тождества системой разностных уравнений:

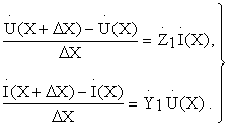
Совершая предельный переход при 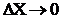, получим систему двух дифференциальных уравнений с постоянными коэффициентами, которые называются телеграфными уравнениями

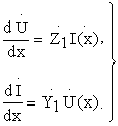
Если продифференцировать обе части телеграфных уравнений по х, то последняя система может быть сведена к двум дифференциальным уравнения второго порядка как относительно напряжения, так и относительно тока:

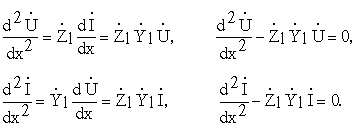
В теории волновых процессов эти уравнения носят названиеуравнений Гельмгольца, их общее решение записывается следующим образом:

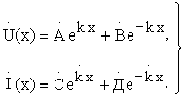
где 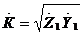- комплексный коэффициент распространения.

Первые слагаемые в выражениях для напряжения и тока определяют комплексные амплитуды падающих волн, а вторые - отраженных волн напряжения и тока.

Постоянные интегрирования определяются из начальных условий:

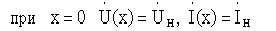
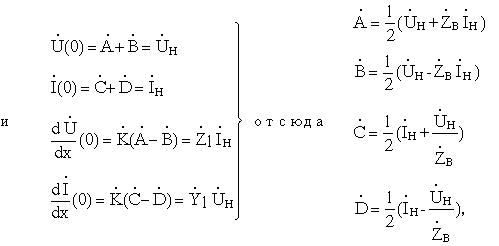
где 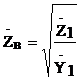- волновое сопротивление линии.

Подставив постоянные интегрирования в уравнения для 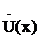и 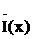, получим

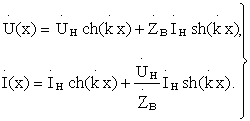
Для линии без потерь R₁=g₁=0, 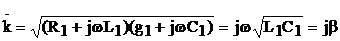, где b - фазовая постоянная, показывающая отставание фазы колебаний за время их распространения на единице длины.

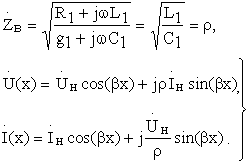
В зависимости от соотношения сопротивления нагрузки и волнового сопротивления линия работает в режиме бегущих волн, стоячих или смешанных волн.

I. Режим бегущих волн

Бегущие волны получаются в том случае, когда линия нагружена на сопротивление, равное волновому.

Для линии без потерь R_н=r,