Лабораторная работа № 3 Принятие решений на основе методов оптимизации
Цель работы: знакомство с постановкой и решением задач оптимизации методами линейного программирования, многокритериальной оптимизации и задачами о смене оборудования.
Содержание работы
Изучите по материалам учебного пособия, лекциям и другим источникам методы линейного программирования, решения задач многокритериальной оптимизации, смены оборудования и проделайте следующую работу.
1. Составьте на свой вкус суточное меню из 4–5 продуктов, исходя из следующих условий: суточная потребность человека в белках – 80 г, в жирах – 100г, углеводах – 360г. Общая калорийность меню для юношей 2700 ккал, для девушек – 2300 ккал. Сформулируйте и решите задачу линейного программирования для определения количества продуктов в двух вариантах:
а) Минимальная стоимость при балансе по белкам, жирам и углеводам и общей калорийности.
б) Минимальный вес продуктов при таком же балансе.
в) Сформулируйте двухкритериальную задачу на основе задач а) и б) и решите ее методом линейной свертки критериев, задавшись весом каждого из критериев.
Примечание Калорийность продуктов найдите в Интернете, а их стоимость – в ближайшем магазине. Для решения задачи используйте программу симплекс-метода, которую тоже можно найти в Интернете.
2. Определите для своего варианта оптимальный срок смены автомобиля по методике учебного пособия (п. 2.5.1) при следующих условиях (время рассчитывается в месяцах):
а) начальная цена автомобиля 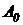 рублей,
рублей,
б) потеря стоимости определяется формулой 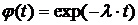 ;
;
в) стоимость обслуживания возрастает по закону 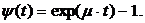
Исходные данные приведены в таблице 3.1.
Таблица 3.1
| № варианта | 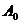 тыс. руб. тыс. руб. | 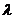 1/мес. 1/мес. | 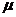 1/мес. 1/мес. |
| 0,05 | 0,03 | ||
| 0,07 | 0,04 | ||
| 0,02 | 0,06 | ||
| 0,03 | 0,02 | ||
| 0,01 | 0,05 | ||
| 0,015 | 0,07 | ||
| 0,017 | 0,065 | ||
| 0,025 | 0,03 | ||
| 0,04 | 0,05 | ||
| 0,06 | 0,015 | ||
| 0,03 | 0,03 | ||
| 0,01 | 0,04 | ||
| 0,015 | 0,06 | ||
| 0,017 | 0,02 | ||
| 0,025 | 0,05 | ||
| 0,01 | 0,065 | ||
| 0,015 | 0,03 | ||
| 0,017 | 0,05 | ||
| 0,025 | 0,015 | ||
| 0,04 | 0,03 | ||
| 0,05 | 0,03 | ||
| 0,07 | 0,04 | ||
| 0,02 | 0,06 | ||
| 0,03 | 0,02 | ||
| 0,01 | 0,05 | ||
| 0,015 | 0,07 | ||
| 0,017 | 0,065 | ||
| 0,025 | 0,03 | ||
| 0,04 | 0,05 | ||
| 0,06 | 0,015 | ||
| г00 | 0,03 | 0,03 | |
| 0,01 | 0,04 | ||
| 0,015 | 0,06 | ||
| 0,017 | 0,02 | ||
| 0,025 | 0,05 |
Содержание отчета по работе
Отчет по лабораторной работе должен содержать:
· Титульный лист с указанием номера группы и исполнителей;
· Для задачи 1 выпишите переменные, ограничения и критерии оптимизации, а также полученные решения для каждого из варианта постановки.
· Для задачи 2 постройте график изменения удельной себестоимости 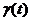 и укажите время, когда эта функция достигает минимума.
и укажите время, когда эта функция достигает минимума.
Лабораторная работа № 4 Вероятностное моделирование динамики систем на основе цепей Маркова с дискретным временем
Цели работы
1. Освоить основные положения теории конечных цепей Маркова (ЦМ) с дискретным временем.
2. Научиться составлять ЦМ для моделирования систем и анализа динамики их функционирования.
3. Научиться вычислять характеристики функционирования ЦМ.
Содержание работы
1) Изучить теоретический материал по ЦМ по учебному пособию
(глава 3), по лекциям или другим источникам.
2) Для заданного варианта модели системы составить матрицу переходных вероятностей.
3) Вычислить с помощью пакета MathCad или специально написанной программы векторы вероятностей X(t)пребывания системы в каждом из состояний для 15 шагов при старте из заданного входного состояния и построить соответствующие графики.
4) Структурировать матрицу 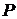 , выделить множества невозвратных и эргодических состояний
, выделить множества невозвратных и эргодических состояний 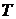 и
и 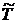 . Выписать матрицы
. Выписать матрицы 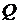 ,
, 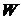 ,
, 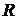 .
.
5) Определить среднее число тактов пребывания процесса в каждом из невозвратных состояний путем вычисления матрицы 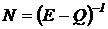 .
.
6) На основе матрицы 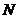 вычислить среднюю трудоемкость процесса
вычислить среднюю трудоемкость процесса 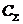 .
.
7) Оценить среднеквадратичное отклонение от среднего числа пребываний процесса в множестве невозвратных состояний 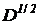 , где
, где 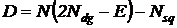 и соответствующее среднеквадратичное отклонение трудоемкости от среднего
и соответствующее среднеквадратичное отклонение трудоемкости от среднего 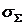 .
.
8) Оценить предельные вероятности пребывания процесса в множестве эргодических состояний:
а) путем прямого возведения матрицы 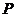 в высокую степень,
в высокую степень,
б) путем спектрального разложения матрицы.
Содержание отчета по работе
Отчет по лабораторной работе должен содержать:
· титульный лист с указанием исполнителя и номера варианта,
· исходные данные по ЦМ – граф смены состояний, матрицы переходных вероятностей 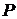 ;
; 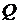 ,
, 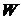 и вектор начальных условий X(0),
и вектор начальных условий X(0),
· таблицу векторов X(t), t=0,1,…15, полученных по формуле 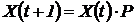 и графики
и графики 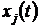 , j=1,…n, t=0,…15;
, j=1,…n, t=0,…15;
· матрицу средних значений 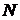 и оценку средней трудоемкости процесса
и оценку средней трудоемкости процесса 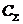 ,
,
· матрицу дисперсий 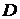 и оценку среднеквадратичного отклонения трудоемкости
и оценку среднеквадратичного отклонения трудоемкости 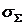 ,
,
· оценки предельных вероятностей пребывания процесса в состояниях эргодического множества, вычисленные:
а) путем прямого возведения матрицы 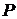 в высокую степень,
в высокую степень,
б) путем спектрального разложения матрицы 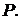
Исходные данные к работе
Исходные данные представлены в виде таблицы 4.1 и набора схем. По указанному преподавателем номеру варианта в таблице выбирается соответствующая строка. Второй столбец таблицы указывает код схемы и стартовое состояние (например, Г1 – схема Г, старт происходит из состояния S1). Далее указаны вероятности перехода между состояниями в десятых долях (т.е. указанное в таблице значение 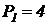 означает, что
означает, что 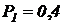 ). Этими вероятностями помечены дуги на схеме. Некоторые дуги не помечены – соответствующие вероятности определяются из условия, что сумма вероятностей на дугах, отходящих от каждого узла, равна единице. Следующая группа столбцов задает трудоемкости отдельных процессов
). Этими вероятностями помечены дуги на схеме. Некоторые дуги не помечены – соответствующие вероятности определяются из условия, что сумма вероятностей на дугах, отходящих от каждого узла, равна единице. Следующая группа столбцов задает трудоемкости отдельных процессов 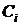 в секундах.
в секундах.
| Таблица 4.1 | mмах 1/с | 0.1 | 1.2 | 0.2 | 0.5 | 1.2 | 2.5 | 10.5 | |||||||||||||
| Трудоемкости, С, c | С7 | - | - | - | - | - | - | - | - | - | - | - | - | ||||||||
| С6 | |||||||||||||||||||||
| С5 | |||||||||||||||||||||
| С4 | |||||||||||||||||||||
| С3 | |||||||||||||||||||||
| С2 | |||||||||||||||||||||
| С1 | |||||||||||||||||||||
| Вероятности переходаРk´10 | Р10 | - | - | - | - | - | - | - | - | ||||||||||||
| Р9 | |||||||||||||||||||||
| Р8 | |||||||||||||||||||||
| Р7 | |||||||||||||||||||||
| Р6 | |||||||||||||||||||||
| Р5 | |||||||||||||||||||||
| Р4 | |||||||||||||||||||||
| Р3 | |||||||||||||||||||||
| Р2 | |||||||||||||||||||||
| Р1 | |||||||||||||||||||||
| Схема, вход | A1 | А2 | Б1 | Б2 | В1 | В2 | Г1 | Г2 | Д1 | Д2 | А1 | А2 | Б1 | Б2 | В1 | В2 | Г1 | Г2 | Д1 | Д2 | |
| № вар. |
| Таблица 4.1(продолжение) | mмах 1/с | 0.1 | 1.2 | 0.2 | ||||||||||||
| Трудоемкости, С, c | С7 | - | - | - | - | - | - | - | - | |||||||
| С6 | ||||||||||||||||
| С5 | ||||||||||||||||
| С4 | ||||||||||||||||
| С3 | ||||||||||||||||
| С2 | ||||||||||||||||
| С1 | ||||||||||||||||
| Вероятности переходаРk´10 | Р10 | - | - | - | - | |||||||||||
| Р9 | ||||||||||||||||
| Р8 | ||||||||||||||||
| Р7 | ||||||||||||||||
| Р6 | ||||||||||||||||
| Р5 | ||||||||||||||||
| Р4 | ||||||||||||||||
| Р3 | ||||||||||||||||
| Р2 | ||||||||||||||||
| Р1 | ||||||||||||||||
| Схема, вход | A1 | А2 | Б1 | Б2 | В1 | В2 | Г1 | Г2 | Д1 | Д2 | А1 | А2 | Б1 | Б2 | В1 | |
| № вар. |
