Обработка опытных данных с помощью интерполирования

Цель: изучить задачи интерполирования; научиться составлять блок-схемы алгоритмов интерполирования и реализовывать их на ЭВМ.

Общие сведения:

Пусть некоторая функция задана таблично, т.е. для x_i заданы значения функции y_i=f(x_i), i=0,1,…,n. Требуется найти аналитическое выражение некоторой функции Р, которая в точках x_i принимала бы значения y_i. В такой постановке задача может иметь бесконечное множество решений или не иметь их совсем.

Для определенности задачи искомую функцию Р выбирают из класса алгебраических многочленов, степень которых должна быть на единицу меньше числа точек x_i. Тогда задача формулируется так.

Для заданных значений y_i=f(x_i), i=0,1,…, n можно построить многочлен n- й степени

,

удовлетворяющий двум условиям:

- в точках x_i, i=0,1,…,n значения многочлена Р_n(x_i) совпадают со значениями заданной функции f(x_i), т.е. Р_n(x_i)= f(x_i) = y_i;

- в любой другой точке x^’Î[x₀; x_n] выполняется приближенное равенство Р(x^’) » f(x^’).

Многочлен Р_n(x) называется интерполяционным многочленом, а точки x₀, x₁, …, x_n - узлами интерполирования.

1) Линейное интерполирование

В простейшем случае при n =1 интерполяционный многочлен имеет вид линейной функции .

Интерполирование многочленом Р₁(x) называется линейным интерполированием.

Пусть неизвестная функция f задана в двух точках:

f(x₀) = y₀ и f(x₁) = y₁ .

График линейной функции Р₁(x) должен проходить через данные точки, поэтому получаем систему уравнений:

Решая ее относительно a₀ и a₁ получим:

.

Интерполяционный многочлен Р₁(x) можно записать также в следующем виде:

.

Следовательно, функцию f можно представить приближенным равенством.

Формула

называется формулой линейного интерполирования.

2) Параболическое интерполирование

Пусть некоторая функция f задана своими значениями в (n+1) узле интерполирования, т.е. f(x_i) = y_i, i=0, 1, …, n. В качестве интерполяционного многочлена берут параболу n-го порядка

.

3) Интерполирование полиномом

Для приближенного вычисления значений функции f в промежуточных точках xÎ[x₀; x_n], x ¹ x_i (i=0,1,…,n)существует интерполяционная формула Лагранжа:

.

При разработке алгоритма формулу Лагранжа представляют в виде:

.

Блок-схема алгоритма приведена на рис.12.1.

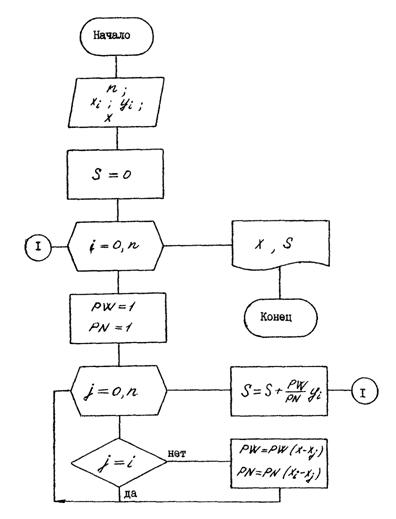
Приняты следующие условные обозначения. Исходные данные: значение n, табличные значения аргументов x_i, функции y_i, а также значения аргумента x, при котором необходимо вычислять функцию f(x); S - частичные суммы интерполяционной формулы Лагранжа, в конечном итоге значение функции f в точке x; PW - произведение множителей числителя одного слагаемого формулы Лагранжа; PN - произведение множителей знаменателя одного слагаемого формулы Лагранжа.

Интерполирование функции с помощью пакета MathСad.

1) линейная интерполяция

linterp(x,y,t) – функция, котораяаппроксимируют данные векторов х и у кусочно-линейной зависимостью (х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания (х₁<x₂<…<x_n); у - вектор действительных данных значений того же размера; t – значение аргумента, при котором вычисляется интерполирующая функция).

Пример линейной интерполяции

2) кубическая сплайн-интерполяция

interp(s,x,y,t) – функция, аппроксимирующая данные векторов х и у кубическими сплайнами (s – вектор вторых производных, созданный одной из сопутствующих функций cspline, pcspline и lcspline; х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; у - вектор действительных данных значений того же размера; t – значение аргумента, при котором вычисляется интерполирующая функция). cspline(x,y) – вектор значений коэффициентов линейного сплайна; pcspline – вектор значений коэффициентов квадратичного сплайна и lcspline – вектор значений коэффициентов кубического сплайна.

Пример кубической сплайн-интерполяции

3) полиномиальная сплайн-интерполяция

interp(s,x,y,t) – функция, аппроксимирующая данные векторов х и у с помощью В-сплайнов; bspline(x,y,u,n) – вектор значений коэффициентов В-сплайна (s – вектор вторых производных, созданный функций bspline; х – вектор действительных данных аргумента, элементы которого расположены в порядке возрастания; у - вектор действительных данных значений того же размера; t – значение аргумента, при котором вычисляется интерполирующая функция; u - вектор значений аргумента, в которых производится сшивка В-сплайнов; n – порядок полиномов сплайновой интерполяции.

Пример интерполяции В-сплайнами

Задание:

1. Изучить методы линейного и параболического интерполирования.

2. Изучить блок-схему алгоритма интерполирования по формуле Лагранжа.

3. Составить блок-схему алгоритма обратного интерполирования по формуле Лагранжа.

4. Составить программу интерполирования функции по формуле Лагранжа для опытных данных (согласовать с преподавателем) и реализовать ее на ПК.

5. Выполнить интерполирование функции различными методами с помощью пакета MathСad.

Контрольные вопросы:

1. Какие основные задачи рассматриваются в теории интерполирования?

2. Опишите постановку задачи интерполирования в общем виде.

3. Что такое интерполяция и экстраполяция? Приведите формулу.

4. Опишите методы интерполирования.

5. Приведите сравнительную характеристику методов интерполирования.

6. Поясните алгоритмы методов интерполирования.

7. Чем оценивается точность функции интерполирования?

8. Поясните программу интерполирования функции по формуле Лагранжа.

9. Как выполнить интерполирование с помощью пакета Mathcad?

Лабораторная работа №13