Теория уравновешивания вращающихся масс
В современном машиностроении применяется большое количество вращающихся звеньев (роторы электродвигателей, турбин, валы и т. д.). Быстроходность машин, а следовательно, и угловые скорости вращающихся звеньев непрерывно растут, поэтому уравновешивание центробежных сил инерции .вращающихся масс имеет важное значение.
Рассмотрим вращающееся звено 1 (рис..1), установленное на своей оси в подшипниках 2. При вращении звена к каждой элементарной точечной массе его будет приложена центробежная сила инерции, направленная по радиусу от оси вращения наружу и равная произведению массы на расстояние ее до оси вращения и на квадрат угловой скорости звена.
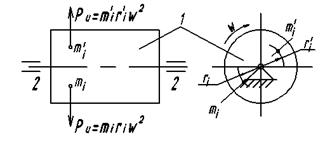
Рис. 1
Если звено 1 будет идеальным телом вращения и ось вращения звена совпадает точно с геометрической осью тела, то такое звено будет полностью уравновешенным. Действительно для каждой массы mi, расположенной на радиусе ri, всегда будет существовать в той же плоскости, но по другую сторону от оси вращения, другая равная ей масса mi’ удаленная от оси на расстояние гi' равное ri. Центробежные силы этих масс взаимно уравновесятся. Поэтому не будет сил, вызывающих дополнительные давления в подшипниках 2 звена. 1. В реальной действительности получить такое идеальное звено невозможно, даже если оно имеет правильную форму тела вращения: нельзя выдержать абсолютно точно за данные размеры и масса звена неоднородна. Во многих случаях форма вращающегося звена (ротора) бывает более сложной, ротор может состоять из нескольких Деталей, положение которых, вследствие неточности сборки, может не соответствовать чертежу. Вследствие этого не все центробежные силы инерции ротора будут уравновешены.
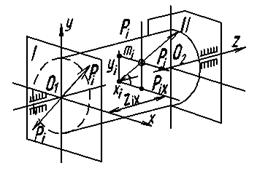
Рис. 2
Рассмотрим ротор 1 (рис. 2), вращающийся в подшипниках 2 с постоянной угловой скоростью w. Проведем две произвольно выбранные плоскости I и II, перпендикулярные оси вращения ротора. Эти плоскости пересекут ось ротора в точках О1 и O2. Зададимся неподвижной системой прямоугольных координат O1XYZ. Начало координат поместим в точке O1, ось O1Z направим вдоль оси вращения ротора, оси O1X и O1Y расположим в .плоскости 1. Возьмем на роторе точку i с неуравновешенной массой mi, положение которой определяется координатами хi yi zi Радиус-вектор этой точки - ri; угол, составленный радиус-вектором с положительным направлением оси ох—ai. Очевидно, что xi=ricosai, yi=riSinai. Центробежная сила инерции Pi, развиваемая массой mi, будет равна:
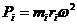 ,
,
Перенесем силу Pi в плоскость 1. Для этого в начале координат O1 приложим две силы, одна из которых равна Pi и ей параллельна, другая равна ей по величине, но противоположна по направлению. В результате получим систему, состоящую из силы, приложенной в точке О1 и пары сил с моментом Mj = PiZi.
Разложим силу Pi и момент пары сил на составляющие по координатным осям,
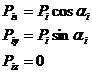
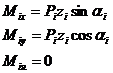
Подставляя в эти равенства значение силы Рi получим:
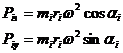
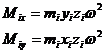
Составляющие части по координатным осям главного вектора сил инерции и главного момента от сил инерции- получим, просуммировав составляющие всех центробежных сил инерции и моментов от центробежных сил инерции отдельных точечно расположенных неуравновешенных масс. Направление векторов моментов выбираем так, что если смотреть вдоль по вектору, момент пары был направлен против часовой стрелки. Тогда
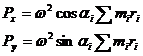 (1)
(1)
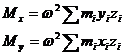 (2)
(2)
Из уравнений 1 и 2 получаем выражения для модулей главного вектора Р и главного момента М.
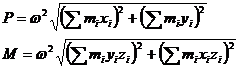 (3)
(3)
Сила Р и момент М вызывают добавочные давления в подшипниках, а от них передаются станине и фундаменту. Эти давления непрерывно изменяют свое направление, так как вектор силы Р и вектор момента М вращаются вместе с ротором. Для того чтобы уничтожить дополнительные давления в опорах и устранить вызываемые ими колебания станин и фундамента, необходимо уравновесить силу Р и момент М, Этот процесс уравновешивания называется балансировкой вращающихся масс (балансировкой ротора).
В некоторых случаях уравновешивается только главный вектор сил инерции Р, а величиной главного момента от пары сил инерции пренебрегают. Это допустимо при малой длине ротора (шестерни, шкивы, маховики) и невысокой угловой скорости вращения его. Такая балансировка называется статической. Обозначим координаты центра тяжести ротора хс и Ус, а всю массу его — mс, тогда мы имеем право записать, что
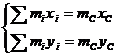 (4)
(4)
Условие, при котором главный вектор сил инерции будет равен нулю, получим, если приравняем нулю проекцию его на оси координат, т. е.
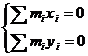
или, имея в виду формулу (4),
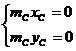 (5)
(5)
откуда вытекает, что главный вектор сил инерции будет равен нулю, если центр тяжести ротора лежит на оси вращения. Обозначим радиус- вектор, определяющий положение центра тяжести ротора, через 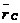 , тогда выражение (5) в векторной форме может быть записано так
, тогда выражение (5) в векторной форме может быть записано так
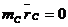 (6)
(6)
Если условие (5) или (6) не будет соблюдено, то необходимо в плоскости приведения 1 (рис.3), которую желательно проводить через центр тяжести ротора, поставить противовес так, чтобы было выдержано условие 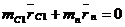
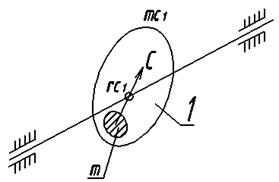
Рис. 3.
Если необходимо произвести полное уравновешивание ротора, то помимо главного вектора сил инерции нужно уравновесить также главный момент от пары сил инерции. Последний может быть представлен парой сил, одну из которых можно расположить в плоскости приведения 1, другую в любой плоскости II. Момент уравновешивающей пары должен быть .равен главному моменту от пары .сил инерции. Уравновешивающие пары сил можно произвести двумя противовесами, расположенными в I и II плоскостях. Таким образом, полное уравновешивание достигается установкой трех противовесов. Однако два из них находятся в одной плоскости I и могут, быть заменены одним противовесом. В итоге задача уравновешивания центробежных сил инерции вращающегося ротора может, быть решена постановкой двух противовесов, расположенные в двух произвольно выбранных плоскостях, перпендикулярных оси вращения ротора. (Следует заметить, что от выбора плоскостей зависят величина противовесов и их расположение в плоскостях приведения).
Условия полной (статической и динамической) уравновешенности ротора получим, если введем в уравнения (1) и (2) центробежные, силы инерции и моменты от центробежных сил двух противовесов. Пусть в плоскости I и II массы противовесов будут mI и mII, положение которых определяется соответственно радиус-векторами rI и rII.
Цель работы
Целью работы является графическое и аналитическое определение величин и расположения противовесов при статическом и динамическом уравновешивании трех известных точечных масс, а также экспериментальная проверка выполненных расчетов.
Пусть имеется ротор (рис. 4), в плоскостях которого 1,2 и 3, перпендикулярных оси вращения, имеются неуравновешенные массы mi, m2. m3. Положения неуравновешенных масс в плоскостях заданы радиус-векторами г1 г2, г3. Положение плоскостей 1, 2 и 3 относительно плоскости приведения X определяется соответственно координатами z1, z2 и z3. Противовесы устанавливаются в плоскости I и плоскости II, расстояние между ними l. Обозначим вес противовеса при статическом уравновешивании через Qп, а радиус-вектор, определяющий положение его центра тяжести, через rп, Тогда условием уравновешенности ротора (здесь массы заменяют их весами) будет:
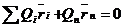 (9)
(9)
При полном уравновешивании ротора веса противовесов устанавливаемых в плоскости I и II, обозначим QI и QII, a радиус-векторы, определяющие положения их центров тяжести, через rI и rII. Тогда условиями полного уравновешивания будут:
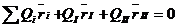 (10)
(10)
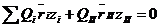 (11)
(11)
При аналитическом решении этой задачи уравнение (9) развернется в два уравнения проекций на оси координат, а уравнение (10) и (11) в четыре уравнения проекций на оси координат.
Совокупность уравнений (10) и (11) является условием полного уравновешенного ротора. Решение этих уравнений сводится к определению весов и положений противовесов и может быть осуществлено аналитически и графически.
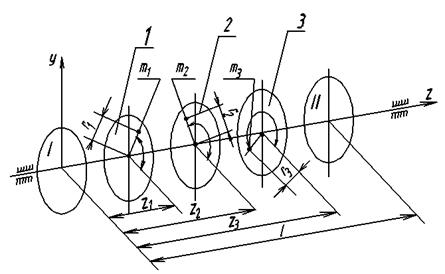
Рис.4
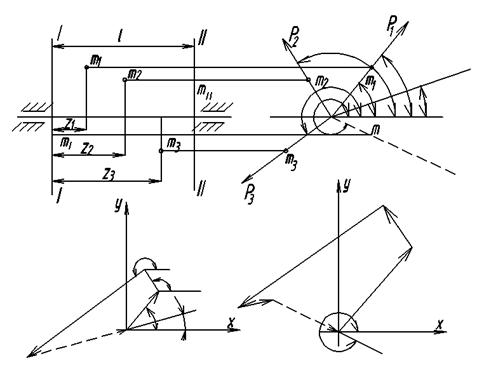
Рис. 5
В обоих случаях сначала решается уравнение (11) и определяются вес и положение противовеса при динамическом уравновешивании. Затем решается уравнение (11).
Более: удобным является графический метод, который заключается в построении векторных многоугольников по уравнениям (10) и (11). Сначала строится векторный многоугольник центробежных моментов инерции по уравнению (11), рис. 5, а. Так как суммарный вектор должен быть равен нулю, то замыкающий вектор многоугольника определяет собой произведение 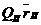 l.
l.
Координата zII известна и равна 1 расстоянию между плоскостями исправления. Из этого произведения можно определить rII, задавшись весом противовеса QII. Угол aII, дающий направление радиуса-вектора противовеса, измеряется по чертежу, затем строится многоугольник по уравнение (10), рис. 5, б. В этом многоугольнике неизвестной величиной будет замыкающий вектор, модуль которого равен QIirI.. Задаваясь QI определяем rI. По чертежу замеряется угол определяющий направление радиуса-вектора противовеса.
Все эти величины, исходя из уравнений (10) и (11), можно вычислить аналитически по соответствующим формулам и сопоставить с результатами графического метода:
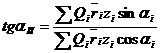 (12)
(12)
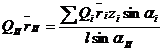 (13)
(13)
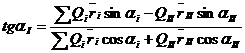 (14)
(14)
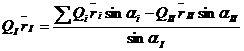 (15)
(15)
Описание установки
| |
| |

| |

| |

| |

| |

| |

| |


| |
| |

| |

| |



Общий вид установки ТММ-35 представлен на рис.. 6.
Рис. 6.
На чугунном основании II закреплены стойки 10 и 18. В стойках закреплены шариковые подшипники вала ротора. На валу ротора установлено пять дисков 2. В крайних дисках (I и II) располагаются противовесы. Три средних диска служат для установки неуравновешенных грузов. Шарикоподшипник правого конца вала I установлен в корпусе 4, который на миниатюрных шарикоподшипниках 6 может перемещаться в горизонтальном направлении по планке 7. Корпус, 4 оттягивается в разные стороны пружинами 8, закрепленными другими концами на кронштейнах 5 при помощи винтов с гайками 9. Если правый конец ротора слегка отвести в сторону и отпустить, то он начнет совершать колебания в горизонтальной плоскости вокруг левой опоры. Разгон ротора осуществляется двигателем 13, закрепленным на рычаге 15. При нажиме вниз на шариковую рукоятку рычага 15, последний, поворачиваясь на оси кронштейна 20, поднимает двигатель 13 вверх и прижимает обрезиненный ролик вала двигателя к фрикционному колесу, закрепленному на валу ротора. Одновременно рычаг 15 освобождает кнопочный контакт, включающий двигатель в работу. Если отпустить шаровую рукоятку рычага 15, то под действием собственного веса двигатель опустится вместе с рычагом 15 вниз, причем ролик выйдет из зацепления с колесом, а рычаг 15, нажав на кнопочный контакт, выключит двигатель. В комплекте установки имеются грузы 3 и противовесы, хранящиеся в выдвижном ящике 12. Грузы укрепляются в дуговых прорезях дисков. Дуговые прорези выполнены по двум радиусам. Для установки грузов по углу все диски имеют шкалы в градусах с согласованным между собой нулевым отсчетом. Подключение установки электрического питания осуществляется шнуром со штепсельной вилкой и тумблером 14.
Основные параметры установки
1. Питание двигателя от сети переменного тока с напряжением 127 или 220 в.
Примечание. Установка с мотором на 127 в включается в сеть через трансформатор.
2. Потребляемая мощность 40 Вт.
3. Расстояние между соседними дисками 80 мм.
4. Вес: а) грузов —40 г, 50 г, 50 г;
б) противовесов — 60 г, 70 г.
5. Габариты установки 530 X 360 X 355 мм,
6. Общий вес установки 25 кг.
Порядок проведения работы
Принадлежности: установка ТММ-35 с набором грузов, линейка, калькулятор.
1. Составляется форма отчета по лабораторной работе.
2. Веса грузов Qi, расстояние их до оси вращения ri и до плоскости приведения I (Zi), а также углы поворота дисков записать в таблицу 1 (задаются преподавателем).
3. В прорези дисков 1, 2, 3 установить и закрепить неуравновешенные грузы Q1, Q2, Q3,
4. Убедиться в том, что ротор статически и динамически неуравновешен.
Примечание. Ротор при повороте на любой угол стремится занять
одно и то же положение, соответствующее наинизшему положению его центра тяжести.
5. Подсчитать произведения QIrI и QIrIZI и результаты занести в таблицу 1.
6. Построить векторный многоугольник по уравнению (11) (рис. 5, а). Определить модуль замыкающего вектора QIIrIIl. Замерить по чертежу угол aII. Зная 1 = 320 мм и задавшись QII, определить rII.
7. Построить векторный многоугольник по уравнению (1) (рис. 5, б). Определить модуль замыкающего вектора QIrI замерить по чертежу угол aI. Задавшись QI, определить rI.
8. Противовесы QI, QII на радиусах rI и rII установить в плоскостях приведения I и II. Установить диски I и II на углы aI и aII.
9. Проверить статическую уравновешенность ротора. Ротор при повороте на любой угол должен находиться в безразличном равновесии.
10.Проверить динамическую уравновешенность ротора. Разогнать ротор, нажав на шаровую рукоятку рычага 15. Подпружиненная правая опора не должна совершать колебаний.
11. По формулам (12) — (15) подсчитать значения углов aI и aII и значения произведений QIrI и QIIrII и результаты занести в таблицу 2.
Таблица 1.
| № дисков | Qi | ri | zi | ai | Qiri | Qirizi |
| Параметры Плоскость I Плоскость II |
Таблица 2.
| № дисков | Qiri | Qirizi | Qirisinai | Qiricosai | Qirizisinai | Qirizicosai |
| Параметры Плоскость I Плоскость II |
Таблица 3.
| Параметры | Q | r | a | Qr | |
| Плоскость I Плоскость II | Графически Аналитически |
В отчете следует представить:
1. Теоретическую часть.
2. Краткое описание работы и схему установки с расположением неуравновешенных масс.
3. Таблицу 1 для подсчета величин и положений противовесов графическим методом.
4. Планы центробежных и статических моментов в выбранном масштабе.
5. Таблицу 2 аналитического расчета противовесов.
6. Таблицу 3 сравнения графического и аналитического методов.
7. Выводы по результатам экспериментальной проверки.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В каком случае тело будет уравновешено статически?
2. В каком случае тело будет уравновешено динамически?
3. В каком случае тело будет уравновешено полностью?
4. Когда можно «ограничиться статической балансировкой?
5. При каких условиях необходима динамическая балансировка и почему?
6. Как на приборе проверить статическую и динамическую уравновешенность?
7. Что такое «плоскости исправления», как они выбираются?
8. Относительно чего можно взять центробежный момент инерции?
9. Что значит «безразличное равновесие?
10. Что является мерой статической и динамической уравновешенности?
11. Каким образом 2 противовеса в одной плоскости свести к одному противовесу?
12. С какой целью производят уравновешивание вращающихся деталей?
ЛИТЕРАТУРА
1. Артоболевский И.И. Теория механизмов и машин: учебник для вузов.- 5-е изд., стер.- М.: Альянс, 2008.- 640 с.
2. Фролов К.В., Попов С.А., Мусатов А.К. Теория механизмов и механика машин. Учебник для втузов 5-е изд., стер. под ред. Фролова К.В. - Москва: Высшая школа, 2005. - 496 с.
ЛАБОРАТОРНАЯ РАБОТА №4
