Структурный анализ плоских механизмов
КАФЕДРА «МЕХАНИКА»
В.Ф. Белуха, А.В. Саразов, К.В. Худяков
Лабораторный практикум по теории механизмов и машин
для студентов всех форм обучения
Волжский 2012
УДК 531.8
Рецензент:
канд. техн. наук, доцент кафедры ВТО Волжского политехнического института (филиала) ВолгГТУ А.В. Авилов
Издается по решению редакционно-издательского совета
Волгоградского государственного технического университета
В.Ф. Белуха, А.В. Саразов, К.В. Худяков: Лабораторный практикум по теории механизмов и машин. [Электронный ресурс]: методические указания / В.Ф. Белуха, А.В. Саразов, К.В. Худяков //Сборник «Методические указания для выполнения курсового проекта (работы) для студентов дневной, вечерней и заочной форм обучения по курсу «Теория механизмов и машин»».Электрон. текстовые дан.(1файл:4779Kb)-Волгоград: ВПИ (филиал) ВолгГТУ,2012.-систем.требования:Windows 95 и выше; ПК с процессором 486+; CD-ROM.
Содержит указания к выполнению курсового проекта (курсовой работы) по теории механизмов и машин. Задания также могут быть использованы студентами для самоподготовки.
Предназначены для студентов бакалавриата, обучающихся по направлениям: 552100 "Эксплуатация транспортных средств", 200500 «Метрология, стандартизация и сертификация», направлению 552900 « Технология, оборудование и автоматизация машиностроительных производств», специальностям: 210200 «Автоматизация технологических процессов и производств», 170500 «Машины и аппараты химических производств и предприятий строительных материалов». CD-ROM
ÓВолгоградский
государственный технический
университет, 2012 Ó Волжский
политехнический институт, 2012
Содержание
1. Введение…………………………………………………………….4.
2. Лабораторная работа №1…………………………………………..5.
3. Лабораторная работа №2…………………………………………..12.
4. Лабораторная работа №3…………………………………………..19.
5. Лабораторная работа №4…………………………………………..28.
6. Лабораторная работа №5…………………………………………..40.
Введение
Методические указания «Лабораторный практикум по теории механизмов и машин» составлены в соответствие с ФГОС и рабочей программой по ТММ для студентов дневной, вечерней и заочной форм обучения.
В основу указаний положено учебное пособие «Лабораторный практикум по теории механизмов и машин» под редакцией Ю.П. Кислова.
Цель методических указаний помочь студентам в самостоятельной подготовке к лабораторным работам по курсу ТММ.
В методических указаниях по каждой лабораторной работе представлена необходимая краткая теоретическая часть, контрольные вопросы и список литературы.
Лабораторная работа №1:
Структурный анализ плоских механизмов
Цель работы
1. Изучить теорию образования кинематических пар, кинематических целей и механизмов.
2. Разделить заданные схемы механизмов на структурные группы и определить их класс и порядок.
3. Определить класс и порядок заданных механизмов.
Теоретическая часть
При исследовании механизмов необходимо знать, к какому классу они относятся, так как каждому классу соответствует вполне определенный метод кинематического и кинетостатического исследования.
Механизм, построенный правильно с точки зрения структуры, не может вызвать сомнений в смысле однозначности перемещений отдельных звеньев при наличии одного или нескольких начальных звеньев.
К заданному начальному звену (звеньям) и, следовательно, обладающему одной (несколькими) степенью свободы, можно присоединить без изменения общего числа степеней свободы системы такие группы, которые называются структурными группами или группами Ассура.
Предполагаем, что звенья, образующие структурную группу, присоединяются к другим звеньям механизма при помощи кинематических пар пятого класса (низших пар), тогда между числом пар и количеством звеньев, образующих эту группу, должно существовать соотношение:
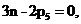
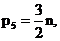
т. е. число звеньев группы n должно быть всегда четным, так как число кинематических пар 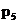 может быть только целым.
может быть только целым.
Наименьшее число звеньев структурной группы равно двум. Такая группа, имеющая два звена и три кинематические пары, называется двухповодковой (рис. 1.1). Здесь пары А и С — условные — «потенциальные», появляющиеся после присоединения группы к какой-либо системе.
Присоединяя группу к одному, двум начальным звеньям, можно получить механизм с одной или с двумя степенями подвижности (рис. 1.2).
Для некоторого n и соответствующего ему 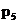 можно построить несколько элементарных групп, не подлежащих разделению. Эти группы целесообразно классифицировать так, чтобы каждому классу соответствовал определенный метод исследования.
можно построить несколько элементарных групп, не подлежащих разделению. Эти группы целесообразно классифицировать так, чтобы каждому классу соответствовал определенный метод исследования.
Л. В. Асур предложил отнести первому классу все элементарные группы, представляющие собой незамкнутую цепочку центральных звеньев с присоединенными к ним свободными поводками.
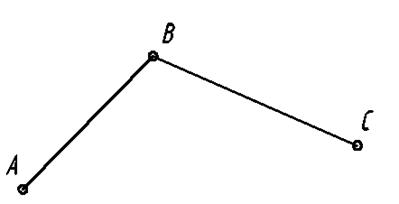
Рис. 1.1
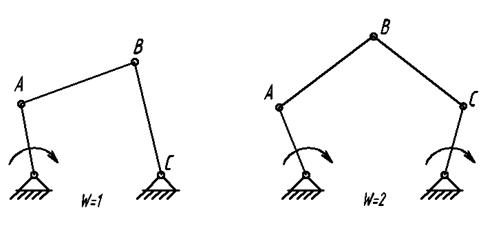
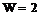
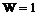
Рис. 1.2
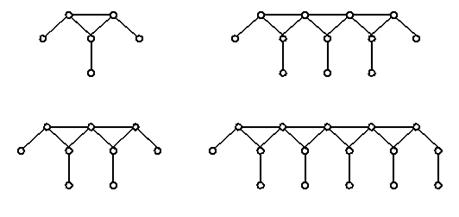
Рис. 1.3
Поводком группы называют звено с двумя элементами кинематических пар, имеющее один свободный элемент для присоединения к механизму. Поводки внешними кинематическими парами могут присоединяться либо к звеньям механизма, либо к неподвижному звену.
Более сложные группы образуются из простейших путем развития поводка.
Порядок группы определяется количеством поводков. Для группы первого класса отличительным признаком является наличие у центральных звеньев хотя бы одного поводка (рис. 1.3).
Если у некоторых центральных звеньев не имеется свободных поводков, то такие группы относятся ко второму классу (рис. 1.4, а). Группы, образующие замкнутый контур, относятся к третьему классу (рис. 1.4, б).
а) б)
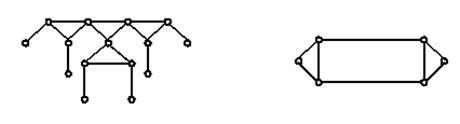
Рис. 1.4
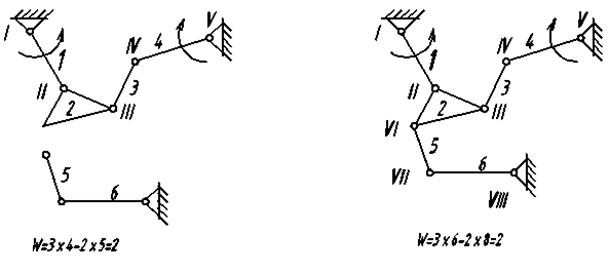
W=3·4-2·5=2 W=3·6-2·8=2
(до присоединения группы) (после присоединения группы 5-6)
Рис. 1.5
При отсутствии поводков группа имеет нулевой порядок (рис. 1.4, б).
Если каждую из перечисленных групп присоединить к неподвижному звену и начальным звеньям или к каким-либо другим звеньям механизма, то данная группа приобретает подвижность. При этом число степеней свободы системы, к которой группа присоединяется, не изменяется (рис. 1.5).
Движение звеньев присоединенной группы будет зависеть от закона движения начального звена.
Число степеней свободы не изменится, если от механизма отнять одну из присоединенных групп. Оставшаяся система будет представлять собой более простой механизм. Этим можно воспользоваться для установления правильности структур механизма, определяющей возможность вынужденного перемещения отдельных звеньев в зависимости от перемещения начального звена, и установить класс и порядок механизма, а также метод, при помощи которого должно проводиться исследование рассматриваемого механизма.
Класс и порядок механизма определяются классом и порядком сложной группы.
Данная классификация структурных групп W=0 является классификацией Ассура.
Академик И. И. Артоболевский предложил свое разделение групп на классы (классификация Артоболевского).
В связи с тем, что различные литературные источники рассматривают и ту и другую классификацию, ниже приводится сравнительная таблица классификации структурных групп по Ассуру и по Артоболевскому (таблица 1.1).
При исследовании структуры механизма (структурном анализе) необходимо учитывать следующее:
1. Наличие лишних степеней свободы и пассивных условий связи. В механизмах, кроме степеней свободы и связей, воздействующих на характер движения механизма, могут встретиться степени свободы и условия связи, не оказывающие никакого влияния на характер движения механизма в целом. целом. Удаление из механизма звеньев и кинематических пар, которые создают эти степени свободы и связи, не меняет общего характера движения механизма. Такие степени свободы называются лишними степенями свободы, а связи — пассивными.
Таблица 1.1
| Группа | По классификации | |
| Ассура Л. В. | Артоболевского И. И. | |
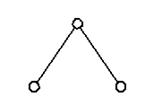 | I класс | II класс |
| 2 порядок | ||
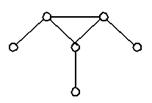 | I класс | III класс |
| 3 порядок | ||
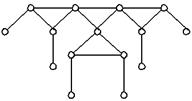 | II класс | III класс |
| 6 порядок | ||
 | III класс | IV класс |
| 0 порядок | 2 порядок | |
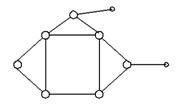 | III класс | IV класс |
| 2 порядок | 3 порядок |
a) W=0 б) W=1
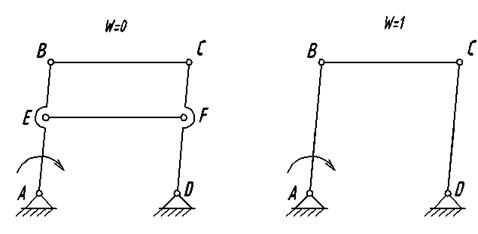
Рис. 1.6
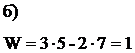
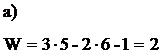
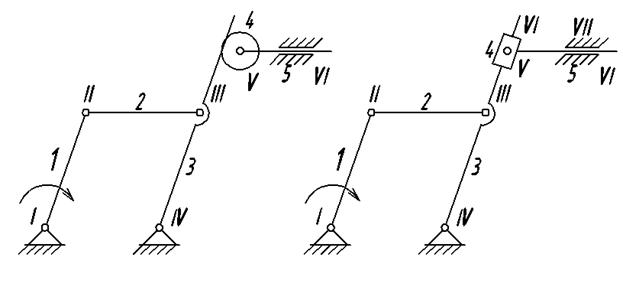
Рис. 1.7
На рис. 1.6, а в механизме (фигура АВСД — параллелограмм) расстояние между точками F и Е остается постоянным и равным расстоянию между точками А и Д, В и С. Без всякого нарушения характера движения механизма звено РЕ можно удалить (рис.1.6,б). Удаленное звено на механизм налагало пассивные связи.
На рис. 1.7а представлен механизм с роликом. Лишняя степень свободы (W=2) объясняется наличием в механизме вращающегося круглого ролика, так как вращение ролика вокруг оси не оказывает никакого влияния на характер движения механизма. Следовательно, ролик можно удалить и механизм представить в следующем виде (рис. 1.7, б).
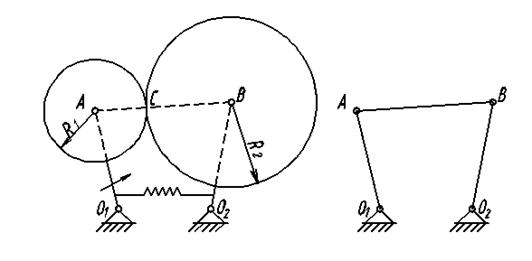
Рис. 1.8
2. Наличие в механизмах сложных шарниров.
Когда в одном шарнире сходятся несколько звеньев (сложный шарнир), число кинематических пар равно числу звеньев без единицы.
3. Высшие пары заменяются низшими по следующему правилу:
а) «разрушают» высшую пару (рис. 1.8);
б) вводят «фиктивное» звено с двумя вращательными кинематическими парами с осями, расположенными в центрах кривизны звеньев, образующих высшую пару;
в) введенное звено соединяют со звеньями, которые входили в высшую пару.
Полученный в результате такой замены механизм называется «заменяющим».
Порядок выполнения работы
Принадлежности: журнал механизмов, бланк отчета, карандаш, линейка.
1. По таблице в журнале механизмов студент выбирает по номеру, полученному от преподавателя, соответствующую задачу (в каждой задаче два механизма).
2. Изобразить кинематические схемы механизмов.
3. Подсчитать число подвижных звеньев механизма.
4. Определить число низших ( 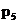 ) и высших кинематических пар (
) и высших кинематических пар ( 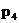 ), входящих в состав механизма.
), входящих в состав механизма.
5. По формуле Чебышева ( 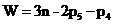 ) определить число степеней свободы механизма, а следовательно, и число начальных (ведущих) звеньев механизма.
) определить число степеней свободы механизма, а следовательно, и число начальных (ведущих) звеньев механизма.
6. Поступательные пары заменить вращательными, имея в виду, что поступательное движение можно рассматривать как вращательное вокруг бесконечно удаленного центра.
7. При наличии высших пар в механизме произвести их замену низшими и построить заменяющий механизм.
8. Построить структурную схему. Структурная схема строится без соблюдения размеров звеньев. Структурная схема включает звенья, соединяющиеся только вращательными парами. Кроме того, всякое звено, имеющее более двух шарниров, даже лежащих на одной прямой, целесообразно изображать в виде многоугольника с числом вершин, равным числу шарниров.
9. Структурную схему разделить на группы, начиная с наиболее удаленной от ведущего звена, пока не останется ведущее звено со стойкой.
10. Определить класс и порядок каждой группы Ассура.
11. Определить класс и порядок всего механизма по наиболее сложной группе.
В отчёт следует представить:
1. Кинематические схемы заданных механизмов, их заменяющие и структурные схемы.
2. Выводы о классе и порядке механизмов, разделенных на структурные группы.
Контрольные вопросы
1. Что называется кинематической парой?
2. Как классифицируются кинематические пары?
3. Что называется кинематической цепью?
4. Какие механизмы относятся к третьему семейству?
5. В чем состоит принцип образования механизмов по Ассуру?
6. Что называется механизмом?
7. Как заменить высшую пару низшей?
8. Как определить число низших пар в сложном шарнире?
9. Как заменить поступательную пару вращательной?
10. Чем определяется число начальных звеньев механизма?
11. Что такое «заменяющий механизм»?
12. Чем структурная схема отличается от кинематической?
13. Каким условиям должна удовлетворять группа Ассура?
14. Что такое «пассивное» звено?
15. Что такое «базисное» звено?
16. Как образуется более сложная группа Ассура?
17. Какие отличительные признаки групп I, II и III классов по классификации Ассура?
18. Как определить класс и порядок групп по классификации Артоболевского?
19. Как определить порядок групп Ассура?
20. Какой порядок разложения механизма на структурные группы?
21. Как определяются класс и порядок всего механизма?
22. Для какой цели проводится структурный анализ механизма?
Литература
1. Артоболевский И.И. Теория механизмов и машин: учебник для вузов.- 5-е изд., стер.- М.: Альянс, 2008.- 640 с.
2. Фролов К.В., Попов С.А., Мусатов А.К. Теория механизмов и механика машин. Учебник для втузов 5-е изд., стер. под ред. Фролова К.В. - Москва: Высшая школа, 2005. - 496 с.
ЛАБОРАТОРНАЯ РАБОТА № 2
Полное уравновешивание (балансировка) вращающихся масс ротора при неизвестном расположении неуравновешенных масс.
Цель работы
1. Определение величины и расположения противовесов в двух произвольно выбранных плоскостях, перпендикулярных оси вращения ротора.
2. Экспериментальная проверка уравновешенности вращающегося ротора.
Порядок проведения работы
Принадлежности: станок типа ТММ-1, набор грузов, калькулятор, бланк-форма отчета по лабораторной работе.
Основные параметры станка ТММ-1:
Собственная частота колебаний рамы — 6—7 герц
Точность измерения амплитуды — 0,01 мм
Цена деления лимба — 1°
Цена деления шкалы дисков — 1 мм
. Вес добавочных грузов — 10, 20, 30, 40 г
Электродвигатель мощностью — 30 Вт
Напряжение питания - 220 В
Вес станка — 56 кг
1. Станок подготавливается к работе:
а) диск 3 по шкале 7 устанавливается на ноль;
б) указатель точного отсчета индикатора 2 устанавливается на ноль;
в) рама 10 по уровню 21 винтами 19 устанавливается в горизонтальное положение.
2. Производится измерение амплитуды А1 при резонансе от собственной неуравновешенности ротора. Амплитуда измеряется три раза и вычисляется ее среднее значение:
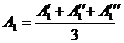
Результаты заносятся в таблицу 1.
Примечание. Во время пуска не следует сильно нажимать на рукоятку 14, т.к. это может повлиять на точность замеряемой амплитуды. Поэтому каждый раз после разгона ротора за резонансное число оборотов нужно осторожным нажатием шток индикатора/ довести до контакта с кронштейном рамы.
3. Преподавателем задается вес добавочного груза Q3 и радиус установки гд. Вычисляется произведение Qд • rд. Добавочный груз QД закрепляется в прорези диска 3 на выбранном расстоянии rд. Три раза измеряется при резонансе амплитуда А2 колебаний рамы и вычисляется ее среднее значение:
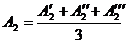
Результаты заносятся в таблицу 2.
4. Освобождаются винты 5, диск 3 поворачивается на валу ротора на 180° и закрепляется. Снова измеряется три раза при резонансе амплитуда A3 и вычисляется ее среднее значение:
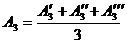
Результаты заносятся в таблицу 2.
5. По таблицам 5 бланка производится вычисление радиуса противовеса гп и угла aп между нулевым диаметром и направлением радиуса-вектора гп (Qn — нужно задаться).
6. Рассчитанный противовес устанавливается в плоскости I-I (добавочный груз снимается) и производится контрольная балансировка. Она делается при четырех углах: +a; —a; 180° +a; 180°—a (так как при начальной установке добавочного груза не фиксируется его положение относительно нуля).
Окончательным углом установки противовеса считается тот, при котором остаточная амплитуда Ак имеет минимальную величину. Она измеряется три раза, и определяется ее среднее значение
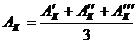
Затем определяют относительную величину остаточной неуравновешенности
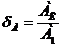
Результаты заносятся в таблицу 3.
7. Уравновешивание в плоскости II—II проводится аналогично. Для этого необходимо плоскости I—I и II—II поменять местами, т. е. ротор раскрепляется в подшипниках.
В отчете следует представить:
1. Теоретическую часть.
2. Схему баланбировочного станка с балансируемым ротором.
3. Таблицу 1 для определения максимальной амплитуды колебаний при резонансе от собственной неуравновешенности ротора (A1) и добавочными грузами (А2 и А3).
4. Таблицу 2 вычисления веса первого противовеса QI и его положение (rI и aI).
5. Таблицу 3 контрольной балансировки.
6. Таблицы 1, 2, 3 с вычислениями веса второго противовеса QПII и его положение (rПII и aПII).
7. Выводы.
Таблица 1.
| Амплитуда | Измерения | Вес и радиус положения добавочного груза | |||
| №1 | №2 | №3 | Среднее | ||
| А1 А2 А3 |
Таблица 2.
| № п/п | Вычисляемые величины и формулы для вычислений | Результат |
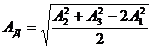 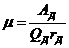 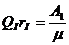 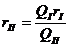 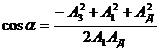 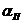 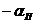 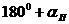 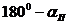 |
Таблица 3
| Амплитуда | Измерения | 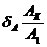 | |||
| №1 | №2 | №3 | Среднее | ||
| А(a) A(-a) A(a+180°) A(-a-180°) |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В каких случаях для балансировки роторов применяются специальные балансировочные станки (машины)?
2. При каком условии наступает явление резонанса?
3. На чем основан принцип определения величины и положения неуравновешенных масс в станке Б. В. Шитикова?
4. Почему проверка сбалансированности ротора проводится при 4 углах?
5. Условие полного уравновешивания вращающегося ротора?
6. В чем недостаток станка Б. В. Шитикова?.
ЛИТЕРАТУРА
1. Артоболевский И.И. Теория механизмов и машин: учебник для вузов.- 5-е изд., стер.- М.: Альянс, 2008.- 640 с.
2. Фролов К.В., Попов С.А., Мусатов А.К. Теория механизмов и механика машин. Учебник для втузов 5-е изд., стер. под ред. Фролова К.В. - Москва: Высшая школа, 2005. - 496 с.
ЛАБОРАТОРНАЯ РАБОТА № 3
Цель работы
Целью работы является графическое и аналитическое определение величин и расположения противовесов при статическом и динамическом уравновешивании трех известных точечных масс, а также экспериментальная проверка выполненных расчетов.
Пусть имеется ротор (рис. 4), в плоскостях которого 1,2 и 3, перпендикулярных оси вращения, имеются неуравновешенные массы mi, m2. m3. Положения неуравновешенных масс в плоскостях заданы радиус-векторами г1 г2, г3. Положение плоскостей 1, 2 и 3 относительно плоскости приведения X определяется соответственно координатами z1, z2 и z3. Противовесы устанавливаются в плоскости I и плоскости II, расстояние между ними l. Обозначим вес противовеса при статическом уравновешивании через Qп, а радиус-вектор, определяющий положение его центра тяжести, через rп, Тогда условием уравновешенности ротора (здесь массы заменяют их весами) будет:
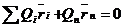 (9)
(9)
При полном уравновешивании ротора веса противовесов устанавливаемых в плоскости I и II, обозначим QI и QII, a радиус-векторы, определяющие положения их центров тяжести, через rI и rII. Тогда условиями полного уравновешивания будут:
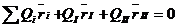 (10)
(10)
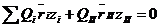 (11)
(11)
При аналитическом решении этой задачи уравнение (9) развернется в два уравнения проекций на оси координат, а уравнение (10) и (11) в четыре уравнения проекций на оси координат.
Совокупность уравнений (10) и (11) является условием полного уравновешенного ротора. Решение этих уравнений сводится к определению весов и положений противовесов и может быть осуществлено аналитически и графически.
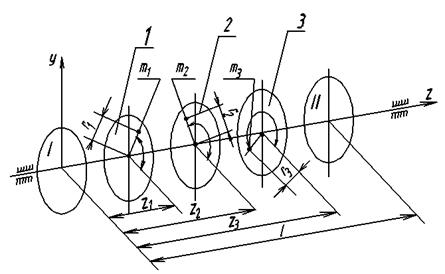
Рис.4
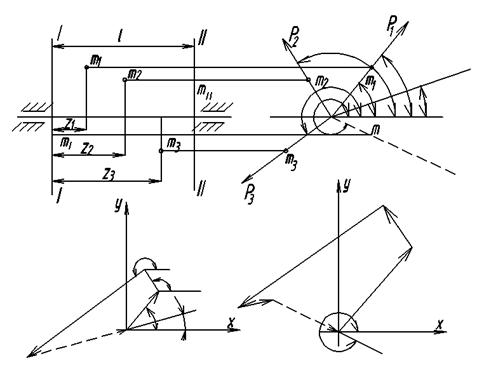
Рис. 5
В обоих случаях сначала решается уравнение (11) и определяются вес и положение противовеса при динамическом уравновешивании. Затем решается уравнение (11).
Более: удобным является графический метод, который заключается в построении векторных многоугольников по уравнениям (10) и (11). Сначала строится векторный многоугольник центробежных моментов инерции по уравнению (11), рис. 5, а. Так как суммарный вектор должен быть равен нулю, то замыкающий вектор многоугольника определяет собой произведение 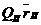 l.
l.
Координата zII известна и равна 1 расстоянию между плоскостями исправления. Из этого произведения можно определить rII, задавшись весом противовеса QII. Угол aII, дающий направление радиуса-вектора противовеса, измеряется по чертежу, затем строится многоугольник по уравнение (10), рис. 5, б. В этом многоугольнике неизвестной величиной будет замыкающий вектор, модуль которого равен QIirI.. Задаваясь QI определяем rI. По чертежу замеряется угол определяющий направление радиуса-вектора противовеса.
Все эти величины, исходя из уравнений (10) и (11), можно вычислить аналитически по соответствующим формулам и сопоставить с результатами графического метода:
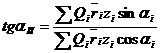 (12)
(12)
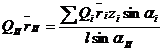 (13)
(13)
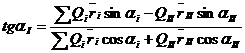 (14)
(14)
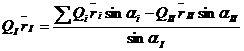 (15)
(15)
Описание установки
| |
| |

| |

| |

| |

| |

| |

| |


| |
| |

| |

| |



Общий вид установки ТММ-35 представлен на рис.. 6.
Рис. 6.
На чугунном основании II закреплены стойки 10 и 18. В стойках закреплены шариковые подшипники вала ротора. На валу ротора установлено пять дисков 2. В крайних дисках (I и II) располагаются противовесы. Три средних диска служат для установки неуравновешенных грузов. Шарикоподшипник правого конца вала I установлен в корпусе 4, который на миниатюрных шарикоподшипниках 6 может перемещаться в горизонтальном направлении по планке 7. Корпус, 4 оттягивается в разные стороны пружинами 8, закрепленными другими концами на кронштейнах 5 при помощи винтов с гайками 9. Если правый конец ротора слегка отвести в сторону и отпустить, то он начнет совершать колебания в горизонтальной плоскости вокруг левой опоры. Разгон ротора осуществляется двигателем 13, закрепленным на рычаге 15. При нажиме вниз на шариковую рукоятку рычага 15, последний, поворачиваясь на оси кронштейна 20, поднимает двигатель 13 вверх и прижимает обрезиненный ролик вала двигателя к фрикционному колесу, закрепленному на валу ротора. Одновременно рычаг 15 освобождает кнопочный контакт, включающий двигатель в работу. Если отпустить шаровую рукоятку рычага 15, то под действием собственного веса двигатель опустится вместе с рычагом 15 вниз, причем ролик выйдет из зацепления с колесом, а рычаг 15, нажав на кнопочный контакт, выключит двигатель. В комплекте установки имеются грузы 3 и противовесы, хранящиеся в выдвижном ящике 12. Грузы укрепляются в дуговых прорезях дисков. Дуговые прорези выполнены по двум радиусам. Для установки грузов по углу все диски имеют шкалы в градусах с согласованным между собой нулевым отсчетом. Подключение установки электрического питания осуществляется шнуром со штепсельной вилкой и тумблером 14.
Основные параметры установки
1. Питание двигателя от сети переменного тока с напряжением 127 или 220 в.
Примечание. Установка с мотором на 127 в включается в сеть через трансформатор.
2. Потребляемая мощность 40 Вт.
3. Расстояние между соседними дисками 80 мм.
4. Вес: а) грузов —40 г, 50 г, 50 г;
б) противовесов — 60 г, 70 г.
5. Габариты установки 530 X 360 X 355 мм,
6. Общий вес установки 25 кг.
Порядок проведения работы
Принадлежности: установка ТММ-35 с набором грузов, линейка, калькулятор.
1. Составляется форма отчета по лабораторной работе.
2. Веса грузов Qi, расстояние их до оси вращения ri и до плоскости приведения I (Zi), а также углы поворота дисков записать в таблицу 1 (задаются преподавателем).
3. В прорези дисков 1, 2, 3 установить и закрепить неуравновешенные грузы Q1, Q2, Q3,
4. Убедиться в том, что ротор статически и динамически неуравновешен.
Примечание. Ротор при повороте на любой угол стремится занять
одно и то же положение, соответствующее наинизшему положению его центра тяжести.
5. Подсчитать произведения QIrI и QIrIZI и результаты занести в таблицу 1.
6. Построить векторный многоугольник по уравнению (11) (рис. 5, а). Определить модуль замыкающего вектора QIIrIIl. Замерить по чертежу угол aII. Зная 1 = 320 мм и задавшись QII, определить rII.
7. Построить векторный многоугольник по уравнению (1) (рис. 5, б). Определить модуль замыкающего вектора QIrI замерить по чертежу угол aI. Задавшись QI, определить rI.
8. Противовесы QI, QII на радиусах rI и rII установить в плоскостях приведения I и II. Установить диски I и II на углы aI и aII.
9. Проверить статическую уравновешенность ротора. Ротор при повороте на любой угол должен находиться в безразличном равновесии.
10.Проверить динамическую уравновешенность ротора. Разогнать ротор, нажав на шаровую рукоятку рычага 15. Подпружиненная правая опора не должна совершать колебаний.
11. По формулам (12) — (15) подсчитать значения углов aI и aII и значения произведений QIrI и QIIrII и результаты занести в таблицу 2.
Таблица 1.
| № дисков | Qi | ri | zi | ai | Qiri | Qirizi |
| Параметры Плоскость I Плоскость II |
Таблица 2.
| № дисков | Qiri | Qirizi | Qirisinai | Qiricosai | Qirizisinai | Qirizicosai |
| Параметры Плоскость I Плоскость II |
Таблица 3.
| Параметры | Q | r | a | Qr | |
| Плоскость I Плоскость II | Графически Аналитически |
В отчете следует представить:
1. Теоретическую часть.
2. Краткое описание работы и схему установки с расположением неуравновешенных масс.
3. Таблицу 1 для подсчета величин и положений противовесов графическим методом.
4. Планы центробежных и статических моментов в выбранном масштабе.
5. Таблицу 2 аналитического расчета противовесов.
6. Таблицу 3 сравнения графического и аналитического методов.
7. Выводы по результатам экспериментальной проверки.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В каком случае тело будет уравновешено статически?
2. В каком случае тело будет уравновешено динамически?
3. В каком случае тело будет уравновешено полностью?
4. Когда можно «ограничиться статической балансировкой?
5. При каких условиях необходима динамическая балансировка и почему?
6. Как на приборе проверить статическую и динамическую уравновешенность?
7. Что такое «плоскости исправления», как они выбираются?
8. Относительно чего можно взять центробежный момент инерции?
9. Что значит «безразличное равновесие?
10. Что является мерой статической и динамической уравновешенности?
11. Каким образом 2 противовеса в одной плоскости свести к одному противовесу?
12. С какой целью производят уравновешивание вращающихся деталей?
ЛИТЕРАТУРА
1. Артоболевский И.И. Теория механизмов и машин: учебник для вузов.- 5-е изд., стер.- М.: Альянс, 2008.- 640 с.
2. Фролов К.В., Попов С.А., Мусатов А.К. Теория механизмов и механика машин. Учебник для втузов 5-е изд., стер. под ред. Фролова К.В. - Москва: Высшая школа, 2005. - 496 с.
ЛАБОРАТОРНАЯ РАБОТА №4
КРАТКАЯ ТЕОРИЯ ВОПРОСА
Нарезание эвольвентных профилей методом обката или огибания является наиболее распространенным способом производства зубчатых колес. Режущим инструментом в этом случае могут быть зубчатая рейка (гребенка), червячная фреза и долбяк в виде шестерни. Нарезание колес производится соответственно на зубострогательном, зуборезном или зубодолбежном станках.
Предположим, что колеса изготавливаются по методу обкатки (огибания) инструментом реечного типа (инструментальной рейкой, червячной фрезой), который профилируется на основе исходного контура (ГОСТ 3058—54).
Приступая к изготовлению колес, образующих зубчатое зацепление, нужно для каждого из них выточить заготовку радиуса Re (радиус окружности выступов), об определении которого будет сказано ниже, а также подсчитать радиус rД делительной окружности и общий для обоих колес шаг p на делительных окружностях по формулам
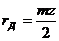 (1)
(1)
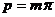 (2)
(2)
Все остальные размеры каждого из колес определяются геометрическими параметрами инструментальной рейки, а также положением ее по отношению к обрабатываемому колесу в процессе его изготовления.
Ознакомимся с размерами инструментальной рейки (рис.1.1), а также с процессом обработки колес по методу обкатки.
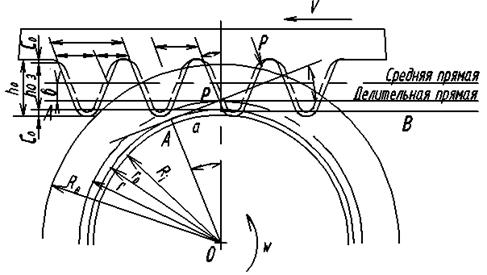
Рис.1.1
Прямая линия, делящая высоту зубьев рейки пополам, называется средней (модульной) прямой. Прямые, параллельные средней прямой, называются делительными. Расстояние между правыми или левыми профилями двух соседних зубьев, измеряемое по любой делительной прямой, называется шагом рейки. Для обработки колеса нужно взять рейку, шаг которой равен шагу p колеса на его делительной окружности, определяемому формулой (2).
Ширина впадины и толщина зуба равны между собой, только на средней прямой. На делительных прямых они не равны, причем, чем ближе делительная прямая к линии выступов, тем ширина впадины больше, а толщина зуба меньше. Ширину впадины обозначим буквой SД. Высота h0 зуба рейки состоит из отрезка h0З и двух равных отрезков С0. Отрезок h0З - глубина захода рейки, С0 - радиальный зазор, a0 - профильный угол рейки. У основания и у вершины зуба имеется закругление радиуса rи. Все размеры рейки зависят от модуля m:
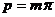 (3)
(3)
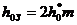 (4)
(4)
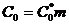 (5)
(5)
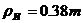 (6)
(6)
где 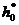 - коэффициент высоты зуба рейки;
- коэффициент высоты зуба рейки;
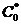 - коэффициент радиального зазора.
- коэффициент радиального зазора.
Для образования угла заострения, необходимого при снятии стружки, боковые грани зубьев скошены (пунктир на рис. 1.1).
Процесс изготовления зубчатого колеса (рис. 1.1) инструментальной рейкой по методу обкатки заключается в том, что рейка в движении по отношению к обрабатываемому колесу перекатывается без скольжения одной из своих делительных прямых или средней прямой по делительной окружности колеса (движение обкатки) и одновременно совершает быстрые возвратно-поступательные перемещения вдоль оси колеса, снимая при этом стружку (рабочее движение).
Для осуществления такого перекатывания нужно рейке сообщить поступательное движение влево со скоростью V, определяемой по формуле
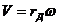 (7)
(7)
где w - угловая скорость колеса.
Расстояние между средней прямой рейки и той делительной прямой, которая в процессе
