Логическое сложение (дизъюнкция).

Сложение

Пример 1. Сложим числа 15 и 6 в различных системах счисления.

Шестнадцатеричная: F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2 . 81 + 5 . 80 = 16 + 5 = 21, 1516 = 1 . 161 + 5 . 160 = 16+5 = 21.

Вычитание

Пример 2 Вычтем единицу из чисел 10₂, 10₈ и 10₁₆



3) Умножение

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Пример 3.

Ответ: 5 ^. 6 = 30₁₀ = 11110₂ = 36₈.
Проверка. Преобразуем полученные произведения к десятичному виду:
11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;
36₈ = 3*8¹ + 6*8⁰ = 30.

Задания для самостоятельной работы

1 вариант

2 вариант

1.Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы: а)10110112; б)0,10001102; в)5178; г)123,418; д)1F16; е)1DE,C816. 2.Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: а)12510; б)206,12510. 3.Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: а)1001111110111,01112; б)10111001,1011001112; в)10111,11111011112. 4.Переведите в двоичную и восьмеричную системы шестнадцатеричные числа: а)2СE16; б)ABCDE16. 5.Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: а)10111012 и 11101112; б)378 и 758; в)A16 и F16; г)A,B16 и E,F16. 6.Вычтите: а)1112 из 101002; б)158 из 208; в)56,78 из 1018; г)1А16 из 3116; д)D,116 из B,9216. 7.Перемножьте числа, а затем проверьте результаты, выполнив соответствующие десятичные умножения: а)1011012 и 1012; б)1011,112 и 101,12. 8.Вычислите значение выражения 2568 + 10110,12 . (608 + 1210) - 1F16. 9.В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание. 10.Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

1.Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы: а)101101112; б)110100,112; в)10108; г)0,348; д)ABC16; е)0,А416. 2.Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: а)22910; б)37,2510. 3.Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы: а)1110101011,10111012; б)1011110011100,112; в)1100010101,110012. 4.Переведите в двоичную и восьмеричную системы шестнадцатеричные числа: а)9F4016; б)1ABC,9D16. 5.Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения: а)1011,1012 и 101,0112; б)1658 и 378; в)1916 и C16; г)E916 и F16. 6.Вычтите: а)10,112 из 100,12; б)478 из 1028; в)16,548 из 30,018; г)F9E16 из 2А3016; д)ABC16 из 567816. 7.Перемножьте числа, а затем проверьте результаты, выполнив соответствующие десятичные умножения: а)1111012 и 11,012; б)1012 и 1111,0012. 8.Вычислите значение выражения 2568 + 10110,12 . (608 + 1210) - 1F16. 9.В системе счисления с некоторым основанием число 12 записывается в виде 110. Укажите это основание. 10.Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

Лабораторная работа №3
«Основы алгебры логики»

Цели работы:

- отработка навыков и умений упрощения сложных логических выражений с помощью законов алгебры логики;

- формирование умений строить таблицы истинности логических выражений;

- формирование умений применять понятийный аппарат алгебры логики для решения логических задач.

Теоретическая часть

Основными логическими операциями являются логическое сложение (дизъюнкция), логическое умножение (конъюнкция), логическое отрицание (инверсия), логическое следование (импликация) и логическое равенство (эквиваленция).

Решение логических задач

Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:

· средствами алгебры логики;

· табличный;

· с помощью рассуждений.

Многоколончатая верстка

1.Для того чтобы текст на странице был размещен в несколько колонок, необходимо в пункте меню «Формат» выбрать команду «Колонки…».

2.В появившемся окне «Колонки» необходимо задать нужное количество колонок, размеры колонок и, если это необходимо, разделитель колонок.

3.Переход на новую колонку происходит автоматически по окончании свободного места в колонке. Если же необходимо перейти на новую колонку ранее, чем закончится колонка, нужно в пункте меню «Вставка» выбрать команду «Разрыв…» и в появившемся окне «Разрыв» установить переключатель на позицию «новую колонку» и нажать кнопку «OK».

4.Если необходимо, чтобы очередной текст располагался в одной колонке, необходимо:

– задать разрыв на новый раздел с нужной страницы;

– задать одну колонку.

5.Для того чтобы уже набранный в одну колонку фрагмент текста был расположен в несколько колонок, необходимо:

– выделить данный фрагмент текста;

– выполнить команды 1-2.

Работа со списками

Все списки можно разделить на 3 вида:

– нумерованные, в которых в качестве обозначения элемента списка служит цифра (римская и арабская) или буква (русская и латинская);

– маркированные, в которых в качестве обозначения элемента списка служит знак (кружок, ромб, черта и др.);

– многоуровневые, в которых в качестве элемента списка может содержаться другой список.

1.Для задания нумерованного списка необходимо в пункте меню «Формат» выбрать команду «Список…».

2.В появившемся окне «Список» на вкладке «Нумерованный» необходимо выбрать нужный список, либо нажать на кнопку «Изменить», задав свой список.

3.Для задания маркированного списка необходимо выполнить команды 1-2, но нужный список выбирать на вкладке «Маркированный».

4.Для задания многоуровневого списка, необходимо выполнить команды 1-2, но нужный список выбирать на вкладке «Многоуровневый».

5.Для задания собственного вида многоуровневого списка, необходимо на вкладке «Многоуровневый» нажать на кнопку «Изменить». В появившемся окне «Изменение многоуровневого списка» необходимо поочередно для каждого уровня задать формат номера и интервал.

6.При работе с многоуровневым списком, для перехода на следующий уровень необходимо нажать на клавиатуре клавишу <Tab>. Для перехода на предыдущий уровень необходимо одновременно нажать клавиши <Shift> и <Tab>.

Работа с таблицами в текстовом редакторе

Рисование таблицы

1.Для того чтобы самостоятельно создать структуру таблицы (нарисовать ее строки и столбцы), необходимо вывести на экран панель инструментов «Таблицы и границы», выбрав в пункте меню «Таблица» команду «Нарисовать таблицу».

2.На появившейся панели инструментов «Таблицы и границы» необходимо нажать на кнопку .

3.Выбирая тип линии и ее толщину, необходимо начертить строки и столбцы таблицы.

4.Инструмент «Ластик» позволяет удалить лишние и ненужные линии.

Работа со строками и столбцами

1.Для того чтобы сделать одинаковую ширину столбцов или высоту строк, необходимо в пункте меню «Таблица» выбрать команду «Автоподбор» и выбрать необходимую команду.

2.Для удаления таблицы, строк, столбцов и ячеек необходимо в пункте меню «Таблица» выбрать команду «Удалить» и нажать левой клавишей мыши на нужную опцию.

3.Для выделения таблицы, строки, столбца или ячейки необходимо в пункте меню «Таблица» выбрать команду «Выделить» и нажать левой клавишей мыши на нужную опцию.

Работа с табличным текстом

1.Для задания направления текста в ячейке (горизонтальное, вертикальное), необходимо нажать правой клавишей мыши в нужной ячейке и в появившемся контекстном меню выбрать команду «Направление текста…».

2.Для выбора способа выравнивания текста в ячейке таблицы, необходимо нажать правой клавишей мыши в ячейке и в появившемся контекстном меню выбрать команду «Выравнивание в ячейке», установить один из девяти способов выравнивания.

3.Для установки заливки в ячейке, необходимо нажать правой клавишей мыши в ячейке и в появившемся контекстном меню выбрать команду «Свойства таблицы…», далее нажать на командную кнопку «Границы и заливка…», активировать вкладку «Заливка» и в появившемся диалоговом окне «Заливка» установить необходимые параметры заливки:

– цвет заливки;

– узор заливки;

– к чему применяется заливка (абзацу, ячейке, таблице).

Адресация ячеек таблицы

Все строки и столбцы таблицы имеют свою нумерацию. Строки таблицы нумеруются арабскими цифрами 1, 2, 3, …Столбцы таблицы нумеруются латинскими буквами или их сочетаниями a, b, c, …, aa, ab, … Для обращения к ячейке необходимо указать номер столбца и номер строки, на пересечении которых она находится: a1, b2, c12, …

Если группа ячеек таблицы образует прямоугольную область, то такая группа называется диапазоном ячеек. Для обращения к диапазону ячеек указывают адрес левой верхней ячейки диапазона и через двоеточие адрес правой нижней ячейки. Если диапазон образуют ячейки только одного столбца, то вместо адреса левой верхней ячейки просто указывается адрес верхней ячейки. Например, a1:b3, b8:c:10, a1:a10.

Вычисления в ячейках таблицы

MicrosoftWordпозволяет выполнять несложные вычисления в ячейках таблицы. Например, такие действия, как подсчет суммы значений ячеек, количества ячеек в диапазоне, среднего значения ячеек и пр. под силу данному текстовому процессору.

Для того чтобы Wordмог произвести вычисления в ячейке таблицы, необходимо вставить формулу:

1.Разместить текстовый курсор в той ячейке, в которой будет происходить вычисление.

2.В пункте меню «Таблица» выбрать команду «Формула…».

3.В появившемся диалоговом окне «Формула» указать необходимые параметры:

– ввести формулу, которая должна начинаться со знака «=»и может включать в себя адреса ячеек, диапазоны ячеек, числа, функции, знаки арифметических операций (+, -, *, /). Например:

=a1/a2+(c5-a2*b2)

– если необходимо, указать формат вывода числа (количество знаков в дробной части, проценты, рубли и пр.).

Функции:

а) ABS(адрес ячейки) – возвращает модуль значения ячейки с указанным адресом;

б) COUNT(диапазон ячеек) – вычисляет количество ячеек в диапазоне. Например: count(b1:c12);

в) MAX(диапазон ячеек или их адреса через «;») – максимальное значение диапазона ячеек. Например, MAX(a1:b12; c13; d14);

г) MIN(диапазон ячеек или их адреса через «;») - минимальное значение диапазона ячеек. Например, MIN(a1:b12; c13; d14);

д) SUM(диапазон ячеек или их адреса через «;») – сумма значений ячеек из диапазона. Например, SUM(a1:b12; c13; d14);

е) AVERAGE(диапазон ячеек или их адреса через «;») – среднее арифметическое значений ячеек из диапазона. Например, AVERAGE(a1:b12; c13; d14).

Построение диаграмм по табличным данным

1) Для построения диаграммы необходимо выделить те ячейки, по значениям которых будет строиться диаграмма.

2) В пункте меню «Вставка» выбрать команду «Рисунок - Диаграмма».

3) Если необходимо, то изменить данные в появившейся таблице:

4) Щелкнуть левой клавишей мыши в любом свободном месте рабочего поля окна текстового процессора. На листе появится диаграмма:

Правила записи формул

1. Запись формулы начинается со знака равенства «=».

2. Формула может содержать адреса ячеек, знаки арифметических операций (+, -, *, /), знаки операций сравнения (>, <, =, >= - больше или равно, <= - меньше или равно, <> - не равно), числовые константы, встроенные функции, круглые скобки.

3. Арифметические операции выполняются согласно их приоритету, если не указан скобками порядок их выполнения.

4. В записи формулы зависящие ячейки выделяются цветом.

5. При вводе формулы в ячейку таблицы активизируется режим отображения формулы. Для перехода в режим отображения значения формулы необходимо нажать на клавишу <Enter> на клавиатуре.

Например, для вычисления в ячейке B6 среднего арифметического данных, содержащихся в ячейках B2, B3 и B4 потребуется формула =(B2+B3+B4)/3.

При выполнении расчетов существует возможность обращения не только к отдельной ячейке, но и к их группе, представляющей прямоугольную область. Такая группа ячеек называется диапазоном ячеек. Для обращения к диапазону ячеек необходимо указать адрес его левой верхней ячейки и через двоеточие адрес правой нижней ячейки. Например: A1:B4, АА3:BX5, G4:G19.

Относительная адресация

Пусть необходимо с использованием Microsoft Excel разработать таблицу, которая бы по введенной цене билета на некоторый автобусный рейс и количеству билетов, определяла бы стоимость. Пусть в ячейках A2:A5 будут содержаться данные о стоимости билетов, в ячейках B2:B5 – данные о количестве, в ячейках C2:C5 должны содержаться формулы для подсчета стоимости, зависящие от A2:A5 и B2:B5. В ячейке C2 будет формула =A2*B2, в ячейке C3 будет формула =A3*B3, в ячейке C4 будет формула =A4*B4, в ячейке C5 будет формула =A5*B5.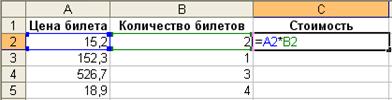

Можно увидеть, что формулы в ячейках C2:C5 будут однотипные, меняются в них только адреса строк. В Microsoft Excel нет необходимости вводить несколько раз однотипные формулы, их можно скопировать. Причем, по принципу относительной адресации при копировании формул по строкам, в них меняются номера строк (увеличиваются или уменьшаются), а при копировании формулы по столбцам – меняются номера столбцов. Для копирования формулы одного и того же диапазона необходимо нажать левой кнопкой мыши на правый нижний угол табличного курсора (черный прямоугольник в ячейке) и, не отпуская клавиши мыши, вести до последней ячейки диапазона.

Абсолютная адресация

Изменим предыдущую задачу следующим образом: пусть к любой стоимости каждого билета будет добавлен комиссионный сбор. Тогда формула для подсчета итоговой стоимости будет иная. Разместим в ячейке D2 значение комиссионного сбора.

Тогда формула в ячейке C2 будет такая: (A2+D2)*B2. Скопировав формулу в ячейки C3:C5 по принципу относительной адресации мы получим формулы: (A3+D3)*B3, (A4+D4)*B4, (A5+D5)*B5, но такие формулы нам не дадут верные результаты, ведь значение комиссионного сбора располагается только в одной ячейке.

Принцип абсолютной адресации дает возможность не менять в формуле при копировании некоторую ячейку или часть ее адреса. Для этого в формуле к обеим частям адреса или к отдельной ее части добавляют знак «$». Например, запись $A$10 означает, что при копировании в формуле всегда будет адрес ячейки A10, запись $A10 означает, что при копировании не будет меняться только адрес столбца, запись A$10 означает, что при копировании не будет меняться только адрес строки.

Таким образом, формула в ячейке C2 должна быть такая: (A2+$D$2)*B2. Ее можно копировать в ячейки C3:C5, при этом адрес ячейки D2 не будет меняться при копировании формулы.

Задания для самостоятельной работы

1.Запустить табличный процессор Microsoft Excel.

2.Задать имя первого листа «Анализ КР».

3.На листе «Анализ КР» создать таблицу «Анализ контрольной работы по математике» следующего вида:

Анализ контрольной работы по математике
Школа:	№5
Класс:	3 «А», 3 «Б», 3 «В»
Учитель:
Дата проведения урока:
Число учащихся по списку
Учащихся, выполнявших работу	Человек	%
Учащихся, справившихся с работой	Человек	%
Получили отметки
Отметка	Человек	%
5
4
3
2
Учитель: __________________( )

4.В ячейке для ввода фамилии и имени учителя ввести свои данные.

5.В ячейке для ввода даты проведения урока ввести текущую дату.

6.В ячейке для ввода числа учащихся по списку ввести произвольное целочисленное значение.

7.В ячейке для ввода числа учащихся, выполнявших работу, ввести значение, не превышающее числа учащихся по списку.

8.В ячейке для ввода числа учащихся, справившихся с работой, ввести значение, не превышающее числа учащихся, выполнявших работу.

9.В ячейках для ввода отметок ввести значения, в совокупности, не превышающие числа учащихся, выполнявших работу.

10.В ячейках для ввода процентов ввести формулы для подсчета процентных отношений числа человек, выполнявших работу, справившихся с работой и их отметок.

11.В последней ячейке в скобках указать свою фамилию и инициалы.

12.Активировать второй лист и задать ему имя «Доход населения».

13.В текущем листе создать таблицу «Среднемесячный доход жителей поселка Новый нетрудоспособного возраста» следующего вида:

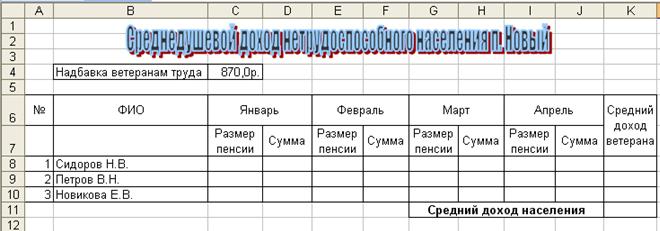
14.В соответствующие ячейки ввести значения фамилий 15 пенсионеров и размеров их пенсий за январь, февраль, март и апрель произвольным образом.

15.Там, где это необходимо, задать денежный формат ячеек.

16.В ячейках «Сумма» ввести формулу для подсчета суммы пенсии за каждый месяц с учетом постоянной надбавки ветеранам труда.

17.В ячейках «Средний доход ветерана» ввести формулы для подсчета средней суммы пенсии каждого ветерана за 4 месяца.

18.В ячейке «Средний доход населения» ввести значение среднего дохода всех ветеранов.

19.Сохранить рабочую книгу под именем Лабораторная работа №7_Фамилия.xls, указав в имени файла свою фамилию.

Лабораторная работа №8
«Использование электронных таблиц для решения математических задач»

Цели работы:

- отработка навыков и умений внедрения в формулы различных математических функций, используя мастер функций;

- отработка навыков использования математических функций на примере решения математических задач.

Теоретическая часть

Мастер функций

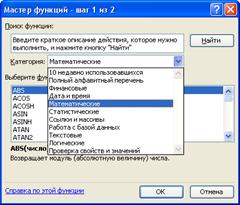В Microsoft Excel для проведения различного рода вычислений содержаться встроенные функции, внедрение которых в ячейку или в формулу в ячейке возможна с помощью мастера функций. Для его запуска необходимо в пункте меню «Вставка» выбрать команду «Функция». В появившемся диалоговом окне «Мастер функций – шаг 1 из 2» нужно выбрать из списка категорию функций, затем дважды щелкнуть по имени нужной функции.

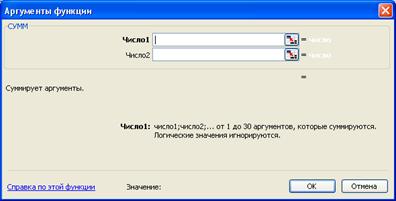В появившемся окне «Аргументы функции» ввести с клавиатуры адрес ячейки или нажать на кнопку перед знаком «=» и щелкнуть мышью на нужную ячейку.

Математические функции в Excel

ABS

Возвращает модуль (абсолютную величину) числа. Абсолютная величина числа - это число без знака.

ABS(число)

Число — это действительное число, модуль которого требуется найти.

COS

Возвращает косинус заданного угла.

COS(число)

Число — это угол в радианах, для которого определяется косинус.

Если угол задан в градусах, умножьте его на ПИ()/180 или используйте функцию РАДИАНЫ, чтобы преобразовать его в радианы.

КОРЕНЬ

Возвращает положительное значение квадратного корня.

КОРЕНЬ(число)

Число — число, для которого вычисляется квадратный корень.

СТЕПЕНЬ

Возвращает результат возведения числа в степень.

СТЕПЕНЬ(число;степень)

Число — основание. Оно может быть любым вещественным числом.

Степень — показатель степени, в которую возводится основание.

Вместо функции СТЕПЕНЬ для возведения в степень можно использовать оператор ^, например 5^2.

EXP

Возвращает число «e», возведенное в указанную степень. Число «e» равно 2,71828182845904 и является основанием натурального логарифма.

EXP(число)

Число — это число, для которого вычисляется экспоненциальная функция с основанием «e».

TAN

Возвращает тангенс заданного угла.

TAN(число)

Число — угол в радианах, для которого определяется тангенс.

Математические функции

СУММ

Суммирует все числа в интервале ячеек.

СУММ(число1;число2; ...)

Число1, число2,... — от 1 до 30 аргументов, для которых требуется определить итог или сумму.

СУММЕСЛИ

Суммирует ячейки, заданные критерием.

СУММЕСЛИ(диапазон;критерий;диапазон_суммирования)

Диапазон — диапазон вычисляемых ячеек.

Критерий — критерий в форме числа, выражения или текста, определяющего суммируемые ячейки. Например, критерий может быть выражен как 32, "32", ">32", "яблоки".

Диапазон_суммирования — фактические ячейки для суммирования.

• Ячейки в «диапазон_суммирования» суммируются, только если соответствующие им ячейки в аргументе «диапазон» удовлетворяют критерию.
• Если «диапазон_суммирования» опущен, то суммируются ячейки в аргументе «диапазон».

ПРОИЗВЕД

Перемножает числа, заданные в качестве аргументов и возвращает их произведение.

ПРОИЗВЕД(число1;число2; ...)

Число1, число2,... — от 1 до 30 перемножаемых чисел.

ОКРУГЛ

Округляет число до указанного количества десятичных разрядов.

ОКРУГЛ(число;число_разрядов)

Число — округляемое число.

Число_разрядов — количество десятичных разрядов, до которого нужно округлить число.

• Если число_разрядов больше 0, то число округляется до указанного количества десятичных разрядов справа от десятичной запятой.
• Если число_разрядов равно 0, то число округляется до ближайшего целого.

Если число_разрядов меньше 0, то число округляется слева от десятичной запятой.

НЕЧЁТ

Возвращает число, округленное до ближайшего нечетного целого.

НЕЧЁТ(число)

Число — округляемое значение.

• Если аргумент число не является числом, то функция НЕЧЁТ возвращает значение ошибки #ЗНАЧ!.
• Независимо от знака числа, округление всегда производится с избытком. Если число является нечетным целым, то округления не происходит.

ЧЁТН

Возвращает число, округленное до ближайшего четного целого. Эту функцию можно использовать при обработке объектов, которые поступают парами. Например, упаковочный ящик позволяет упаковывать по два объекта в ряд. Ящик будет заполнен, если количество объектов, округленное до ближайшего четного числа, равняется вместимости ящика.

ЧЁТН(число)

Число — это округляемое значение.

• Если аргумент число числом не является, то ЧЁТН возвращает значение ошибки #ЗНАЧ!.
• Независимо от знака числа округление производится с избытком. Если число уже является четным целым, то никакого округления не производится.

ЦЕЛОЕ

Округляет число до ближайшего меньшего целого.

ЦЕЛОЕ(число)

Число — это вещественное число, округляемое до ближайшего меньшего целого.

ОКРВВЕРХ

Возвращает результат округления с избытком до ближайшего числа, кратного точности. Например, если в значениях цен необходимо избежать рублей, а товар стоит 442 рубля, используйте формулу =ОКРВВЕРХ(442;10), чтобы округлить цену с точностью до 10 рублей.

ОКРВВЕРХ(число; точность)

Число — это округляемое значение.

Точность — это кратное, до которого требуется округлить.

• Если один из аргументов не является числом, то ОКРВВЕРХ возвращает значение ошибки #ЗНАЧ!.
• Независимо от знака числа, округление производится с избытком. Если число уже кратно точности, то округления не производится.
• Если число и точность имеют разные знаки, то функция ОКРВВЕРХ возвращает значение ошибки #ЧИСЛО!.

ОКРВНИЗ

Округляет число до кратного заданной точности с недостатком.

ОКРВНИЗ(число; точность)

Число — это округляемое числовое значение.

Точность — это кратное, до которого требуется округлить.

• Если любой из аргументов не число, то ОКРВНИЗ возвращает значение ошибки #ЗНАЧ!.
• Если число и точность имеют разные знаки, то ОКРВНИЗ возвращает значение ошибки #ЧИСЛО!.
• Независимо от знака числа, округление всегда производится с недостатком. Если число уже кратно точности, то никакого округления не производится.

ОКРУГЛВВЕРХ

Округляет число до ближайшего большего по модулю.

ОКРУГЛВВЕРХ(число;число_разрядов)

Число — любое вещественное число, которое нужно округлить с избытком.

Число_разрядов — количество цифр, до которого округляется число.

• Функция ОКРУГЛВВЕРХ подобна функции ОКРУГЛ, за тем исключением, что округление всегда производится с избытком.
• Если число_разрядов больше 0 (нуля), то число округляется с избытком до заданного количества десятичных разрядов после десятичной запятой.
• Если число_разрядов равно 0, то число округляется до ближайшего целого.
• Если число_разрядов меньше 0, то число округляется с избытком, с учетом десятичных разрядов слева от десятичной запятой.

ОКРУГЛВНИЗ

Округляет число до ближайшего меньшего по модулю значения.

ОКРУГЛВНИЗ(число;число_разрядов)

Число — любое вещественное число, которое нужно округлить с недостатком.

Число_разрядов — количество цифр, до которого округляется число.

• Функция ОКРУГЛВНИЗ подобна функции ОКРУГЛ, за тем исключением, что число всегда округляется с недостатком.
• Если число_разрядов больше 0 (нуля), то число округляется с недостатком до заданного количество десятичных разрядов после запятой.
• Если число_разрядов равно 0, то число округляется вниз до ближайшего целого.
• Если число_разрядов больше 0, то число округляется с недостатком до заданного количеств десятичных разрядов слева от запятой.

ЧИСЛКОМБ

Возвращает количество комбинаций для заданного числа объектов. Функция ЧИСЛКОМБ используется для определения числа всех возможных сочетаний объектов в группы.

ЧИСЛКОМБ(число; число_выбранных)

Число — это число элементов.

Число_выбранных — это число объектов в каждой комбинации.

Статистические функции

1) МАКС - возвращает наибольшее значение из набора значений.

МАКС(число1;число2; ...)

Число1, число2,... — от 1 до 30 чисел, среди которых требуется найти наибольшее.

МАКСА

Возвращает наибольшее значение в списке аргументов. Наряду с числовыми значениями выполняется также сравнение текстовых и логических (таких как ИСТИНА и ЛОЖЬ) значений.

МАКСА(значение1;значение2;...)

Значение1, значение2,... — от 1 до 30 значений, среди которых требуется найти наибольшее.

Аргументы, содержащие значение ИСТИНА интерпретируются как 1, аргументы, содержащие текст или значение ЛОЖЬ интерпретируются как 0 (ноль).

МИН

Возвращает наименьшее значение в списке аргументов.

МИН(число1;число2; ...)

Число1, число2,... — от 1 до 30 чисел, среди которых требуется найти наименьшее.

МИНА

Возвращает наименьшее значение в списке аргументов. Наряду с числовыми значениями выполняется также сравнение текстовых и логических, таких как ИСТИНА и ЛОЖЬ, значений.

МИНА (значение1;значение2;...)

Значение1, значение2,... — от 1 до 30 значений, среди которых требуется найти наименьшее.

Аргументы, содержащие значение ИСТИНА интерпретируются как 1, аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (нуль).

МЕДИАНА

Возвращает медиану заданных чисел. Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана.

МЕДИАНА(число1;число2;...)

Число1, число2,... — от 1 до 30 чисел, для которых определяется медиана.

МОДА

Возвращает наиболее часто встречающееся или повторяющееся значение в массиве или интервале данных. Как и функция МЕДИАНА, функция МОДА является мерой взаимного расположения значений.

МОДА(число1;число2; ...)

Число1, число2,... — от 1 до 30 аргументов, для которых вычисляется мода. Можно использовать один массив или одну ссылку на массив вместо аргументов, разделяемых точкой с запятой.

НАИБОЛЬШИЙ

Возвращает k-ое по величине значение из множества данных. Эта функция позволяет выбрать значение по его относительному местоположению. Например, функцию НАИБОЛЬШИЙ можно использовать для определения наилучшего, второго или третьего результатов тестирования в баллах.

НАИБОЛЬШИЙ(массив;k)

Массив — массив или интервал данных, для которых определяется k-ое наибольшее значение.

k — позиция (начиная с наибольшей) в массиве или интервале ячеек данных.

НАИМЕНЬШИЙ

Возвращает k-ое наименьшее значение в множестве данных. Эта функция используется для определения значения, занимающего определенное относительное положение в множестве данных.

Синтаксис

НАИМЕНЬШИЙ(массив;k)

Массив — массив или диапазон числовых данных, для которого определяется k-ое наименьшее значение.

k — позиция (начиная с наименьшей) в массиве или интервале ячеек данных.

СРОТКЛ

Возвращает среднее абсолютных значений отклонений точек данных от среднего. СРОТКЛ является мерой разброса множества данных.

СРОТКЛ(число1; число2; ...)

Число1, число2,... — это от 1 до 30 аргументов, для которых определяется среднее абсолютных отклонений. Можно использовать массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

СЧЁТ

Подсчитывает количество чисел в списке аргументов. Функция СЧЁТ используется для получения количества числовых ячеек в интервалах или массивах ячеек.

СЧЁТ(значение1; значение2; ...)

Значение1, значение2, ... — это от 1 до 30 аргументов, которые могут содержать или ссылаться на данные различных типов, но в подсчете участвуют только числа.

СЧЁТЕСЛИ

Подсчитывает количество ячеек внутри диапазона, удовлетворяющих заданному критерию.

СЧЁТЕСЛИ(диапазон;критерий)

Диапазон — диапазон, в котором нужно подсчитать ячейки.

Критерий — критерий в форме числа, выражения или текста, который определяет, какие ячейки надо подсчитывать. Например, критерий может быть выражен следующим образом: 32, "32", ">32", "яблоки".

СЧЁТЗ

Подсчитывает количество непустых значений в списке аргументов. Функция СЧЁТЗ используется для подсчета количества ячеек с данными в интервале или массиве.

СЧЁТЗ(значение1; значение2; ...)

Значение1, значение2, ... — это от 1 до 30 аргументов, количество которых требуется сосчитать. В данном случае значением считается значение любого типа, включая пустую строку (""), но не включая пустые ячейки. Если аргументом является массив или ссылка, то пустые ячейки в массиве или ссылке игнорируются.

СЧИТАТЬПУСТОТЫ

Подсчитывает количество пустых ячеек в заданном диапазоне.

СЧИТАТЬПУСТОТЫ(диапазон)

Диапазон — это диапазон, в котором требуется подсчитать количество пустых ячеек.

Ячейки с формулами, которые возвращают значение "" (пустой текст), учитываются при подсчете. Ячейки с нулевыми значениями не учитываются.

СРЗНАЧ

Возвращает среднее (арифметическое) своих аргументов.

СРЗНАЧ(число1; число2; ...)

Число1, число2, ... — это от 1 до 30 аргументов, для которых вычисляется среднее.

СРЗНАЧА

Вычисляет среднее арифметическое значений, заданных в списке аргументов.

Помимо чисел в расчете могут участвовать текст и логические значения, такие как ИСТИНА и ЛОЖЬ.

СРЗНАЧА(значение1; значение2;...)

Значение1, значение2,... — это от 1 до 30 ячеек, интервалов ячеек или значений, для которых вычисляется среднее.

Массивы и ссылки, содержащие текст, интерпретируются как 0 (ноль). Пустой текст ("") интерпретируется как 0 (ноль). Если при расчете не требуется учитывать текстовые значения, следует использовать функцию СРЗНАЧ.

Аргументы, содержащие значение ИСТИНА, интерпретируются как 1. Аргументы, содержащие значение ЛОЖЬ, интерпретируются как 0 (ноль).

Задания для самостоятельной работы

1.Запустить табличный процессор Microsoft Excel.

2.На первом листе с именем «Оценки» создать таблицу вида:

Наши рекомендации

Оценки учащихся 3 "А" класса
Предмет	Фамилия	Ученик 1	Ученик 2	Ученик 3	Уче