Решение при условных исходных данных

Некоторые задачи оптимизации можно решать с помощью логических функций, используя условие ЕСЛИ . Такие задачи будем называть задачами оптимизации при условных исходных данных. Решение этих задач начинается с оптимизации условной целевой функции . Основной логической функцией, применяемой при такой оптимизации , является логическая функция ЕСЛИ , имеющая формат записи: =ЕСЛИ (A;C3;C4), где А - логическое условие или адрес ячейки с условием; С3 - адрес ячейки , где записана целевая функция, по которой производится оптимизация при выполнении условия А; С4 - адрес ячейки , где записана целевая функция, которая оптимизируется при невыполнении условия А.

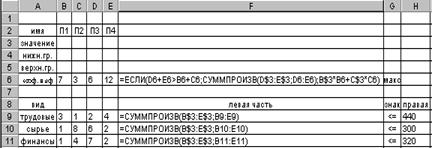
Данная функция может быть введена с помощью Мастера функций. Пример рассматриваемой задачи производственного планирования с условной целевой функцией приведен на рис. 3.23. На рис. 3.24 представлено решение данной задачи.

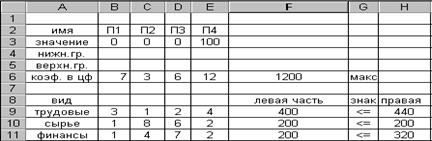
Рис.3.23

Рис. 3.24

В общем случае условные целевые функциимогут быть составными и для записи условий включать , кроме логической функции ЕСЛИ , логические функции И и ИЛИ , которые вводятся в формате И(A;B) , ИЛИ(A;B) , где А , В - назначаемые условия .

Формат записи условных вычислений при этом будет иметь вид :

=ЕСЛИ (И(A;B); адрес ЦФ1; адрес ЦФ2),

=ЕСЛИ (ИЛИ(A;B); адрес ЦФ1; адрес ЦФ2).

При решении практических задач довольно часто могут возникать логические цепочки. EXCEL допускает применение функции ЕСЛИ в цепочке до 7 раз.

Аналогично можно вводить условные ограничения. Условные исходные данные для левых частей (ЛЧ) ограничений вводятся в формате :

=ЕСЛИ (условие; адрес ЛЧ1; адрес ЛЧ2),

для правых частей (ПЧ) ограничений формат ввода аналогичен предыдущему, только вместо ЛЧ1 и ЛЧ2 записываются ПЧ1и ПЧ2.

В одной и той же задаче условия для целевой функции, левых и правых частей ограничений могут вводиться одновременно.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Вентцель Е.С. Исследование операций. Задачи, принципы, методология: учеб. пособие для вузов / Е.С. Вентцель. – М.: Дрофа, 2004.

2. Волков И.К. Исследование операций: учеб. для вузов / И.К. Волков, Е.А. Загоруйко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.

3. Гельман В.Я. Решение математических задач средствами Excel: практикум / В.Я. Гельман. – СПб.: Питер, 2003.

4. Гарбер Г.З. Основы программирования на Visual Basic в Microsoft Excel / Г.З. Гарбер. – М.: Торговый дом СПАРРК, 2004.

5. Пантелеев А.В. Методы оптимизации в примерах и задачах: учеб. пособие / А.В. Пантелеев, Т.А. Летова. – М.: Высш. шк., 2002.

6. Сафронов И.К. Visual Basic в задачах и примерах / И.К. Сафронов. – СПб.: БХВ-Петербург, 2008.

СОДЕРЖАНИЕ

1. Лабораторная работа № 1. Определение

экстремума функции методом Ньютона …………...…………1

Лабораторная работа № 2.

Этапы моделирования …………………………………….……..7

3. Лабораторная работа № 3.

Решение задач линейного программирования

с использованием средств EXСEL……..………………………13

Библиографический список…………….………………….…...33

Методические указания

к выполнению лабораторных работ по дисциплине

"Основы математического моделирования"

для студентов направления подготовки бакалавров

151900 «Конструкторско-технологическое обеспечение

машиностроительных производств»

(профиль «Технология машиностроения»)

всех форм обучения

В авторской редакции

Компьютерный набор А.В. Перовой

Подписано к изданию 30.11.2012.

Уч.-изд. л. 2,1

ФГБОУ ВПО "Воронежский государственный технический

университет"

394026 Воронеж, Московский просп., 14