Решение задач линейного программирования

С использованием средств EXСEL

Цель работы: изучить основные возможности использования табличного процессора EXСEL для решения задач линейного программирования, а также параметрического исследования с целью получить наилучший результат и его графическое представление.

Постановка задачи. Требуется определить, в каком количестве необходимо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4 для изготовления которой требуются ресурсы трех видов: трудовые ресурсы, сырье, финансы. Нормы расхода ресурсов каждого вида для выпуска единицы продукции, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в табл. 3.1. Количество расходуемых ресурсов не должно превышать имеющихся запасов.

Данная задача относится к задаче планирования при ограничениях на ресурсы, распределительного типа.

Таблица 3.1

Ресурсы	Виды продукции	Запасы ресурсов
Прод.1	Прод.2	Прод.3	Прод.4
Трудовые
Сырье
Финансы
Прибыль

Математическая модель для решения данной задачи будет иметь следующий вид:

F=7x₁+3x₂+6x₃+12x₄®max;

3x₁+x₂+2x₃+4x₄ £440;

x₁+8x₂+6x₃+2x₄ £200;

x₁+4x₂+7x₃+2x₄ £320; x_j ³0, j= .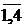

Рассмотрим последовательность работ при решении этой задачи средствами Exсel. Форма для ввода условий данной задачи может иметь следующий вид:

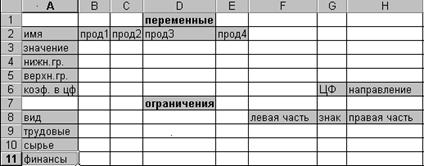
Рис. 3.1

Весь текст на рис.3.1 (и в дальнейшем) является комментарием и на решение задачи не влияет. Далее необходимо ввести в сформированную форму исходные данные (коэффициенты в целевой функции и ограничениях, а также направление оптимизации целевой функции и знаки ограничений (рис.3.2)

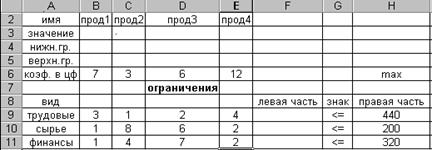
Рис.3.2

При этом ячейки B3:E3 являются изменяемыми и в них будут заноситься значения переменных.

Ввод функциональных зависимостей для целевой функции и ограничений осуществляется с использованием Мастера функций. Для этого необходимо активизировать требуемую ячейку (F6) и вызвать Мастер функций. В левой части появившегося диалогового окна нужно выбрать категорию функции Математическая, а в правом окне выделить функцию СУММПРОИЗВ и нажать клавишу ОК. Затем на экране отобразится диалоговое окно второго шага (рис. 3.3), где требуется ввести как первый (B$3:E$3), так и второй массивы (B6:E6). При вводе первого массива используются абсолютные ссылки на ячейки, при вводе второго - относительные, что в дальнейшем будет удобно при копировании формул. Во все окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, адреса которых необходимо ввести.

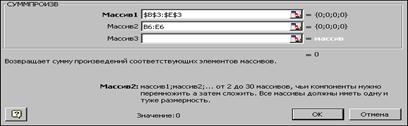Рис. 3.3

Зависимости для левых частей ограничений вводятся аналогично. При этом необходимо лишь менять адреса ячеек. Для ускорения и удобства ввода можно скопировать содержимое ячейки F6 в ячейки F9, F10 и F11 (при этом все относительные ссылки изменятся автоматически).

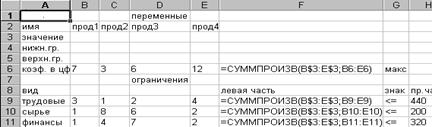
Окончательная таблица с исходными данными представлена на рис. 3.4 (для наглядности выбран режим представления формул, который использовать не обязательно).

Рис. 3.4

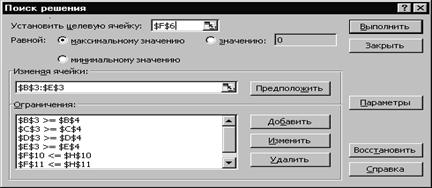
После окончания ввода исходных данных осуществляется вызов программы Поиск решения. Для этого необходимо выбрать в меню пункт Сервис (или Данные), а в нем – Поиск решения, в результате чего на экране появится окно поиска решения (рис. 3.5).

Рис. 3.5

В окне Установить целевую ячейку требуется ввести имя ячейки, в которую введена зависимость для целевой функции (в данном случае F6). В качестве направления оптимизации выбирается максимизация. В окне Изменяя ячейкивводятся адреса ячеек, соответствующих варьируемым переменным задачи (B3:E3). Далее необходимо ввести ограничения. Для добавления ограничений выбирается пункт Добавить, после чего появляется окно добавления ограничений (рис. 3.6)

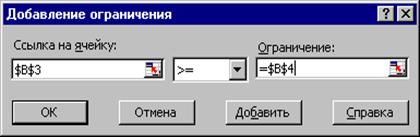Рис. 3.6

Вводятся граничные условия для переменных (Прод1 - Прод4) ³ 0: B3>= B4, C3 >= C4, D3 >= D4, E3 >= E4 (нулевые значения ячеек B4-E4 можно не устанавливать). Ограничения можно также ввести в виде B3 >= 0, C3 >= 0, D3 >= 0, E3 >= 0. Затем вводятся ограничения на ресурсы: F9 <= H9, F10 <= H10, F11 <= H11. Ограничения вводят последовательно. Сначала выбирается пункт Добавить,далее в появившихся диалоговых окнах вводится левая часть, знак и правая часть каждого ограничения. После ввода последнего ограничения и нажатия OKпроизойдет возврат в окно Поиск решения.

Заполненная в результате ввода ограничений форма поиска решений представлена на рис. 3.10. Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения.Перед началом решения необходимо установить параметры решения, для чего в окне поиска решения выбрать команду параметры.Диалоговое окно параметров поиска решения представлено на рис. 3.7.

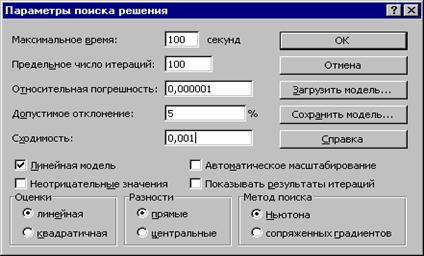
Рис. 3.7

С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. Рассмотрим наиболее важные команды, применяемые при решении конкретных задач. Команды, используемые по умолчанию, подходят для решения большей части практических задач.

Максимальное время

Служит для назначения времени в секундах, выделяемого на поиск решения задачи. В поле можно ввести время, не превышающее 32767 с (более 9 часов!). Значение 100, используемое по умолчанию, подходит для решения большинства задач.

Предельное число итераций

Служит для назначения числа итераций. Используемое по умолчанию число 100 подходит для решения большинства задач.

Относительная погрешность

Используется для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 (нуля) до 1. Низкая точность соответствует введенному числу, содержащему меньшее количество десятичных знаков, чем число, используемое по умолчанию ѕ например, 0,0001. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Допустимое отклонение

Используется для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.

Сходимость

Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков. Лучшая сходимость требует больше времени на поиск оптимального решения.

Линейная модель

Используется для решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи.