Определение экстремума функции

274 - 2012

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ

по дисциплине

"Основы математического моделирования"

для студентов направления подготовки бакалавров

151900 «Конструкторско-технологическое обеспечение

машиностроительных производств»

(профиль «Технология машиностроения»)

всех форм обучения

Воронеж 2012

Составитель канд. техн. наук А.В. Перова

УДК 532.5+533.6

Методические указания к выполнению лабораторных работ по дисциплине "Основы математического моделирования" для студентов направления подготовки бакалавров 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» (профиль «Технология машиностроения») всех форм обучения / ФГБОУ ВПО "Воронежский государственный технический университет"; сост. А.В. Перова. Воронеж, 2012. 34 с.

Методические указания включают краткие теоретические сведения по основам математического моделирования, методику и порядок выполнения лабораторных работ, снабжены перечнем рекомендуемой литературы и конкретными примерами моделирования с использованием численных методов

Издание соответствует требованиям Федерального Государственного образовательного стандарта высшего профессионального образования по направлению 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» (профиль «Технология машиностроения»), дисциплине «Основы математического моделирования».

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word XP и содержится в файле Лабораторные_ОММ.doc.

Табл. 11. Ил. 26. Библиогр.: 6 назв.

Рецензент канд. техн. наук, доц. И.А. Чечета

Ответственный за выпуск зав. кафедрой профессор А.И. Болдырев

© Перова А.В., 2012

© Оформление. ФГБОУ ВПО

"Воронежский государственный

технический университет", 2012

ЛАБОРАТОРНАЯ РАБОТА № 1

Определение экстремума функции

Методом Ньютона

Цель работы: Теоретическое изучение и получение практических навыков численного решения дифференциальных уравнений методом Ньютона.

Теоретические сведения

Если существует функция f(x) действительной переменной x непрерывная в каждой точке своей области определения и ее производная f’(x), то для приближенного решения уравнения f’(x) = 0 (т.е. для нахождения точек экстремума) можно построить приблизительный эскиз кривой y = f’(x). При этом можно найти два значения а и в, таких, что f`(a), f`(b) имеют противоположные знаки, то тогда в силу непрерывности функции и ее производной, существует корень с уравнения f`(x) = 0, отвечающий условию (рис. 1.1):

a < c < b (1.1)

В прямоугольной системе координат изобразим график функции y = f`(x) (рис.2.2). Решением уравнения y = f’(x) = 0 является точка К с координатами (x_k,0), которые необходимо определить. В точке Р, принадлежащей кривой f’(x), проведем касательную к этой кривой - прямую РТ. Проекцией точки Р на ось абсцисс является точка А с координатами (x₀,0). Можно сказать, что точка А является аппроксимацией точки К, а значение координаты x₀ - аппроксимацией корня уравнения y = f’(x) = 0. Однако из анализа рис. 1.2. можно сделать вывод, что точка Т с координатами (x₁,0) аппроксимирует корень, лежащий в точке К лучше, чем точка А.

Для точки Т можно записать следующее равенство:

OT = OA - TA = x₀ – TA (1.2)

С другой стороны для касательной РТ к кривой f`(x) справедливо:

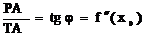(1.3)

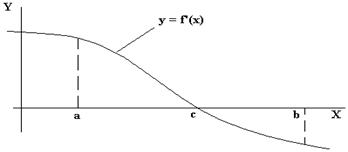Рис. 1.1. Определение корня уравнения кривой y = f’(x)

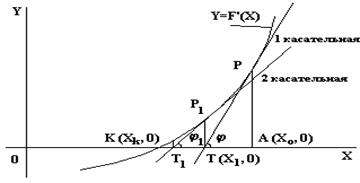Рис. 1.2. Аппроксимация корня дифференциального уравнения

Проведя преобразования выражения (1.3) можно записать:

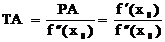(1.4)

В равенстве (1.2), заменив длину отрезка ОТ на координаты точки Т, получим:

x₁ = x₀ - TA (1.5)

Подставив в (1.5) выражение (1.4), имеем:

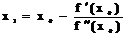(1.6)

Как видно из выражения (1.6) можно определить координату точки Т, являющейся аппроксимацией корня К с определенной точностью.

Для повышения точности аппроксимации в точке Т восстанавливают перпендикуляр к оси абсцисс (рис. 1.2), который пересекается с кривой y = f`(x) в точке P<sub>1</sub> . В этой точке строят вторую касательную к кривой f`(x), которая пересекает ось абсцисс в точке T₁. После этого вся последовательность аппроксимации повторяется:

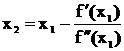(1.7)

Количество аппроксимаций зависит от требуемой степени точности результата и в общем виде записывается как:

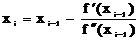(1.8)

Точность аппроксимаций определяется требуемой точностью результата по соотношению:

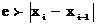(1.9)

где e - требуемая точность результата.

Если начальная аппроксимация корня выбрана неудачно, то возможно расхождение результата аппроксимаций (рис. 1.3)

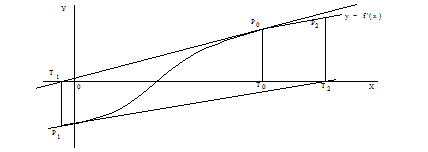
Рис.1.3. Расходящаяся аппроксимация

После того как было найдено решение x_k уравнения f`(x) = 0 определяется знак второй производной f``(x) в этой точке:

если f``(x_k) > 0, то в точке x_k достигается минимум функции f(x);

если f``(x_k) < 0, то в точке x_k достигается максимум функции f(x).

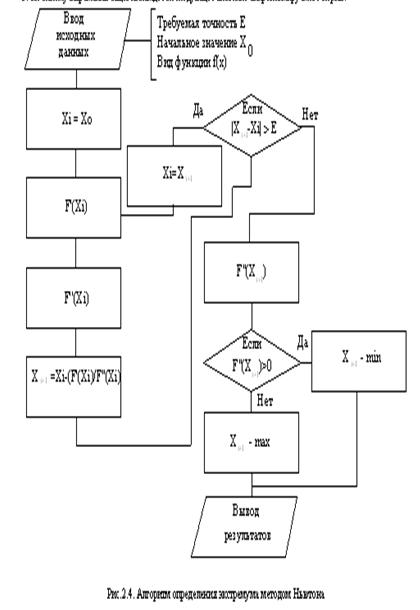
Алгоритм нахождения экстремума функции по методу Ньютона представлен на рис.2.4.

Порядок выполнения работы

1. Задание на лабораторную работу студент выбирает из табл. 1.1 в соответствии со своим порядковым номером в списке группы.

2. Опираясь на теоретические сведения студент составляет программу на любом языке программирования для решения задачи поиска экстремума функции методом Ньютона. Программа и ее результаты после отладки и проверки должны быть приложены к отчету.

3. Составляется программа построения кривой функции f(x) с масштабом, достаточным для проверки результатов расчетов по п.2 (можно использовать средства построения графиков функций других приложений - Excel или MathcadPLUS).

Содержание отчета

1. Название и цель работы, краткие теоретические сведения о методе Ньютона.

2. Заданная функция, ее первая и вторая производные.

3. Блок-система алгоритма.

4. "Листинг" программы и результаты ее выполнения.

5. Результат выполнения программы построения кривой заданной функции и сравнение полученных данных со значениями, полученными с помощью любого стандартного программного обеспечения.

6. Выводы по работе.

Контрольные вопросы

1. Поясните порядок поиска точки экстремума функции методом Ньютона.

2. Ни каких соображений выбирается значение начальной точки для аппроксимации корня?

3. По какому выражению ищется каждое последующее значение аппроксимируемого корня?

Таблица 1.1

Варианты задания для лабораторной работы № 1

№ варианта	Функция	№ варианта	Функция

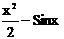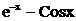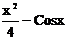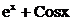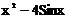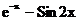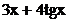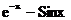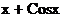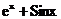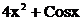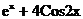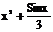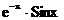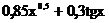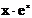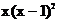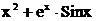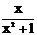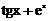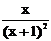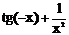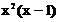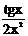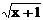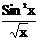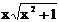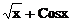Лабораторная работа № 2

Этапы моделирования

Цель работы:Теоретическое изучение основных этапов моделирования, классификации моделей и получение практических навыков создания моделей различных видов.

Теоретические сведения

При исследовании любой системы посредством математического моделирования возможно наличие многих альтернативных вариантов моделей. Каждая из них в чем-то лучше остальных, а чем-то хуже. Поэтому процесс разработки наилучшего, как правило компромиссного варианта модели, достаточно сложен. Системный подход предполагает наличие следующих этапов создания модели.

1. Синтез модели – создание возможных ее вариантов.

Различают

а) структурный синтез – разработка структуры модели: ее общего вида (например, в виде многочлена, или другой функции), определение числа параметров и т. п.

б) параметрический синтез – поиск числовых значений параметров модели либо на основании справочных данных, либо исходя из условия максимального совпадения результатов, найденных по модели, с экспериментальными.

2. Анализ модели – определение качества синтезированного варианта по критериям:

а) универсальности – полноты отображаемых свойств объекта;

б) точности – степени совпадения реальных данных с предсказанными моделью;

в) адекватности – способности правильно отображать свойства объекта;

г) экономичности – затрат на разработку и реализацию модели.

3. Выбор и принятие решений – общая оценка полезности вариантов и выбор лучшего.

В процессе перехода от словесного описания к получению результатов исследования модель объекта претерпевает следующие изменения формы своего представления.

Аналитическая модель описания – описание свойств объекта виде совокупности математических зависимостей.

Модель решения – система математического моделирования соотношений, позволяющих найти решение поставленной задачи. Существует несколько альтернативных типов этой модели:

а) аналитическая модель решения – явное выражение, позволяющее вычислить искомую величину;

б) численная модель – запись решения в виде численных схем, позволяющих найти решение в виде набора чисел;

в) имитационная модель – переложение ан язык ЭВМ набора формальных правил функционирования объекта исследования при заданном входном воздействии.

3. Алгоритмическая модель – реализация модели решения в виде алгоритма.

4. Программная модель – реализация алгоритмической модели на языке программирования.

Если при разработке какой-либо из перечисленных форм возникают альтернативные варианты моделей, то появляется необходимость в реализации процедур синтеза, анализа, принятия решения.

Пример задачи моделирования

В качестве примера разберем следующую задачу. Необходимо спроектировать емкость заданного объема V₀ оптимальных размеров: r – радиуса основания и h – высоты, имеющую форму прямого цилиндра с кромкой по периметру верхнего основания заданной высоты h₀. В качестве критериев оптимальности можно выбрать любой из параметров (или оба одновременно):

S = S_бок + 2S_осн – площадь поверхности емкости;

L = 2L_осн + (h +h₀) – длина сварного шва.

Т. к. на поверхность затрачивается листовой материал, а при сваривании расходуется электроэнергия, электроды и т. д., то в целях экономии значения обоих критериев должны быть минимальны. Кроме того , станок на котором будет реализован заказ, позволяет вырезать днище ограниченного радиуса:

R1 <r<R2.

Порядок выполнения работы

1.Задание на лабораторную работу студент выбирает из таблицы 2.1 в соответствии с номером варианта, выданным преподавателем .

2. Построить аналитическую модель описания для указанного критерия S или L, записать её в отчёт.

Проверить условие (2.7), результат записать в отчёт

В зависимости от (2.7) и разрешимости уравнения (2.6) выбрать аналитическую, численную или имитационную модель решения. Указать в отчёте обоснование выбора. Если необходима аналитическая модель, то записать (2.8) для конкретного критерия.

Составить и отладить необходимую программную модель, записать её текст в отчёт.

Получить и записать в отчёт решение задачи: оптимальное r и значение h, найденное по формуле (2.4).

Контрольные вопросы

1. Проклассифицировать полученную модель аналитического описа­ния по следующим признакам назначение степень детализации способ получения характер отображаемых свойств

2. Почему при решении задачи не использовано расчленение объ­екта как это принято при системном подходе?

3. Дать определение понятий "структура", "функция", "эффектив­ность системы".

4. Что называется аналитической, численной, имитационной моделями решения?

5. Дайте определение понятий модель и математическое моделирование.

6. Перечислите основные методы оптимизации.

Таблица 2.1

Исходные данные

№	min	V	R1	R2	h0
	S		0.5	1.5	0.05
	L		0.5	1.5	0.1
	S		1.2		0.1
	L		1.2		0.15
	S		0.5	1.5	0.15
	L		0.5	1.5	0.05
	S		1.4		0.1
	L		1.4		0.15
	S			1.8	0.25

Лабораторная работа № 3

Рис. 3.3

Зависимости для левых частей ограничений вводятся аналогично. При этом необходимо лишь менять адреса ячеек. Для ускорения и удобства ввода можно скопировать содержимое ячейки F6 в ячейки F9, F10 и F11 (при этом все относительные ссылки изменятся автоматически).

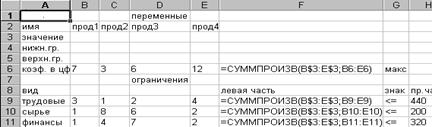
Окончательная таблица с исходными данными представлена на рис. 3.4 (для наглядности выбран режим представления формул, который использовать не обязательно).

Рис. 3.4

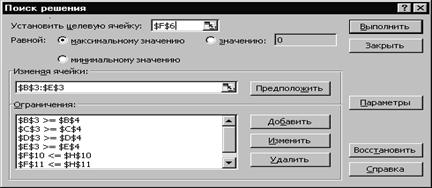
После окончания ввода исходных данных осуществляется вызов программы Поиск решения. Для этого необходимо выбрать в меню пункт Сервис (или Данные), а в нем – Поиск решения, в результате чего на экране появится окно поиска решения (рис. 3.5).

Рис. 3.5

В окне Установить целевую ячейку требуется ввести имя ячейки, в которую введена зависимость для целевой функции (в данном случае F6). В качестве направления оптимизации выбирается максимизация. В окне Изменяя ячейкивводятся адреса ячеек, соответствующих варьируемым переменным задачи (B3:E3). Далее необходимо ввести ограничения. Для добавления ограничений выбирается пункт Добавить, после чего появляется окно добавления ограничений (рис. 3.6)

Рис. 3.6

Вводятся граничные условия для переменных (Прод1 - Прод4) ³ 0: B3>= B4, C3 >= C4, D3 >= D4, E3 >= E4 (нулевые значения ячеек B4-E4 можно не устанавливать). Ограничения можно также ввести в виде B3 >= 0, C3 >= 0, D3 >= 0, E3 >= 0. Затем вводятся ограничения на ресурсы: F9 <= H9, F10 <= H10, F11 <= H11. Ограничения вводят последовательно. Сначала выбирается пункт Добавить,далее в появившихся диалоговых окнах вводится левая часть, знак и правая часть каждого ограничения. После ввода последнего ограничения и нажатия OKпроизойдет возврат в окно Поиск решения.

Заполненная в результате ввода ограничений форма поиска решений представлена на рис. 3.10. Решение задачи производится сразу же после ввода данных, когда на экране находится диалоговое окно Поиск решения.Перед началом решения необходимо установить параметры решения, для чего в окне поиска решения выбрать команду параметры.Диалоговое окно параметров поиска решения представлено на рис. 3.7.

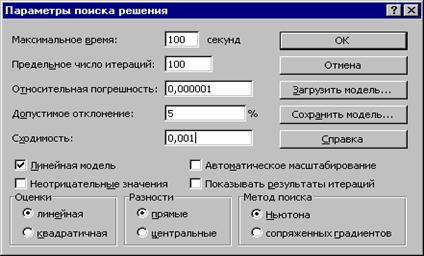
Рис. 3.7

С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. Рассмотрим наиболее важные команды, применяемые при решении конкретных задач. Команды, используемые по умолчанию, подходят для решения большей части практических задач.

Максимальное время

Служит для назначения времени в секундах, выделяемого на поиск решения задачи. В поле можно ввести время, не превышающее 32767 с (более 9 часов!). Значение 100, используемое по умолчанию, подходит для решения большинства задач.

Предельное число итераций

Служит для назначения числа итераций. Используемое по умолчанию число 100 подходит для решения большинства задач.

Относительная погрешность

Используется для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 (нуля) до 1. Низкая точность соответствует введенному числу, содержащему меньшее количество десятичных знаков, чем число, используемое по умолчанию ѕ например, 0,0001. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Допустимое отклонение

Используется для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.

Сходимость

Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков. Лучшая сходимость требует больше времени на поиск оптимального решения.

Линейная модель

Используется для решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи.

Значения не отрицательны

Позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение.

Остальные команды будут рассмотрены позже при изучении соответствующих классов задач.

Для решения задачи линейного программирования необходимо установить флажок Линейная модельв окне Параметры поиска решения, что обеспечит использование симплексного метода. Далее после выбора OKпроизойдет возврат в окно Поиск решения.Запуск процесса решения задачи осуществляется командой Выполнить.

Решение задачи занимает несколько секунд, после чего на экране появляется диалоговое окно Результаты поиска решения. При решении рассматриваемой задачи производственного планирования в окне появится сообщение о том, что решение найдено. В данном окне предоставляется возможность или сохранить найденное решение во влияющих ячейках модели, или восстановить исходные данные. Для этого необходимо отметить нужный пункт.

Результирующие значения всех переменных записываются в ячейки B3-E3 исходной задачи. Соответствующее значение целевой функции заносится в ячейку F6, а значения левых частей ограничений – в ячейки F9-F11. Таблица с результатами решения задачи представлена на рис. 3.8.

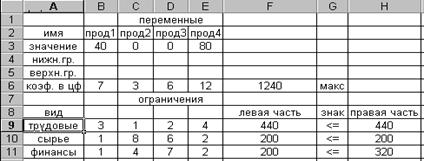
Рис. 3.8

Рис. 3.8 показывает, что в оптимальном решении

Прод1 = В3 = 40;

Прод2 = С3 = 0;

Прод3 = D3 = 0;

Прод4 = Е3 = 80.

При этом максимальная прибыль будет составлять F6 = 1240, а количество использованных ресурсов равно:

трудовых = F9 = 440,

сырья = F10 = 200,

финансов = F11 = 200.

Однако решение задачи находится не всегда. Если условия задачи несовместны, на экране появится надпись - Поиск не может найти подходящего решения. Если целевая функция не ограничена, то в окне результатов поиска решения появится сообщение: Значения целевой функции не сходятся.

Кроме этого, из окна Результаты поиска решения возможно создание отчётов трех типов: по результатам, устойчивости и пределам, каждый из которых записывается на отдельном листе. Отчеты используются при анализе полученного оптимального решения. Рассмотрим более подробно их содержание.

Отчет по результатам(рис. 3.9) состоит из трех таблиц. В таблице 1 (целевая ячейка) приведены сведения о целевой функции, в столбце "Исходно" - указывается значение целевой функции до вычислений, "Результат" - указывается значение целевой функции после вычислений.

Таблица 2 (изменяемые ячейки) содержит сведения о значениях искомых переменных, до и после решения задачи.

Таблица 3 (ограничения) показывает результаты оптимального решения для ограничений и для граничных условий. Здесь в графе "Формула" приведены зависимости, которые были введены в диалоговом окне "Поиск решения"); в графе "Разница" показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе "Состояние" указывается связанное; при неполном использовании ресурса в этой графе указывается не связан.

Рис.3.9

Отчет по устойчивости(рис. 3.10) состоит из двух таблиц.

В таблице 1 (изменяемые ячейки)приводятся следующие значения для переменных:

- результат решения задачи;

- редуцированная стоимость, т.е. дополнительные двойственные переменные v_j, которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

- коэффициенты целевой функции;

-предельные значения приращения коэффициентов Dc_j целевой функции при которых сохраняется набор переменных, входящих в оптимальное решение.

В таблице 2 (ограничения) приводятся аналогичные значения для ограничений:

- величины использованных ресурсов;

- теневые цены, т.е. двойственные оценки y_i, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;

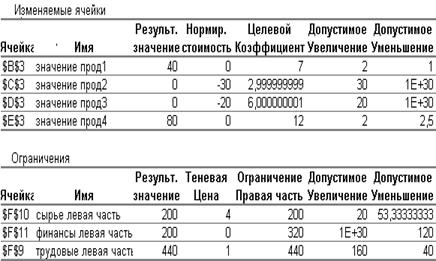
- значения приращения ресурсов Db_i, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.

Рис. 3.10

Отчет по пределам(рис. 3.11) показывает, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения:

- рассматриваются значения x_j в оптимальном решении;

- рассматриваются нижние пределы изменения значений x_j.

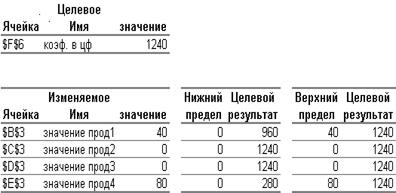Кроме этого, в отчете указаны значения целевой функции при выпуске данного типа продукции на нижнем пределе. Далее приводятся верхние пределы изменения x_j и значения целевой функции при выпуске продукции, вошедшей в оптимальное решение на верхних пределах.

Рис. 3.11

Параметрический анализ

Под параметрическим анализом будем понимать решение задачи оптимизации при различных значениях того параметра, который ограничивает улучшение целевой функции.

Параметрический анализ будем выполнять для рассматриваемой задачи производственного планирования, решая её при различных значениях имеющегося сырья. Составим таблицу вариантов:

Вариант
Сырье

Для выполнения параметрических расчетов в таблице с результатами решения задачи (рис. 3.8) необходимо удалить результат решения, находящийся в ячейках B3:E3. Далее решить задачу для первого варианта по описанной выше схеме, предварительно введя в ячейку H10 значение 100. После решения задачи в диалоговом окне Результаты поиска решения выбирается команда Сохранить сценарий. При этом на экране появится диалоговое окно Сохранение сценария (рис. 3.16). В появившемся диалоговом окне необходимо ввести имя сценария “Сырье=100” и подтвердить ввод выбором кнопки OK.

Рис. 3.16

Результат решения задачи для данного варианта представлен на рис. 3.17. Далее необходимо аналогично решить задачу для всех оставшихся вариантов, последовательно вводя в ячейку H10 значения 150, 200, 250, 300. При этом нужно сохранять каждый сценарий и вводить его имя, соответствующее текущему значению сырья.

Рис. 3.17

Для представления результатов решения вызывается пункт меню Сервис, Сценарии (или Анализ данных, «Что? Если?»)и в появившемся диалоговом окне Диспетчер сценариев(рис. 3.18) выбирается пункт От

чет.

Рис. 3.18

При выборе в диалоговом окне Отчет по сценарию (рис. 3.19) типа отчета Структурасоздается итоговый сценарий (рис. 3.20), который размещается на отдельном листе с названием “Структура сценария”.

Рис. 3.19

Рис. 3.20

Для удобства дальнейшей работы полученный сценарий можно отредактировать и представить следующем виде:

Рис. 3.21

Для наглядного представления результатов параметрического анализа построим гистограммы:

Рис.3.22

Решения по заказу

При решении по заказу пользователь задает значения тех величин, которые он хотел бы видеть в оптимальном решении. Такие задачи могут быть трех видов:

назначение величины целевой функции;

назначение величин искомых переменных;

назначение величин используемых ресурсов.

Рассмотрим возможные варианты на примере решаемой задачи производственного планирования.

В первом случае для получения результата необходимо в ячейку, соответствующую целевой функции (F6), ввести требуемую величину, а затем, вызвав программу Поиск решения, решить задачу по рассмотренной выше схеме.

Во втором случае в ячейки B4:D4, соответствующие нижним границам значений переменных задачи, вводятся требуемые значения переменных. Далее вызывается программа Поиск решения, в появившемся диалоговом окне осуществляется переход к окну Ограничения,курсор устанавливается на ограничение $B$3>=$B$4, вызывается команда Изменить и вместо знака >= вводится знак =. Аналогичные изменения производятся и с ограничениями $C$3>=$C$4, $D$3>=$D$4, $E$3>=$E$4, после чего осуществляется решение задачи.

В третьем случае в таблицу с исходными данными вводятся требуемые значения используемых ресурсов (при этом необходимое значение для трудовых ресурсов заносится в ячейку F9, для сырья - в ячейку F10, для финансов - в ячейку F11) и задача решается обычным образом.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Вентцель Е.С. Исследование операций. Задачи, принципы, методология: учеб. пособие для вузов / Е.С. Вентцель. – М.: Дрофа, 2004.

2. Волков И.К. Исследование операций: учеб. для вузов / И.К. Волков, Е.А. Загоруйко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.

3. Гельман В.Я. Решение математических задач средствами Excel: практикум / В.Я. Гельман. – СПб.: Питер, 2003.

4. Гарбер Г.З. Основы программирования на Visual Basic в Microsoft Excel / Г.З. Гарбер. – М.: Торговый дом СПАРРК, 2004.

5. Пантелеев А.В. Методы оптимизации в примерах и задачах: учеб. пособие / А.В. Пантелеев, Т.А. Летова. – М.: Высш. шк., 2002.

6. Сафронов И.К. Visual Basic в задачах и примерах / И.К. Сафронов. – СПб.: БХВ-Петербург, 2008.

СОДЕРЖАНИЕ

1. Лабораторная работа № 1. Определение

экстремума функции методом Ньютона …………...…………1

Лабораторная работа № 2.

Этапы моделирования …………………………………….……..7

3. Лабораторная работа № 3.

Решение задач линейного программирования

с использованием средств EXСEL……..………………………13

Библиографический список…………….………………….…...33

Методические указания

к выполнению лабораторных работ по дисциплине

"Основы математического моделирования"

для студентов направления подготовки бакалавров

151900 «Конструкторско-технологическое обеспечение

машиностроительных производств»

(профиль «Технология машиностроения»)

всех форм обучения

В авторской редакции

Компьютерный набор А.В. Перовой

Подписано к изданию 30.11.2012.

Уч.-изд. л. 2,1

ФГБОУ ВПО "Воронежский государственный технический

университет"

394026 Воронеж, Московский просп., 14

274 - 2012

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторных работ

по дисциплине

"Основы математического моделирования"

для студентов направления подготовки бакалавров

151900 «Конструкторско-технологическое обеспечение

машиностроительных производств»

(профиль «Технология машиностроения»)

всех форм обучения

Воронеж 2012

Составитель канд. техн. наук А.В. Перова

УДК 532.5+533.6

Методические указания к выполнению лабораторных работ по дисциплине "Основы математического моделирования" для студентов направления подготовки бакалавров 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» (профиль «Технология машиностроения») всех форм обучения / ФГБОУ ВПО "Воронежский государственный технический университет"; сост. А.В. Перова. Воронеж, 2012. 34 с.

Методические указания включают краткие теоретические сведения по основам математического моделирования, методику и порядок выполнения лабораторных работ, снабжены перечнем рекомендуемой литературы и конкретными примерами моделирования с использованием численных методов

Издание соответствует требованиям Федерального Государственного образовательного стандарта высшего профессионального образования по направлению 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» (профиль «Технология машиностроения»), дисциплине «Основы математического моделирования».

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word XP и содержится в файле Лабораторные_ОММ.doc.

Табл. 11. Ил. 26. Библиогр.: 6 назв.

Рецензент канд. техн. наук, доц. И.А. Чечета

Ответственный за выпуск зав. кафедрой профессор А.И. Болдырев

© Перова А.В., 2012

© Оформление. ФГБОУ ВПО

"Воронежский государственный

технический университет", 2012

ЛАБОРАТОРНАЯ РАБОТА № 1

Определение экстремума функции

Методом Ньютона

Цель работы: Теоретическое изучение и получение практических навыков численного решения дифференциальных уравнений методом Ньютона.

Теоретические сведения

Если существует функция f(x) действительной переменной x непрерывная в каждой точке своей области определения и ее производная f’(x), то для приближенного решения уравнения f’(x) = 0 (т.е. для нахождения точек экстремума) можно построить приблизительный эскиз кривой y = f’(x). При этом можно найти два значения а и в, таких, что f`(a), f`(b) имеют противоположные знаки, то тогда в силу непрерывности функции и ее производной, существует корень с уравнения f`(x) = 0, отвечающий условию (рис. 1.1):

a < c < b (1.1)

В прямоугольной системе координат изобразим график функции y = f`(x) (рис.2.2). Решением уравнения y = f’(x) = 0 является точка К с координатами (x_k,0), которые необходимо определить. В точке Р, принадлежащей кривой f’(x), проведем касательную к этой кривой - прямую РТ. Проекцией точки Р на ось абсцисс является точка А с координатами (x₀,0). Можно сказать, что точка А является аппроксимацией точки К, а значение координаты x₀ - аппроксимацией корня уравнения y = f’(x) = 0. Однако из анализа рис. 1.2. можно сделать вывод, что точка Т с координатами (x₁,0) аппроксимирует корень, лежащий в точке К лучше, чем точка А.

Для точки Т можно записать следующее равенство:

OT = OA - TA = x₀ – TA (1.2)

С другой стороны для касательной РТ к кривой f`(x) справедливо:

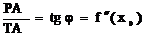(1.3)

Рис. 1.1. Определение корня уравнения кривой y = f’(x)