Уравнение нелинейной регрессии

y = b*m^x , (2)

Функция (2) устанавливает зависимость значений Y от независимых значений Х (аргументов). Значения m являются основанием для возведения в степень x, а значения b постоянны. Значения y, x и m могут быть векторами.

Функция ЛГРФПРИБЛ расчитывает массив {mn;mn-1;...;m1;b}.

Формат фукции (синтаксис):

ЛГРФПРИБЛ(известные_значения_y;известные_значения_x;конст;статистика)

Известные_значения_y - это множество значений y, которые уже известны для соотношения y = b*m^x. На рисунке 3 дан пример расчета исходных данных по экспоненте.

Рис.3.

Множественная Линейная Регрессия

y = m1*x1 + m2*x2 + m3*x3 + m4*x4 + b

Синтаксис

ЛИНЕЙН (известные_значения_y;известные_значения_x;конст;статистика)

возвращает параметры уравнения множественной регрессии:

y = m1*x1 + m2*x2 + m3*x3 + m4*x4 + b

Перед расчетом коэффициентов необходимо сформировать (построить) последовательный массив из переменных Х-ов. Переменные Х₁ ,Х₂ … должны быть в столцах А,В,С… .

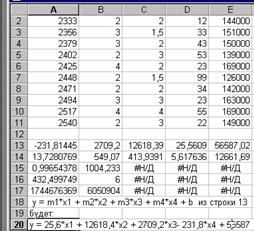
На рисунке 4 представлена задача нахождения уравнения множественной регрессии по четырем независимым переменным. Для вывода данных результата расчета, т.е. расчета дополнительной регрессии необходимо выделить нужное количество столбцов и строк для данных расчета (5х10 для рассматриваемого примера). Расчет производится Нажатием Ctrl + Shift +Enter. Данные выбираются в обратной

Рис. 4.

последовательности соответствий переменных и ячеек: X4 – A, , Х3 – B X2 – C, Х1 – D, Y – E. Полученное уравнение y = 25,6*x1 + 12618,4*x2 + 2709,2*x3- 231,8*x4 + 56587 дает возможность вычислять значения Yi по всему массиву значений Х-ов. Более подробное описание использования функций Ехcеl смотри в Справкепрограммы.

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Т

Д

В

Т

Д

В

Т

Д

В

Т

Д

В

Т

Д

В

Т

Д

В

Т

Д

В

Т

Д

В

Т

Д

В

-1

-2

Проверка полученных уравнений регрессии

Проверка уравнений и получения значений погрешностей определяется обратным пересчетом:

· в полученное уравнение подставляются исходные значения массива Х-ов (например давления, влажности) и получаются расчетные значения массива определяемого параметра Y (например температуры),

· по массиву Y - ов определяют средние значение Y_{ср. рас.}

· определяется абсолютное значение разности (отклонения) расчетных и текущих (действительных) значений Y_откл. = │ Y_{ср. рас. –} Y_{ср. дейс.}│,

· определяется относительна (действительному значению) погрешность

Y_отн. =( Y_откл./ Y_{ср. дейс.}) * 100%,

Допустимой считается погрешность 4… 6 %. При большем значении изменяют модель (уравнение) или количество переменных Х.