Алгоритм задачи решения уравнений методом дихотомии.
Задача. Уточнить корень уравнения sin2x-lnx=0 ,если функция f(x)=sin2x-lnx непрерывна на отрезке [1;1,5 ] и имеет на нем единственный корень.
Решение проведем, используя формулы (1) и (2).
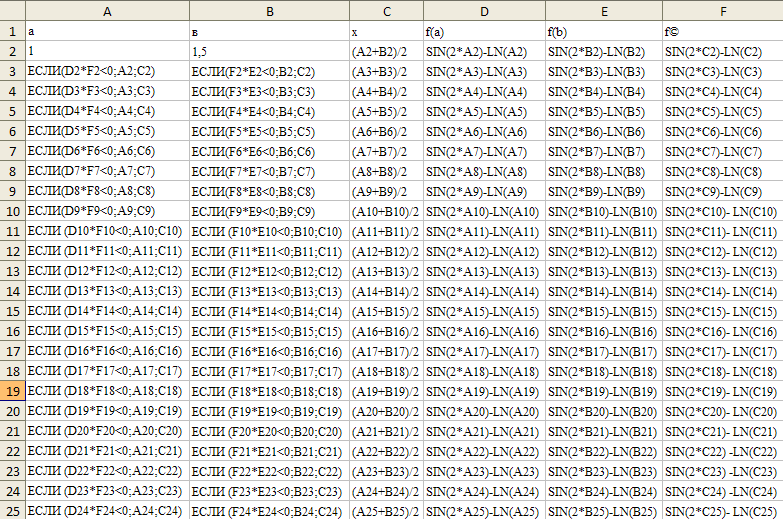
Результат:
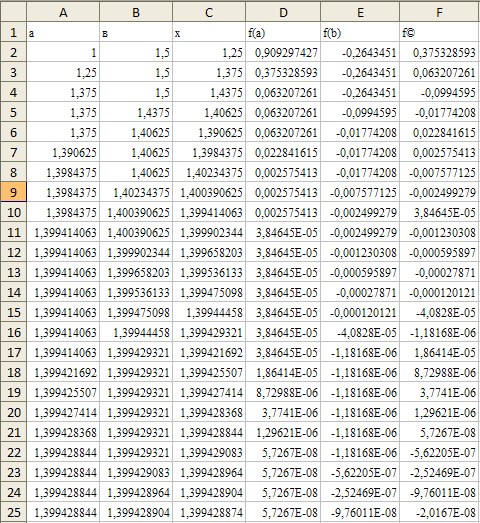
Корень: x=1,399429.
Алгоритм уточнения корня уравнения методом простой итерации.
Задача. Уточнить корень уравнения x*x*x – x – 1, отделенный на отрезке [1, 2] методом простой итерации с точностью 10-4.
Решение. Приведем уравнение к итерационному виду. Учитывая |f’(x)|=11, примем q=7. Используя формулы (3) и (4), получим:
x n+1 = x n – f(x)/7
| A | B | C | D | E | |
| МЕТОД ИТЕРАЦИЙ | |||||
| № | x | f(x) | f1(x) | 1-f(x)/k | |
| =B5*B5*B5-B5-1 | =3*B5*B5-1 | =ABS(1-D5/F$2) | |||
| =B5+0,1 | =B6*B6*B6-B6-1 | =3*B6*B6-1 | =ABS(1-D6/F$2) | ||
| =B6+0,1 | =B7*B7*B7-B7-1 | =3*B7*B7-1 | =ABS(1-D7/F$2) | ||
| =B7+0,1 | =B8*B8*B8-B8-1 | =3*B8*B8-1 | =ABS(1-D8/F$2) | ||
| =B8+0,1 | =B9*B9*B9-B9-1 | =3*B9*B9-1 | =ABS(1-D9/F$2) | ||
| =B9+0,1 | =B10*B10*B10-B10-1 | =3*B10*B10-1 | =ABS(1-D10/F$2) | ||
| =B10+0,1 | =B11*B11*B11-B11-1 | =3*B11*B11-1 | =ABS(1-D11/F$2) | ||
| =B11+0,1 | =B12*B12*B12-B12-1 | =3*B12*B12-1 | =ABS(1-D12/F$2) | ||
| =B12+0,1 | =B13*B13*B13-B13-1 | =3*B13*B13-1 | =ABS(1-D13/F$2) | ||
| =B13+0,1 | =B14*B14*B14-B14-1 | =3*B14*B14-1 | =ABS(1-D14/F$2) | ||
| =B14+0,1 | =B15*B15*B15-B15-1 | =3*B15*B15-1 | =ABS(1-D15/F$2) |
продолжение таблицы
| F | G | H | |
| K | |||
| xx | f(xx) | g=x-f(x)/k | |
| =F5*F5*F5-F5-1 | =F5-G5/F$2 | ||
| =H5 | =F6*F6*F6-F6-1 | =F6-G6/F$2 | |
| =H6 | =F7*F7*F7-F7-1 | =F7-G7/F$2 | |
| =H7 | =F8*F8*F8-F8-1 | =F8-G8/F$2 | |
| =H8 | =F9*F9*F9-F9-1 | =F9-G9/F$2 | |
| =H9 | =F10*F10*F10-F10-1 | =F10-G10/F$2 | |
| =H10 | =F11*F11*F11-F11-1 | =F11-G11/F$2 | |
| =H11 | =F12*F12*F12-F12-1 | =F12-G12/F$2 | |
| =H12 | =F13*F13*F13-F13-1 | =F13-G13/F$2 | |
| =H13 | =F14*F14*F14-F14-1 | =F14-G14/F$2 | |
| =H14 | =F15*F15*F15-F15-1 | =F15-G15/F$2 | |
| =H15 | =F16*F16*F16-F16-1 | =F16-G16/F$2 | |
| =H16 | =F17*F17*F17-F17-1 | =F17-G17/F$2 |
Результат:
| A | B | C | D | E | F | G | H | |
| МЕТОД ИТЕРАЦИЙ | ||||||||
| K | ||||||||
| № | x | f(x) | f1(x) | 1-f(x)/k | xx | f(xx) | g=x-f(x)/k | |
| -1 | 0,71429 | -1 | 1,143 | |||||
| 1,1 | -0,769 | 2,63 | 0,62429 | -0,65015 | 1,236 | |||
| 1,2 | -0,472 | 3,32 | 0,52571 | -0,34872 | 1,286 | |||
| 1,3 | -0,103 | 4,07 | 0,41857 | -0,16099 | 1,309 | |||
| 1,4 | 0,344 | 4,88 | 0,30286 | -0,06791 | 1,318 | |||
| 1,5 | 0,875 | 5,75 | 0,17857 | -0,02741 | 1,322 | |||
| 1,6 | 1,496 | 6,68 | 0,04571 | -0,01085 | 1,324 | |||
| 1,7 | 2,213 | 7,67 | 0,09571 | -0,00426 | 1,324 | |||
| 1,8 | 3,032 | 8,72 | 0,24571 | -0,00167 | 1,325 | |||
| 1,9 | 3,959 | 9,83 | 0,40429 | -0,00065 | 1,325 | |||
| 0,57143 | -0,00026 | 1,325 | ||||||
| -1E-04 | 1,325 | |||||||
| -3,9E-05 | 1,325 |
Алгоритм решения на языке TMTPascal.
Задача. Решить уравнение итерационного вида x-0.5*(x*x*x-sin(x))=0, уточнить корень на отделенном отрезке.
program metod_prostoy_iterazii;
var a,b,x,y,eps: real;
i: byte;
BEGIN
write('Vvedite tocnost:','eps=');read(eps);
write('a=');read(a);
write('b=');read(b);
x:=a+0.1;
i:=0;
while abs(y-x)>=eps do
begin
i:=i+1;
y:=x-0.5*(x*x*x-sin(x));
x:=y;
end;
writeln('x=',x:10:3);
write('shag:',i);
END.
Алгоритм уточнения корня уравнения методом Ньютона.
Задача. Уточнить корень уравнения sin2x-lnx=0 методом Ньютона на отрезке [1,3;1,5] с точностью 10-4.
Решение. Для проверки точности положим m=2,4. Используя формулы (5) и (6), получим:
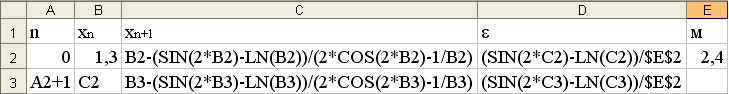
Результат:
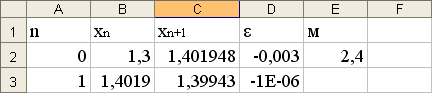
Корень: x=1,39943.
Алгоритм уточнения корня уравнения методом хорд.
Задача. Уточнить корень уравнения sin2x-lnx=0 методом хорд на отрезке [1,3;1,5] с точностью 10-4.
Решение. Определим точки с=1,5 и x0=1,3. Используя формулы (6), (7), (8) и принимая m=2,4, получим:

Результат:
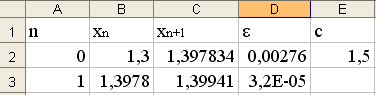
Корень: x=1,3994104.
Практическая часть
План решения нелинейного уравнения
Отделить корни, выбрать один отрезок длинной 1 или менее.
1. Представить уравнение в виде f(x)=0, найти отрезок (а : б).
2. Выбрать метод уточнения, обосновать выбор (f’, f” в точках (а : б); определить неподвижную точку метода хорд и точку касания).
3. Составить расчетную формулу метода.
4. Выполнить расчеты по формуле; построить графики.
5. Ответ (последовательность приближенных решений с округленным последним значением).
Задание 1. Отделить корни и уточнить методом хорд, методом секущих, методом итераций с точностью 0,001.
| N | f(x) | N | f(x) |
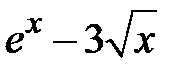 | 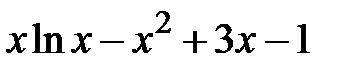 | ||
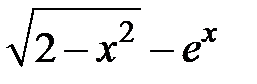 | 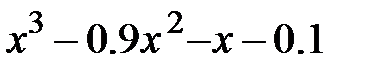 | ||
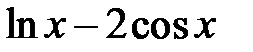 | 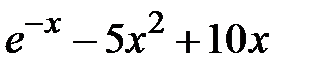 | ||
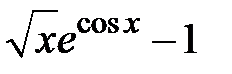 | 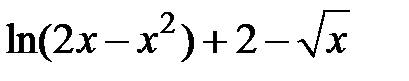 | ||
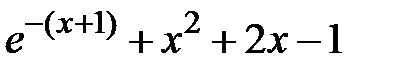 | 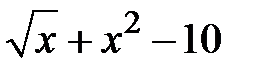 |
Задание 2. Уточнить корень уравнений g(x)=0, отделенный на указанном отрезке, комбинированным методом
| № варианта | g(x) | [a, b] |
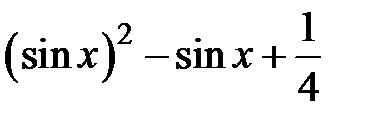 | 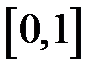 | |
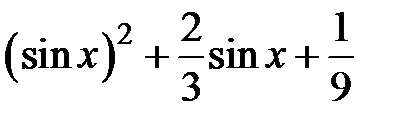 | 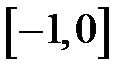 | |
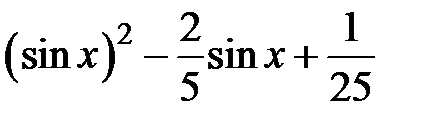 | 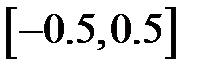 | |
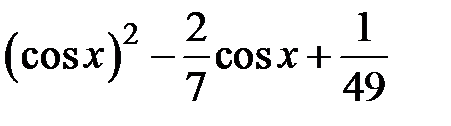 | 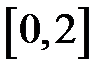 | |
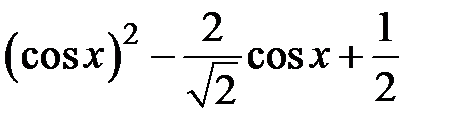 | 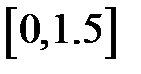 | |
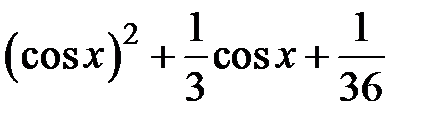 | 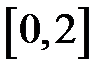 | |
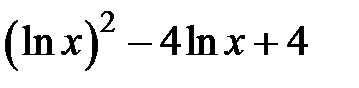 | [5,25] | |
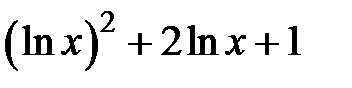 | [0.1,10] | |
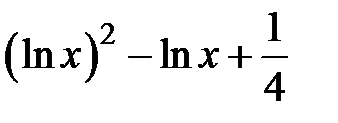 | [0.1,2] | |
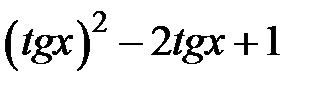 | 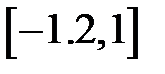 | |
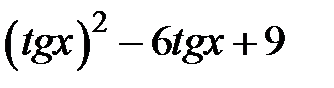 | 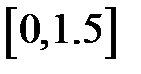 | |
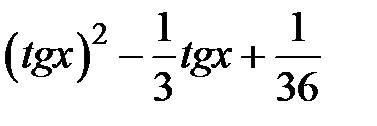 | 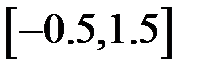 | |
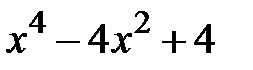 | [0,3] | |
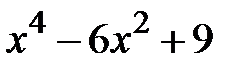 | [0,2] | |
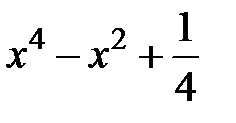 | [0,3] | |
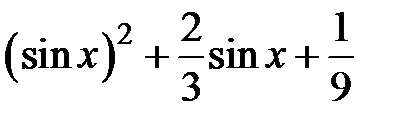 | 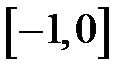 | |
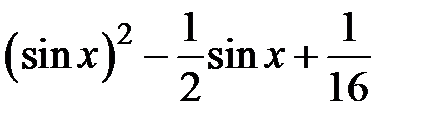 | 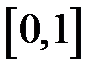 | |
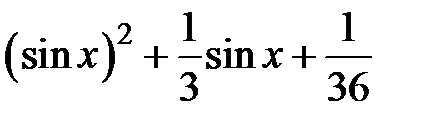 | 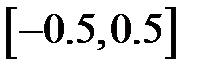 | |
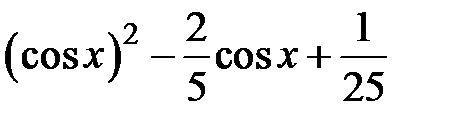 | 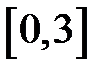 | |
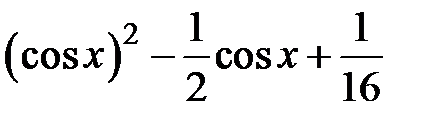 | 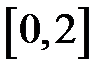 | |
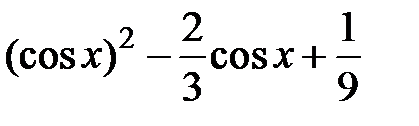 | 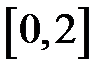 | |
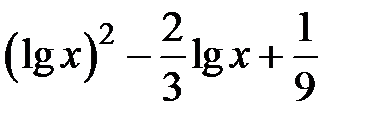 | [0.001,3] | |
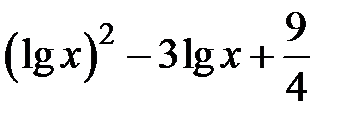 | [0.1,35] | |
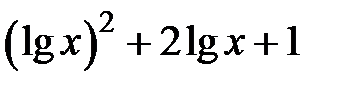 | [0.01,3] | |
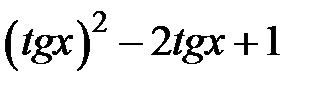 | 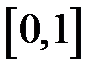 | |
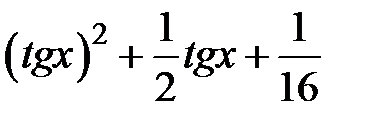 | [-0.5,1.5] | |
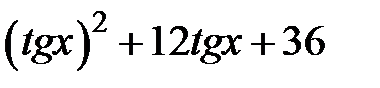 | [-1.5,0] | |
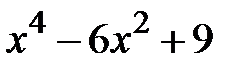 | [1,3] | |
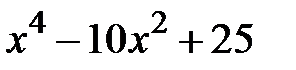 | [0,3] | |
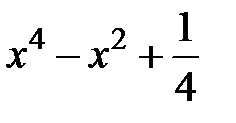 | [0,5] |
Вопросы к защите лабораторной работы №2
«Решение нелинейных уравнений».
1. Постановка задачи решения нелинейных уравнений. Основные этапы решения задачи.
2. Итерационное уточнение корней: порядок сходимости метода.
3. Метод бисекции: описание метода, скорость сходимости, критерий окончания.
4. Метод простой итерации решения нелинейного уравнения: описание метода, условие и скорость сходимости, критерий окончания, геометрическая иллюстрация, приведение к виду, удобному для итераций.
5. Метод Ньютона решения нелинейного уравнения: описание метода, теорема о сходимости, критерий окончания, геометрическая иллюстрация.
6. Метод секущих: описание метода, теорема о сходимости, критерий окончания, геометрическая иллюстрация.
ЛАБОРАТОРНАЯ РАБОТА №3
