С помощью каких команд строятся графики на плоскости и в пространстве? Какие аргументы имеют эти команды?
Лабораторная работа №3
"Построение графиков"
Преподаватель: Выборнова Е. И.
Выполнил работу: Певцова В. Ю.
а=7, b=8, с = 7
Группа: Э-08
Смоленск 2010 г.
Лабораторная работа №3
Выполнил студент Певцова Виктория Юрьевна
Файл с заданиями сохранен по именем Певцова_3
Контрольные задания
Задание 1
Построить на отдельных рисунках графики функций Бесселя первого рода Jn(x) для различных ее номеров n в интервале –20<x<20. Функции Бесселя вызываются командой BesselJ(n,x), где n – номер функции Бесселя, x – независимая переменная. Построить первые 6 функций Бесселя для n=0,1,2,3,4,5,6. Как они выглядят и чем отличаются друг от друга? Сделать подписи осей курсивом.
> plot(BesselJ(0,x),x=-20..20, labels=[x,Jn], labelfont=[TIMES,ITALIC,12]);
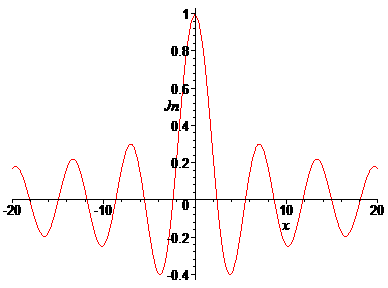
> plot(BesselJ(1,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);
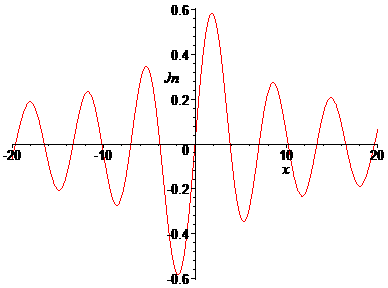
> plot(BesselJ(2,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);
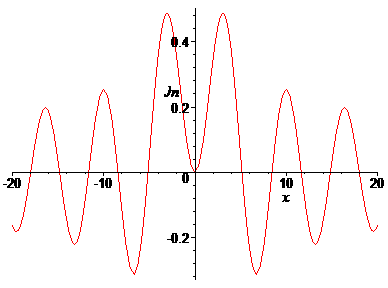
> plot(BesselJ(3,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);
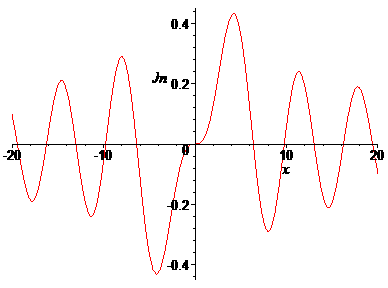
> plot(BesselJ(4,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);
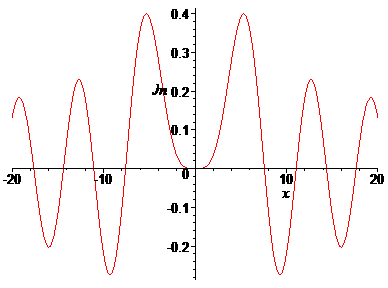
> plot(BesselJ(5,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);
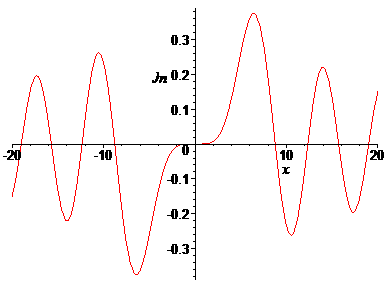
> plot(BesselJ(6,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);
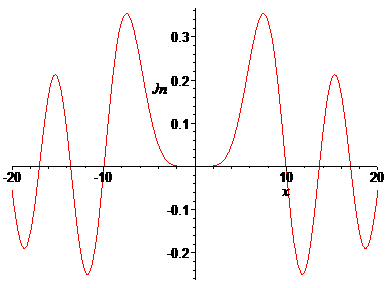
Задание 2
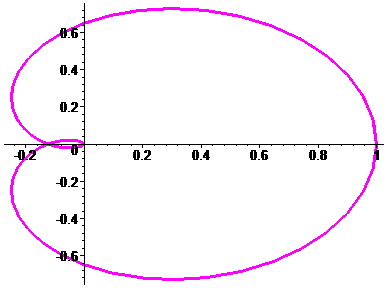
1. Построить график функции 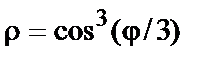 в полярных координатах при 0<j<4p. Используйте цвет линии под названием magenta, установите толщину линии 3.
в полярных координатах при 0<j<4p. Используйте цвет линии под названием magenta, установите толщину линии 3.
> plot(cos(x/3)^3, x=0..4*Pi, coords=polar, color=magenta, thickness=3);
Задание 3
Построить на одном рисунке графики функции  и ее асимптот
и ее асимптот 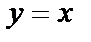 и
и 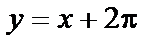 . Установить следующие параметры: цвет основной линии – голубой, асимптот – красный (установлен по умолчанию, поэтому его можно не изменять); толщина основной линии – 3, асимптоты – обычной; масштаб по координатным осям – одинаковый. Сделать надписи: какая функция относится к какой линии. Указание: использовать для преобразования в текст формул команду convert, а для построения графиков и надписей команды textplot и display из пакета plots
. Установить следующие параметры: цвет основной линии – голубой, асимптот – красный (установлен по умолчанию, поэтому его можно не изменять); толщина основной линии – 3, асимптоты – обычной; масштаб по координатным осям – одинаковый. Сделать надписи: какая функция относится к какой линии. Указание: использовать для преобразования в текст формул команду convert, а для построения графиков и надписей команды textplot и display из пакета plots
Задание 4
Построить график функции 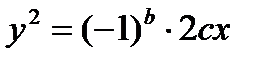 .
.
> with(plots):
implicitplot(y^2=(-1)^8*14*x, x=-20..20, y=-16..16,color=blue, thickness=2, title="Парабола");
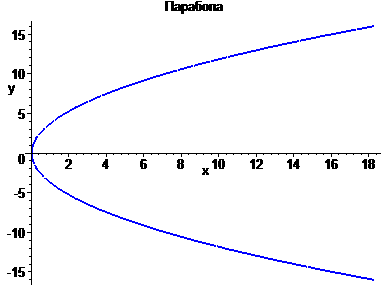
Задание 5
Построить график поверхности и определить ее вид 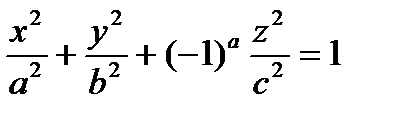 .
.
> with(plots): implicitplot3d((x^2/49)+(y^2/64)+(-1)^7*(z^2/49)=0, x=-5..5, y=-5..5,z=-5...5,scaling=CONSTRAINED,title="Конус");
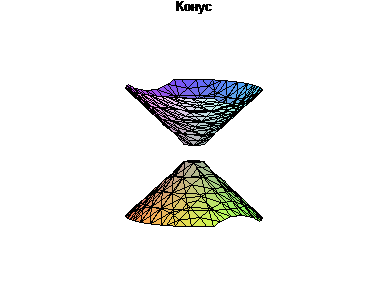
Задание 6
Построить в одной системе координат графики поверхностей 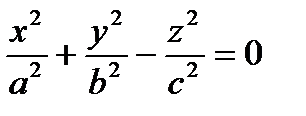 и
и 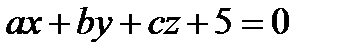 и определить их вид. Пользуясь возможностями Maple, настроить оптимальное изображение.
и определить их вид. Пользуясь возможностями Maple, настроить оптимальное изображение.
> with(plots): implicitplot3d({7*x+8*y+7*z+5=0,x^2/49+y^2/64-z^2/49=0}, x=-5..5, y=-5..5,z=-5...5,scaling=CONSTRAINED,title="Плоскость и конус");

Задание 7
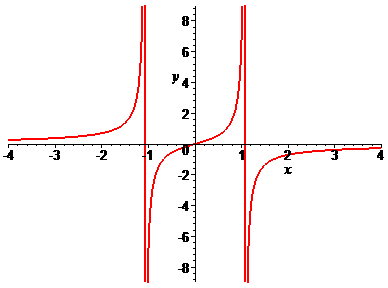
Построить график функции 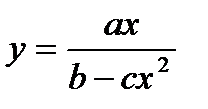 на оптимальном промежутке.
на оптимальном промежутке.
> restart;
> plot([7*x/(8-7*x^2)],x=-4..4,y=-9..9,labels=[x,y],labelfont=[TIMES,ITALIC,12],thickness=2);
Контрольные вопросы.
Как называется пакет дополнительных графических команд?
Пакет дополнительных графических команд называется plots
С помощью какой команды можно построить график неявной функции?
Для построения графика неявной функции используется команда implicitplot из графического пакета plots: implicitplot(F(x,y)=0, x=x1..x2, y=y1..y2).
Лабораторная работа №3
"Построение графиков"
Преподаватель: Выборнова Е. И.
Выполнил работу: Певцова В. Ю.
а=7, b=8, с = 7
Группа: Э-08
Смоленск 2010 г.
Лабораторная работа №3
Выполнил студент Певцова Виктория Юрьевна
Файл с заданиями сохранен по именем Певцова_3
Контрольные задания
Задание 1
Построить на отдельных рисунках графики функций Бесселя первого рода Jn(x) для различных ее номеров n в интервале –20<x<20. Функции Бесселя вызываются командой BesselJ(n,x), где n – номер функции Бесселя, x – независимая переменная. Построить первые 6 функций Бесселя для n=0,1,2,3,4,5,6. Как они выглядят и чем отличаются друг от друга? Сделать подписи осей курсивом.
> plot(BesselJ(0,x),x=-20..20, labels=[x,Jn], labelfont=[TIMES,ITALIC,12]);

> plot(BesselJ(1,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);

> plot(BesselJ(2,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);

> plot(BesselJ(3,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);

> plot(BesselJ(4,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);

> plot(BesselJ(5,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);

> plot(BesselJ(6,x),x=-20..20, labels=[x,Jn],labelfont=[TIMES,ITALIC,12]);

Задание 2
1. Построить график функции 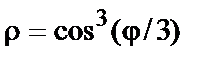 в полярных координатах при 0<j<4p. Используйте цвет линии под названием magenta, установите толщину линии 3.
в полярных координатах при 0<j<4p. Используйте цвет линии под названием magenta, установите толщину линии 3.
> plot(cos(x/3)^3, x=0..4*Pi, coords=polar, color=magenta, thickness=3);

Задание 3
Построить на одном рисунке графики функции  и ее асимптот
и ее асимптот 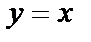 и
и 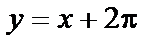 . Установить следующие параметры: цвет основной линии – голубой, асимптот – красный (установлен по умолчанию, поэтому его можно не изменять); толщина основной линии – 3, асимптоты – обычной; масштаб по координатным осям – одинаковый. Сделать надписи: какая функция относится к какой линии. Указание: использовать для преобразования в текст формул команду convert, а для построения графиков и надписей команды textplot и display из пакета plots
. Установить следующие параметры: цвет основной линии – голубой, асимптот – красный (установлен по умолчанию, поэтому его можно не изменять); толщина основной линии – 3, асимптоты – обычной; масштаб по координатным осям – одинаковый. Сделать надписи: какая функция относится к какой линии. Указание: использовать для преобразования в текст формул команду convert, а для построения графиков и надписей команды textplot и display из пакета plots
Задание 4
Построить график функции 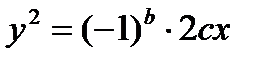 .
.
> with(plots):
implicitplot(y^2=(-1)^8*14*x, x=-20..20, y=-16..16,color=blue, thickness=2, title="Парабола");

Задание 5
Построить график поверхности и определить ее вид 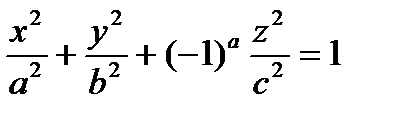 .
.
> with(plots): implicitplot3d((x^2/49)+(y^2/64)+(-1)^7*(z^2/49)=0, x=-5..5, y=-5..5,z=-5...5,scaling=CONSTRAINED,title="Конус");

Задание 6
Построить в одной системе координат графики поверхностей 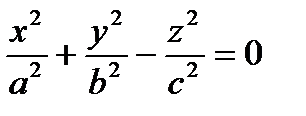 и
и 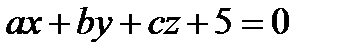 и определить их вид. Пользуясь возможностями Maple, настроить оптимальное изображение.
и определить их вид. Пользуясь возможностями Maple, настроить оптимальное изображение.
> with(plots): implicitplot3d({7*x+8*y+7*z+5=0,x^2/49+y^2/64-z^2/49=0}, x=-5..5, y=-5..5,z=-5...5,scaling=CONSTRAINED,title="Плоскость и конус");

Задание 7
Построить график функции 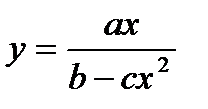 на оптимальном промежутке.
на оптимальном промежутке.
> restart;
> plot([7*x/(8-7*x^2)],x=-4..4,y=-9..9,labels=[x,y],labelfont=[TIMES,ITALIC,12],thickness=2);

Контрольные вопросы.
С помощью каких команд строятся графики на плоскости и в пространстве? Какие аргументы имеют эти команды?
· plot(f(x), x=a..b, y=c..d, parameters), (parameters – параметры управления изображением) используется для построения графиков функции f(x) одной переменной.
· implicitplot(F(x,y)=0, x=x1..x2, y=y1..y2) из графического пакета plots используется для построения графика неявной функции.
· inequals({f1(x,y)>c1,…,fn(x,y)>cn}, x=x1…x2, y=y1..y2, options) из пакета plots используется для построения двумерной области. В команде в фигурных скобках указывается система неравенств, определяющих область, затем размеры координатных осей и параметры.
· plot3d(f(x,y), x=x1…x2, y=y1…y2, options) используя для построения графика поверхности, заданной неявной функции 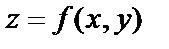 .
.
· plot3d([x(u,v), y(u,v), z(u,v)], u=u1..u2, v=v1..v2) используя для построения поверхности, заданной параметрически (функции перечисляются в квадратных скобках в команде).
· implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2) из пакета plot используя для построения трехмерного графика поверхности, заданной неявно уравнением 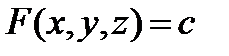 , где указывается уравнение поверхности
, где указывается уравнение поверхности 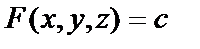 и размеры рисунка по координатным осям.
и размеры рисунка по координатным осям.
· spacecurve из пакета plot используя для построения пространственной кривой, заданной параметрически: 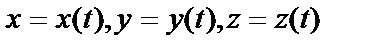 .
.
