Модель управления запасами с фиксированным интервалом времени между заказами
Вторая модель управления запасами— модель с фиксированным интервалом времени между заказами (flxed-order-in- terval model). В модели с фиксированным интервалом времени между заказами, как ясно из названия, заказы делаются в строго определенный моменты времени, которые отстоят друг от друга на равные интервалы, например 1 раз в месяц, 1 раз в неделю, 1 раз в 14 дней и т.п.
Фиксированный интервал времени между заказами должен иметь оптимальный размер. Оптимизация уровня запаса связывается с оптимизацией размера заказа на восполнение запаса. Таким образом, определять оптимальный интервал времени между заказами следует на основе оптимального размера заказа. Оптимальный размер заказа позволяет минимизировать совокупные затраты на содержание и пополнение запаса, а также достичь наилучшего сочетания таких факторов, как используемая площадь складских помещений, издержки на хранение запаса и стоимость заказа.
Методика управления запасами на основе фиксации интервала между заказами заключается в том, что заказы на пополнение запаса делаются в заранее определенный момент через фиксированные интервалы между заказами в размере, который обеспечивает пополнение запаса до максимально желательного уровня.
Все параметры модели рассчитываются таким образом, что при соблюдении исходных данных модель гарантирует бездефицитность обслуживания запасом потребности в условиях определенности (т.е. в условиях постоянного темпа потребления).
Исходными данными для расчета параметров модели с фиксированным интервалом времени между заказами являются следующие показатели:
1) объем потребности в запасе, единиц;
2) интервал времени между заказами, дни;
3) время выполнения заказа, дни;
4) возможная задержка поставки, дни.
Расчетными параметрами модели с фиксированным интервалом времени между заказами являются:
1) максимальный желательный запас, единиц;
2) страховой запас, единиц.
Максимальный желательный запас определяется для отслеживания целесообразной загрузки площадей склада с точки зрения критерия минимизации совокупных затрат.
Страховой (или гарантийный) запас позволяет удовлетворять потребность в запасе на время предполагаемой задержки поставки. При этом под возможной задержкой поставки подразумевается максимальная возможная задержка. Расчет параметров модели управления запасами с фиксированным интервалом времени между заказами приведен в табл. 9.6.
Таблица 9.6 - Расчет параметров модели управления запасами с фиксированным интервалом времени между заказами
| Nen/n | Показатель | Порядок расчета |
| Объем потребности, единиц | — | |
| Интервал времени между заказами, дни | — | |
| Время выполнения заказа, дни | — | |
| Возможная задержка поставки, дни | — | |
| Ожидаемое дневное потребление, единиц/день | [1] / [число рабочих дней] | |
| Ожидаемое потребление за время поставки, единиц | [3] * [5] | |
| Максимальное потребление за время выполнения заказа, единиц | ([3] + [4]) * [5] | |
| Страховой запас, единиц | [5] * [4] | |
| Максимальный желательный запас, единиц | [8] + [2] * [5] |
Пример 9.2. Расчет параметров модели с фиксированным интервалом времени между заказами
Пример расчета основных параметров модели управления запасами с фиксированным интервалом времени между заказами по данным, использованным для расчета модели с фиксированным размером заказа (см. табл. 9.2), приведен в табл. 9.7.
Таблица 9.7
Пример расчета параметров модели управления запасами с фиксированным интервалом времени между заказами
| № п/п | Показатель | Значение |
| Объем потребности, единиц | ||
| Интервал между заказами, дни | ||
| Время выполнения заказа, дни | ||
| Возможная задержка поставки, дни | ||
| Ожидаемое дневное потребление, единиц/день | ||
| Ожидаемое потребление за время выполнения заказа, единиц | ||
| Максимальное потребление за время выполнения заказа, единиц | ||
| Страховой запас, единиц | ||
| Максимальный желательный запас, единиц |
Расчет движения запаса при основных параметрах табл. 9.7 на примере 40 дней приведен в табл. 9.8.
Таблица 9.8
Расчет уровней запаса без задержек поставок при основных параметрах табл. 9.7
| Дни | Запас | Расход | Приход | Размер заказа | ||
| День 1 | ||||||
| День 2 | ||||||
| День 3 | ||||||
| День 4 | ||||||
| День 5 | ||||||
| День 6 | ||||||
| День 7 | ||||||
| День 8 | ||||||
| День 9 | ||||||
| День 10 | ||||||
| День 11 | ||||||
| День 12 | ||||||
| День 13 | ||||||
| День 14 | ||||||
| День 15 | ||||||
| День 16 | ||||||
| День 17 | ||||||
| День 18 | ||||||
| День 19 | ||||||
| День 20 | ||||||
| День 21 | ||||||
| День 22 | ||||||
| День 23 | ||||||
| День 24 | ||||||
| День 25 | ||||||
| День 26 | ||||||
| День 27 | ||||||
| День 28 | ||||||
| День 29 | ||||||
| День 30 | ||||||
| День 31 | ||||||
| День 32 | ||||||
| День 33 | ||||||
| День 34 | ||||||
| День 35 | ||||||
| День 36 | ||||||
| День 37 | ||||||
| День 38 | ||||||
Предположим, что первый заказ делается в первый день. Тогда размер заказа определяется следующим образом: Qx = 40 — 40 + 16 = 16 единиц.
Поставка выданного заказа придет на 5-й день (через 4 дня, см. позицию 3 табл. 9.7). Следующий заказ должен быть выполнен через 9 дней, т.е. на 10-й день, в размере Q2 = 40 — 20 + 16 = 36 единиц.
Без задержек второй заказ придет на 14-й день и т.д. Иллюстрация движения запаса при отсутствии задержек поставок в модели с фиксированным интервалом времени между заказами приводится на рис. 9.7.
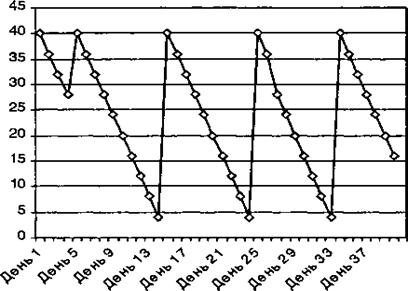
Рис. 9.7. Иллюстрация движения запаса при отсутствии задержек поставки по параметрам табл. 9.7
3.2.3. Модель управления запасами с установленной периодичностью пополнения запаса до постоянного уровня
Основные модели управления запасами можно успешно использовать в условиях относительно стабильного потребления запаса. Между тем довольно часто потребность в запасе имеет колебания сезонного или общего характера. Обеспечение бесперебойного снабжения потребителя в таких условиях требует доработки основных моделей. Одним из результатов проектирования новых моделей, предназначенных для управления запасами при наличии колебаний потребности, является модель с установленной периодичностью пополнения запаса до постоянного уровня. Эта модель предполагает, что дефицит запаса недопустим. Следовательно, модель ориентирована на ситуацию, когда затраты на содержание запаса ниже издержек в результате дефицита, что приводит к необходимости накапливать достаточно большой объем запаса.
В модели с установленной периодичность пополнения запаса до постоянного уровня заказы производятся в установленные моменты времени (как в модели с фиксированным интервалом времени между заказами) и при снижении запаса до порогового уровня (как в модели с фиксированным размером заказа). Таким образом, рассматриваемая модель включает элемент модели с фиксированным интервалом времени между заказами (установленная периодичность выдачи заказа на пополнения запаса) и элемент модели с фиксированным размером заказа (отслеживание порогового уровня запаса). Совместное использование этих элементов позволяет предохранить логистическую систему от дефицитного состояния без излишнего завышения объема запаса.
Отличительную особенность модели с установленной периодичностью пополнения запаса до установленного уровня состоит в том, что заказы делятся на две категории. Плановые заказы производятся через заданные интервалы времени. Возможны дополнительные или внеочередные заказы, если запас на складе снижается до порогового уровня.
Расчет параметров этой модели приведен в табл. 9.11. По составу и расчету параметров модель с установленной периодичностью пополнения запаса до постоянного уровня схожа как с моделью управления запасами с фиксированным размером заказа, так и с моделью управления запасами с фиксированным интервалом времени между заказами (см. табл. 9.1 и 9.6).
Таблица 9.11- Расчет параметров модели управления запасами с установленной периодичностью пополнения запаса до постоянного уровня
| № п/п | Показатель | Порядок расчета |
| Объем потребности, единиц | — | |
| Интервал времени между заказами, дни | — | |
| Время выполнения заказа, дни | — | |
| Возможная задержка поставки, дни | — | |
| Ожидаемое дневное потребление, единиц/ день | [1] / [Количество рабочих дней] | |
| Ожидаемое потребление за время поставки, единиц | [3] * [5] | |
| Максимальное потребление за время выполнения заказа, единиц | ([3] + [4]) * [5] | |
| Страховой запас, единиц | [5] * [4] | |
| Пороговый уровень запаса, единиц | — | |
| Максимальный желательный запас, единиц | [9] + [2] * [5] |
Исходные данные для расчета параметров модели с установленной периодичностью пополнения запаса до постоянного уровня совпадают с моделью управления запасами с фиксированным интервалом времени между заказами. Такими показателями являются:
1) объем потребности в запасе, единиц;
2) интервал времени между заказами, дни;
3) время выполнения заказа, дни;
4) возможная задержка поставки, дни.
Расчетные параметры модели с установленной периодичностью пополнения запаса до постоянного уровня совпадают с расчетными параметрами модели с фиксированным размером заказа. К ним относятся:
1) максимальный желательный запас, единиц;
2) пороговый уровень запаса, единиц;
3) страховой запас, единиц.
Для исходных данных, использованных в модели управления запасами с фиксированным размером заказа (см. табл. 9.2) и в модели с фиксированным интервалом времени между заказами (см. табл. 9.7), проведем расчет параметров модели с установленной периодичностью пополнения запаса до постоянного уровня (табл. 9.12).
Таблица 9.12 - Пример расчета параметров модели с установленной периодичностью пополнения запаса до постоянного уровня
| № п/п | Показатель | Значение |
| Объем потребности, единиц | ||
| Интервал между заказами, дни | ||
| Время выполнения заказа, дни | ||
| Возможная задержка поставки, дни | ||
| Ожидаемое дневное потребление, единиц/день | ||
| Ожидаемое потребление за время выполнения заказа, единиц | ||
| Максимальное потребление за время выполнения заказа, единиц | ||
| Страховой запас, единиц | ||
| Пороговый уровень запаса, единиц | ||
| Максимальный желательный запас, единиц |
Иллюстрация движения запаса на примере изменения потребности при изучении модели с фиксированным размером заказа (см. табл. 9.5) и модели с фиксированным интервалом времени между заказами (см. табл. 9.10) приведена в табл. 9.13.
Таблица 9.13 - Расчет уровней запаса при колебании потребности а запасе и наличии задержек поставок при основных параметрах табл. 9.12
| Дни | Запас | Расход | Приход | Размер заказа | |
| День 1 | |||||
| День 2 | |||||
| День 3 | |||||
| День 4 | |||||
| День 5 | |||||
| День 6 | |||||
| День 7 | |||||
| День 8 | |||||
| День 9 | |||||
| День 10 | |||||
| День 11 | |||||
| День 12 | |||||
| День 13 | |||||
| День 14 | |||||
| День 15 | |||||
| День 16 | |||||
| День 17 | |||||
| День 18 | |||||
| День 19 | |||||
| День 20 | |||||
| День 21 | |||||
| День 22 | |||||
| День 23 | |||||
| День 24 | |||||
| День 25 | |||||
| День 26 | |||||
| День 27 | |||||
| День 28 | |||||
| День 29 | |||||
| День 30 | |||||
| День 31 | |||||
| День 32 | |||||
| День 33 | |||||
| День 34 | |||||
| День 35 | |||||
| День 36 | |||||
| День 37 | |||||
| День 38 | |||||
| День 39 | |||||
| День 40 | -5 | ||||
| День 41 | |||||
| День 42 | |||||
| День 43 | |||||
| День 44 | |||||
| День 45 | |||||
| День 46 | |||||
| День 47 | |||||
| День 48 | |||||
| День 49 | |||||
| День 50 | |||||
Плановые заказы выполняются в 10, 20, 30,40 и 50-й дни. Расчет размера заказа. Так, в 1-й день размер заказа рассчитан следующим образом: Qx = 44 — 44 + 16 = 16.
На 10-й день размер заказа делается в объеме
Q2 = 44 — 24 + 16 = 36 и т.д.
Соответственно, плановые заказы приходят без задержки в 14, 24, 34, 44-й и т.д. дни.
Внеочередные заказы делаются при снижении запаса до порогового уровня. Расчет порогового уровня запаса в данном случае выполнен по классической формуле: ПУ = 4+ 16 = 20.
Внеочередные заказы в рассматриваемом примере должны быть сделаны в 11-й день (уровень запаса равен 20), в 23-й день (уровень запаса равен 15), в 37-й день (уровень запаса равен 18). Предполагается, что все внеочередные заказы пришли в срок.
В результате, как видно из рис. 9.10, результат работы модели с установленной периодичностью пополнения запаса до постоянного уровня значительно лучше, чем моделей с фиксированным размером заказа (см. рис. 9.5) и с фиксированным интервалом времени между заказами (см. рис. 9.8). Незначительный дефицит в 5 единиц появляется только в 40-й день и только в течение одного дня. Он покрывается внеочередной поставкой, организованной в 37-й день.
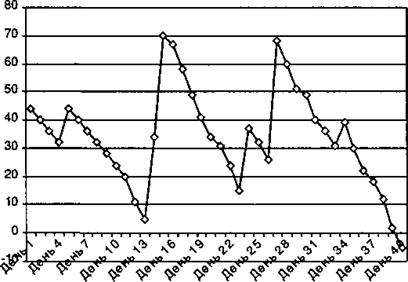
Рис. 9.11. Иллюстрация движения запаса при колебании потребности в запасе и наличии задержек поставки по параметрам табл. 9.12
Таким образом, модель с установленной периодичностью пополнения запаса до постоянного уровня позволяет удовлетворять изменяющиеся потребности в запасе с минимальным уровнем дефицита.
