Структурные схемы синтезированной системы
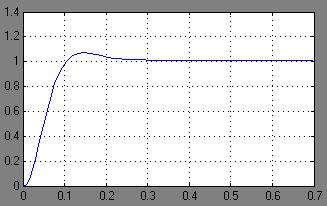
В Simulink построим структурные схемы синтезированной и получим по ним передаточные функции. Переходная характеристика по задающему воздействию.
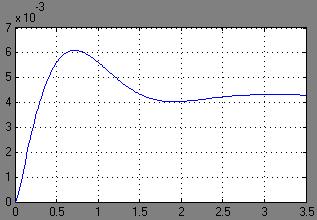
Переходная характеристика по возмущающему воздействию.
Анализ синтезированной системы
Определим показатели качества синтезированной системы и сравним их с требуемыми. Переходная характеристика системы на задающее воздействие.
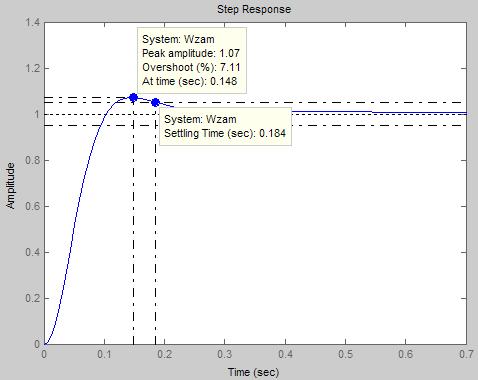
Время переходного процесса: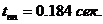 
Перерегулирование: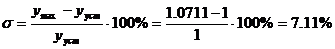 
Передаточная функция разомкнутой синтезированной системы:
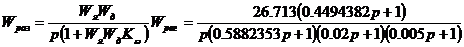
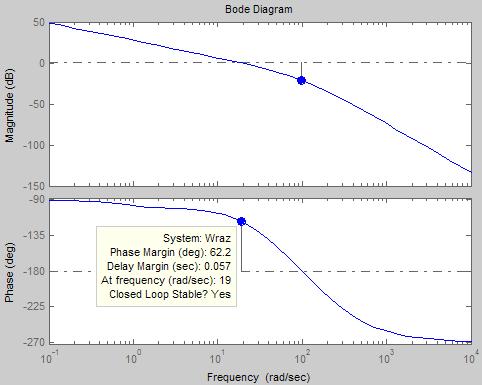
Запас устойчивости по фазе: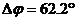 
.
Аналитическое конструирование регулятора
Проведем аналитическое конструирование регулятора на основе метода динамического программирования. Модель пространств и состояний:
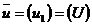
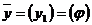
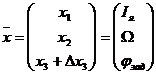
Пусть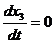 
. Определим матрицы:
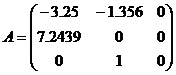
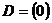
Определим матрицу C с помощью функции care в MATLAB.
>> A = [-3.25 -1.356 0; 7.2439 0 0; 0 1 0]
A =
-3.25000000000000 -1.35600000000000 0
7.24390000000000 0 0
0 1.00000000000000 0
>> B = [3.25; 0; 0]
B =
3.25000000000000
>> Q = [1 0 0; 0 1 0; 0 0 1]
Q =
1 0 0
0 1 0
0 0 1
>> care(A, B, Q)
ans =
0.45996310614966 0.29158510528578 0.30769230769231
0.29158510528578 0.37000714512288 0.34441117284700
0.30769230769231 0.34441117284700 1.36488236140955
>> C = -ans*B
C =
-1.49488009498639
-0.94765159217878
-1.00000000000000
>> transpose(C)
ans =
-1.49488009498639 -0.94765159217878 -1.00000000000000
Матрица C будет иметь следующий вид: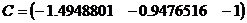 
.
Построим в Simulink схему синтезированного привода и получим реакцию системы на входные воздействия.
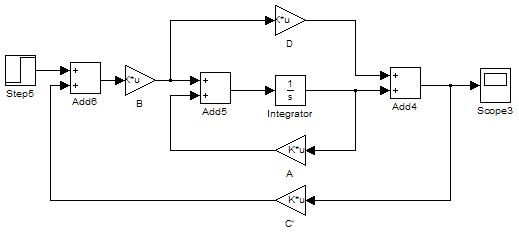
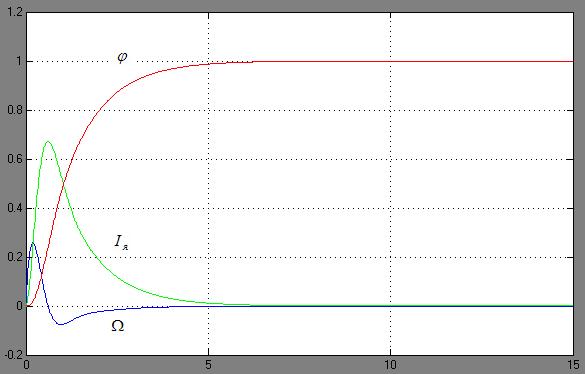
Определим матрицу C с помощью функции lyap в MATLAB.
>> A = [-3.25 -1.356 0; 7.2439 0 0; 0 1 0]
A =
-3.25000000000000 -1.35600000000000 0
7.24390000000000 0 0
0 1.00000000000000 0
>> Q = [1 0 0; 0 1 0; 0 0 1]
Q =
1 0 0
0 1 0
0 0 1
>> lyap(A, Q)
??? Solution does not exist or is not unique
Таким образом, решение уравнения Ляпунова не существует или не является единственным.
Вывод
В данной курсовой работе я приобрел практический навык и закрепил теоретические знания по анализу и синтезу систем автоматического управления.
В данной работе были проанализированы статические и динамические характеристики системы управления и проведен синтез корректирующих цепей для получения требуемых показателей качества функционирования САУ. При выполнении курсовой работы были решены следующие задачи:
· Составлена структурная схема исходной системы по заданной функциональной схеме;
· Проведен анализ динамических и статических свойств исходной САУ;
· Синтезирована система, отвечающая предъявляемым требованиям к ней.
· Проведен синтез регулятора по уравнению Рикатти.
В результате получилась синтезированная система, которая удовлетворяет требуемым показателям качества системы.
Время переходного процесса: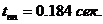
Перерегулирование: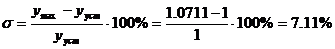
Запас устойчивости по фазе: .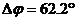
Список использованной литературы
1. Александров А.Г. «Оптимальные и адаптивные системы». М.: Высш. шк., 1989.
2. MATLAB 5 для студентов, Медведев В.С., Потемкин В.Г/ Под общ. ред. к.т.н. В.Г. Потемкина. – М.: ДИАЛОГ-МИФИ, 1999.
3. Потемкин В.Г., Рудаков П.И. «Система MATLAB 5 для студентов». – 2-е изд. испр. и дополн. – М.: ДИАЛОГ-МИФИ, 1999.
4. Ахмадеев И.А. «Теория автоматического управления. Использование системы MATLAB для исследования систем автоматического управления. Лабораторный практикум».
5. Ахмадеев И.А. «Теория автоматического управления. Практикум. Часть 1».