Полная аэродинамическая сила и ее проекции

Полная аэродинамическая сила и ее проекции

При расчете основных летно-технических характеристик самолета, а также его устойчивости и управляемости необходимо знать силы и моменты, действующие на самолет.

Аэродинамические силы, действующие на поверхность самолета (давление и трение), можно привести к главному вектору аэродинамических сил , приложенному в центре давления (рис. 1), и паре сил, момент которых равен главному моменту аэродинамических сил относительно центра масс летательного аппарата.

Рис. 1. Полная аэродинамическая сила и ее проекции в двумерном (плоском) случае

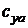Аэродинамическую силу обычно задают проекциями на оси скоростной системы координат (ГОСТ 20058-80). При этом проекцию на ось , взятую с обратным знаком, называют силой лобового сопротивления , проекцию на ось - аэродинамической подъемной силой , проекцию на ось - аэродинамической боковой силой . Эти силы могут быть выражены через безразмерные коэффициенты лобового сопротивления , подъемной силы и боковой силы , соответственно:

; ; ,

где - скоростной напор, Н/м²; - воздушная скорость, м/с; r - массовая плотность воздуха, кг/м³; S - площадь крыла самолета, м². К основным аэродинамическим характеристикам относят также аэродинамическое качество

.

Аэродинамические характеристики крыла , , 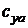зависят от геометри­ческих параметров профиля и крыла, ориентации крыла в потоке (угла атаки a и скольжения b), параметров подобия (чисел Рейнольдса Re и Маха ),высоты полета H, а также от других параметров. Числа Маха и Рейнольдса являются безразмерными величинами и определяются выражениями

, , (2.12)

где a – скорость звука, n - кинематический коэффициент вязкости воздуха в м²/с, – характерный размер (как правило полагают , где – средняя аэродинамическая хорда крыла).Для определения аэродинамических характеристик самолета иногда исполь­зуются более простые, приближенные методы. Самолет рассматривается как совокупность отдельных частей: крыла, фюзеляжа, оперения, гондол двигателей и т.д. Определяются силы и моменты, действующие на каждую из отдельных частей. При этом используются известные результаты аналитических, численных и экспериментальных исследований. Силы и моменты, действующие на самолет, находятся как сумма соответствующих сил и моментов, действующих на каждую из его частей, с учетом их взаимного влияния.

Согласно предлагаемой методике, расчет аэродинамических харак­теристик крыла производится, если заданы некоторые геометрические и аэродинамические характеристики профиля крыла.

Выбор профиля крыла

Основные геометрические характеристики профиля задаются следующими параметрами. Хордой профиля называется отрезок прямой, соединенной две наиболее удаленные точки профиля. Хорда делит профиль на две части: верхнюю и нижнюю. Наибольший перпендикулярный хорде отрезок, заключенный между верхним и нижним обводами профиля, называется толщиной профиля c (рис. 2). Линия, соединяющая середины отрезков, перпендикулярных хорде и заключенных между верхним и нижним обводами профиля, называется средней линией. Наибольший перпендикулярный хорде отрезок, заключенный между хордой и средней линией профиля, называется кривизной профиля f. Если , то профиль называется симметричным.

Рис. 2. Профиль крыла

b - хорда профиля; c - толщина профиля; f - кривизна профиля; - координата максимальной толщины; - координата максимальной кривизны

Толщину c и кривизну профиля f, а также координаты и , как правило измеряют в относительных единицах , , , или в процентах , , , .

Выбор профиля крыла связан с удовлетворением различных требований, предъявляемых к самолету (обеспечение требуемой дальности полета, высокой топливной эффективности,крейсерской скорости , обеспечение безопасных условий взлета и посадки и др.). Так, для легких самолетов с упрощенной механизацией крыла следует обращать особое внимание на обеспечение максимального значения коэффициента подъемной силы, особенно на режиме взлета и посадки. Как правило, такие самолеты имеют крыло с большим значением относительной толщины профиля 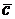% = 12 ¸ 15%.

Для дальних самолетов с высокой дозвуковой скоростью полета, у которых увеличение 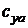на взлетно-посадочных режимах достигается благодаря механизации крыла, упор делается на достижение лучших характеристик на крейсерском режиме, в частности, на обеспечение режимов [1,2].

Для нескоростных самолетов выбор профилей производится из серии стандартных (обычных) профилей NACA или ЦАГИ, которые при необходи­мости могут быть модифицированы на этапе эскизного проектирования самолета.

Так, профили NACA с четырехзначными обозначениями могут быть использованы на легких тренировочных самолетах, а именно для концевых сечений крыла и хвостового оперения. Например, профили NACA2412 (относительная толщина 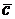% = 12%, координата максимальной толщины % = 30%, относительная кривизна % = 2%, координата максимальной кривизны % = 40%) и NACA4412 ( 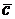% = 12%, % = 30%, % = 4%, % = 40%) имеют достаточно высокое значение 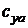и плавные срывные характеристики в районе критического угла атаки .

Пятизначные профили NACA (серии 230) обладают наибольшей подъемной силой из всех стандартных серий, но их срывные характеристики менее благоприятны.

Профили NACA с шестизначным обозначением ("ламинарные") имеют низкое профильное сопротивление в узком диапазоне значений коэф­фициента 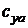. Эти профили очень чувствительны к шероховатости поверхности, загрязнениям, наростам [3].

Классические (обычные) профили, используемые на самолетах с малы­ми дозвуковыми скоростями, отличаются достаточно большими местными возмущениями (разряжениями) на верхней поверхности и, соответственно, небольшими значениями критического числа Маха 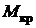. Критическое число Маха является важным параметром, определяющим величину лобового сопротивления самолета (при > 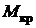на поверхности летательного аппарата появляются области местных сверхзвуковых течений и дополнительное волновое сопротивление).

Активный поиск путей повышения крейсерской скорости полета (без увеличения сопротивления самолета) привел к необходимости изыскать спо­собы дальнейшего повышения 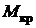по сравнению с классическими скорост­ными профилями. Таким способом повышения 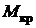является уменьшение кривизны верхней поверхности, что приводит к снижению возмущений на значительной части верхней поверхности. При малой искривленности верхней поверхности сверхкритического профиля уменьшается доля создаваемой им подъемной силы. Для компенсации этого явления производится подрезка хвостового участка профиля путем плавного изгиба его вниз (эффект "закрылка"). В связи с этим, средняя линия суперкритических профилей имеет харак­терный S - образный вид, с отгибом вниз хвостового участка. Для суперкритических профилей, как правило, характерно наличие отрицательной кривизны в носовой части профиля. В частности, на авиасалоне МАКС 2007 в экспозиции ОАО ²Туполев² был представлен макет самолета ТУ-204-100СМ с усеченным крылом, что позволяет получить представление о геометрических характеристиках профиля в корневой части крыла. Из представленного ниже фото (рис. 3.) видно наличие у профиля ²брюшка² и достаточно плоской верхней части, характерных для суперкритических профилей. Сверх­критические профили по сравнению с обычными скоростными профилями позволяют повысить 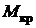примерно на = 0,05 ¸ 0,12 или увеличить тол­щину на % = 2,5 ¸ 5%. Применение утолщенных профилей позволяет увели­чить удлинение lкрыла на = 2,5 ¸ 3 или уменьшить угол стреловид­ности c крыла примерно на = 5 ¸ 10° при сохранении значения .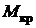

Рис. 3. Профиль крыла самолета ТУ-204-100СМ

Использование сверхкритических профилей в компоновке стреловид­ных крыльев является одним из основных направлений совершенствования аэродинамики современных транспортных и пассажирских самолетов [1].

Следует отметить, что при несомненном преимуществе сверхкритичес­ких профилей, по сравнению с обычными, некоторыми недостатками их яв­ляются повышение значения коэффициента момента на пикирование и тонкая хвостовая часть профиля.

Исходные данные для расчета

Исходные данные для расчета определяются следующими характе­ристиками профиля и крыла. Аэродинамические характеристики обычных профилей можно найти в работах [4, 6, 7, 8]. Некоторые сведения по аэродинамическому проектированию крыльев современных дозвуковых самолетов изложены в работах [1, 3, 9]. Метод расчета аэродинамических характеристик сверхзву­ковых самолетов можно найти в учебных пособиях [10, 11].

Переход от аэродинамических характеристик крыла к характеристикам самолета можно выполнить, используя методику [1, 3, 11].

1. Параметры профиля задаются следующими величинами (при числе Маха = 0,2 и некотором значении числа Рейнольдса Re_¥ = Re₁):

- тип профиля (обычный, суперкритический);

- относительная кривизна или % ;

- относительная толщина или %;

- угол нулевой подъемной силы , град;

- критический угол атаки , град;

- максимальный коэффициент подъемной силы ;

- минимальный коэффициент лобового сопротивления ;

- производная коэффициента подъемной силы по углу атаки .

Например, для профиля NACA 4412 имеем 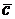% = 12%; % =30%; % = 4%; ; ; =5,5 1/рад; =1,52; = 0,0068; =13°.

2. Параметры крыла:

- корневая хорда крыла , м;

- концевая хорда крыла , м;

- удлинение крыла ;

- сужение крыла ;

- угол крутки концевого сечения крыла 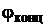, град;

- угол стреловидности , град;

- размах крыла , м.

Параметры потока задаются на режиме крейсерского полета величинами:

- число Маха М_крейс;

- скорость звука a, м/с;

- коэффициент кинематической вязкости n, м²/с;

- высота полета Н.

3. С помощью формулы (по заданному углу ) определяются углы стреловидности по линии 0,5 хорды (m = 0,5) и по линии максимальных толщин (m = = (%)/100). Расчет этих углов производится после определения угла

.

5. Задаются числа Маха, например,

= 0,2; 0,85.

6. Вычисляются значения чисел Рейнольдса

,

где , [м];

, 1/м; H - высота полета в км. Формула справедлива при км.

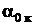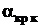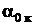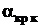7. Расчет зависимостей и производится для серии заданных углов атаки a в диапазоне , град, где - угол нулевой подъемной силы крыла, - критический угол атаки крыла. Величины и - определяются в процессе расчета (см. п.3.2 и п.3.3).

Шаг по углу атаки определяется выражением

,

где - число расчетных точек. Таким образом, расчет производится при следующих значениях угла атаки

- угол атаки в градусах .

При расчетах без использования компьютера минимальное количество углов атаки, для которых задается расчет, равно трем: , , (определение угла в п.3.5).

Подъемной силы крыла

Коэффициент аэродинамической подъемной силы крыла 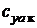зави­сит от геометрических и аэродинамических характеристик профиля, геометрических параметров крыла, угла атаки α, критериев подобия Re и M. Рассмотрим методику определения 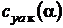для изолированного крыла с учетом вышеперечисленных параметров.

Зависимость коэффициента подъемной силы 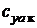от угла атаки 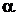в общем случае можно поде­лить на две области. Первая область 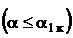характеризуется безотрыв­ным обтеканием и линейной зависимостью 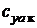от (коэффициент подъемной силы прямо пропорционален углу атаки). Вторая область характеризуется тем, что по мере увеличения угла атаки (при 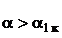) и расширении области отрыва потока (это так называемый диффузорный отрыв потока) рост коэффициента подъемной силы замедляется и достигает максимума при критическом угле атаки крыла, а затем уменьшается. Здесь 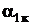- угол атаки крыла, при котором начинается интенсивный срыв потока и который называется допустимым углом атаки или углом тряски. Угол атаки, соответствующий 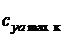, называется критическим углом атаки 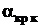. Отметим, что в данной работе угол 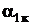определяется из условия гладкого сопряжения линейной и нелинейной областей кривой 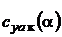. Характер зависимости нелинейной части от угла атаки для упрощения выбран в виде квадратичного полинома, что не всегда соответствует действительности. В следствие этого, значения угла 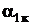могут оказаться заниженными, особенно для больших чисел Маха.

3.1. Расчет производной коэффициента подъемной силы по углу атаки 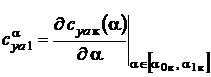(на линейном участке) для числа Рейнольдса 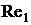производится по формулам [3]:

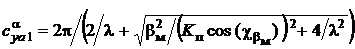, (1)

где

, , .

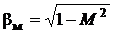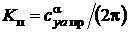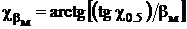3.2. Расчет нулевого угла атаки крыла 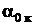.С учетом крутки крыла угол 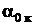определяется из следующих выражений [4]:

,

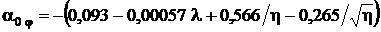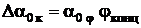, (2)

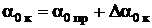. (3)

Здесь 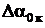- слагаемое, зависящее от крутки крыла, которое определено для случая равномерной крутки по размаху крыла. С точки зрения получения максимального аэродинамического качества K рекомендуется угол крутки концевого сечения взять 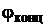» - 4° (если 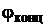< 0, то аэродинамический угол атаки концевого сечения меньше корневого).

3.3. Расчет критического угла атаки крыла :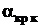

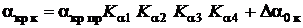, (4)

где

;

;

;

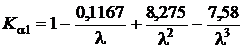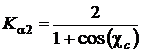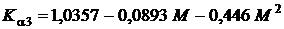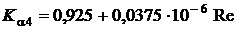, если ;

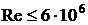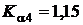при .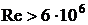

3.4. Расчет максимального значения коэффициента подъемной силы 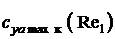крыла (для числа Рейнольдса Re₁) с учетом сжимаемости можно приближенно определить по формулам:

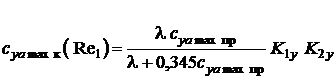, (5)

где

,

.

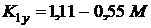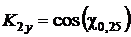3.5. Расчет угла окончания линейного участка 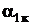из условия гладкого сопряжения линейного и нелинейного участка:

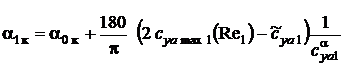, град, (6)

где

.

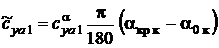3.6. Расчет коэффициента подъемной силы 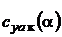(на линейном и нелинейном участках).

Предварительно определяем коэффициент 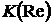, учитывающий влияние числа Рейнольдса на коэффициент подъемной силы [3, 5]. Расчет производится после определения параметра t с помощью выражения

,

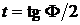где F - угол схода (угол между верхней и нижней поверхностями) хвостовой кромки профиля. Приближенное значение F можно вычислить по формуле

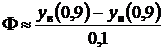в радианах.

Здесь 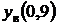и 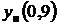- координаты верхней и нижней поверхностей профиля при 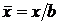= 0,9.

Для четырех – и пятизначных профилей NACA можно использовать более простую формулу:

.

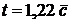Коэффициент, 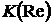можно рассчитать по формуле

,

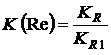где ,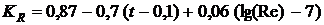

.

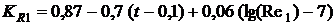Здесь принято, что переход ламинарного к турбулентному режиму течения в пограничном слое происходит около передней кромки [3]. Формулу для 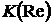можно использовать в диапазоне чисел Рейнольдса 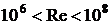. При ориентировочных расчетах можно полагать .

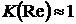Коэффициент подъемной силы крыла на линейном участке 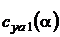(для числа Рейнольдса Re₁) определяется выражением

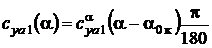, (7)

где углы 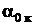, a измеряются в градусах.

Определим теперь 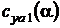на нелинейном участке при 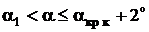(для числа Рейнольдса Re₁). При диффузорном отрыве потока можно принять [5]:

,

,

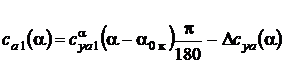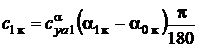где .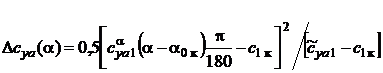

С учетом влияния числа Рейнольдса окончательно получим выражение для зависимости коэффициента подъемной силы 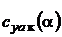крыла для данного угла атаки a

;

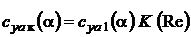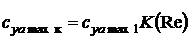
и выражение для производной коэффициента подъемной силы

.

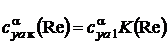Полная аэродинамическая сила и ее проекции

При расчете основных летно-технических характеристик самолета, а также его устойчивости и управляемости необходимо знать силы и моменты, действующие на самолет.

Аэродинамические силы, действующие на поверхность самолета (давление и трение), можно привести к главному вектору аэродинамических сил , приложенному в центре давления (рис. 1), и паре сил, момент которых равен главному моменту аэродинамических сил относительно центра масс летательного аппарата.

Рис. 1. Полная аэродинамическая сила и ее проекции в двумерном (плоском) случае

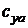Аэродинамическую силу обычно задают проекциями на оси скоростной системы координат (ГОСТ 20058-80). При этом проекцию на ось , взятую с обратным знаком, называют силой лобового сопротивления , проекцию на ось - аэродинамической подъемной силой , проекцию на ось - аэродинамической боковой силой . Эти силы могут быть выражены через безразмерные коэффициенты лобового сопротивления , подъемной силы и боковой силы , соответственно:

; ; ,

где - скоростной напор, Н/м²; - воздушная скорость, м/с; r - массовая плотность воздуха, кг/м³; S - площадь крыла самолета, м². К основным аэродинамическим характеристикам относят также аэродинамическое качество

.

Аэродинамические характеристики крыла , , 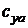зависят от геометри­ческих параметров профиля и крыла, ориентации крыла в потоке (угла атаки a и скольжения b), параметров подобия (чисел Рейнольдса Re и Маха ),высоты полета H, а также от других параметров. Числа Маха и Рейнольдса являются безразмерными величинами и определяются выражениями

, , (2.12)

где a – скорость звука, n - кинематический коэффициент вязкости воздуха в м²/с, – характерный размер (как правило полагают , где – средняя аэродинамическая хорда крыла).Для определения аэродинамических характеристик самолета иногда исполь­зуются более простые, приближенные методы. Самолет рассматривается как совокупность отдельных частей: крыла, фюзеляжа, оперения, гондол двигателей и т.д. Определяются силы и моменты, действующие на каждую из отдельных частей. При этом используются известные результаты аналитических, численных и экспериментальных исследований. Силы и моменты, действующие на самолет, находятся как сумма соответствующих сил и моментов, действующих на каждую из его частей, с учетом их взаимного влияния.

Согласно предлагаемой методике, расчет аэродинамических харак­теристик крыла производится, если заданы некоторые геометрические и аэродинамические характеристики профиля крыла.

Выбор профиля крыла

Основные геометрические характеристики профиля задаются следующими параметрами. Хордой профиля называется отрезок прямой, соединенной две наиболее удаленные точки профиля. Хорда делит профиль на две части: верхнюю и нижнюю. Наибольший перпендикулярный хорде отрезок, заключенный между верхним и нижним обводами профиля, называется толщиной профиля c (рис. 2). Линия, соединяющая середины отрезков, перпендикулярных хорде и заключенных между верхним и нижним обводами профиля, называется средней линией. Наибольший перпендикулярный хорде отрезок, заключенный между хордой и средней линией профиля, называется кривизной профиля f. Если , то профиль называется симметричным.

Рис. 2. Профиль крыла

b - хорда профиля; c - толщина профиля; f - кривизна профиля; - координата максимальной толщины; - координата максимальной кривизны

Толщину c и кривизну профиля f, а также координаты и , как правило измеряют в относительных единицах , , , или в процентах , , , .

Выбор профиля крыла связан с удовлетворением различных требований, предъявляемых к самолету (обеспечение требуемой дальности полета, высокой топливной эффективности,крейсерской скорости , обеспечение безопасных условий взлета и посадки и др.). Так, для легких самолетов с упрощенной механизацией крыла следует обращать особое внимание на обеспечение максимального значения коэффициента подъемной силы, особенно на режиме взлета и посадки. Как правило, такие самолеты имеют крыло с большим значением относительной толщины профиля 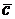% = 12 ¸ 15%.

Для дальних самолетов с высокой дозвуковой скоростью полета, у которых увеличение 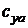на взлетно-посадочных режимах достигается благодаря механизации крыла, упор делается на достижение лучших характеристик на крейсерском режиме, в частности, на обеспечение режимов [1,2].

Для нескоростных самолетов выбор профилей производится из серии стандартных (обычных) профилей NACA или ЦАГИ, которые при необходи­мости могут быть модифицированы на этапе эскизного проектирования самолета.

Так, профили NACA с четырехзначными обозначениями могут быть использованы на легких тренировочных самолетах, а именно для концевых сечений крыла и хвостового оперения. Например, профили NACA2412 (относительная толщина 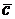% = 12%, координата максимальной толщины % = 30%, относительная кривизна % = 2%, координата максимальной кривизны % = 40%) и NACA4412 ( 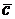% = 12%, % = 30%, % = 4%, % = 40%) имеют достаточно высокое значение 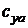и плавные срывные характеристики в районе критического угла атаки .

Пятизначные профили NACA (серии 230) обладают наибольшей подъемной силой из всех стандартных серий, но их срывные характеристики менее благоприятны.

Профили NACA с шестизначным обозначением ("ламинарные") имеют низкое профильное сопротивление в узком диапазоне значений коэф­фициента 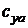. Эти профили очень чувствительны к шероховатости поверхности, загрязнениям, наростам [3].

Классические (обычные) профили, используемые на самолетах с малы­ми дозвуковыми скоростями, отличаются достаточно большими местными возмущениями (разряжениями) на верхней поверхности и, соответственно, небольшими значениями критического числа Маха 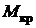. Критическое число Маха является важным параметром, определяющим величину лобового сопротивления самолета (при > 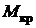на поверхности летательного аппарата появляются области местных сверхзвуковых течений и дополнительное волновое сопротивление).

Активный поиск путей повышения крейсерской скорости полета (без увеличения сопротивления самолета) привел к необходимости изыскать спо­собы дальнейшего повышения 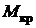по сравнению с классическими скорост­ными профилями. Таким способом повышения 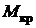является уменьшение кривизны верхней поверхности, что приводит к снижению возмущений на значительной части верхней поверхности. При малой искривленности верхней поверхности сверхкритического профиля уменьшается доля создаваемой им подъемной силы. Для компенсации этого явления производится подрезка хвостового участка профиля путем плавного изгиба его вниз (эффект "закрылка"). В связи с этим, средняя линия суперкритических профилей имеет харак­терный S - образный вид, с отгибом вниз хвостового участка. Для суперкритических профилей, как правило, характерно наличие отрицательной кривизны в носовой части профиля. В частности, на авиасалоне МАКС 2007 в экспозиции ОАО ²Туполев² был представлен макет самолета ТУ-204-100СМ с усеченным крылом, что позволяет получить представление о геометрических характеристиках профиля в корневой части крыла. Из представленного ниже фото (рис. 3.) видно наличие у профиля ²брюшка² и достаточно плоской верхней части, характерных для суперкритических профилей. Сверх­критические профили по сравнению с обычными скоростными профилями позволяют повысить 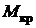примерно на = 0,05 ¸ 0,12 или увеличить тол­щину на % = 2,5 ¸ 5%. Применение утолщенных профилей позволяет увели­чить удлинение lкрыла на = 2,5 ¸ 3 или уменьшить угол стреловид­ности c крыла примерно на = 5 ¸ 10° при сохранении значения .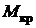

Рис. 3. Пр