Основные способы построения МЦС

1. Один способ уже рассмотрен при доказательстве теоремы о существовании МЦС.

2. Визуальный способ. Иногда сразу удается указать точку плоской фигуры, скорость которой в данный момент времени равна нулю. Например, в случае качения тела по неподвижной поверхности без проскальзывания точка контакта тела с неподвижной поверхностью имеет нулевую скорость и является мгновенным центром скоростей. На рис. 38 точка Р является мгновенным центром скоростей для тела 2.

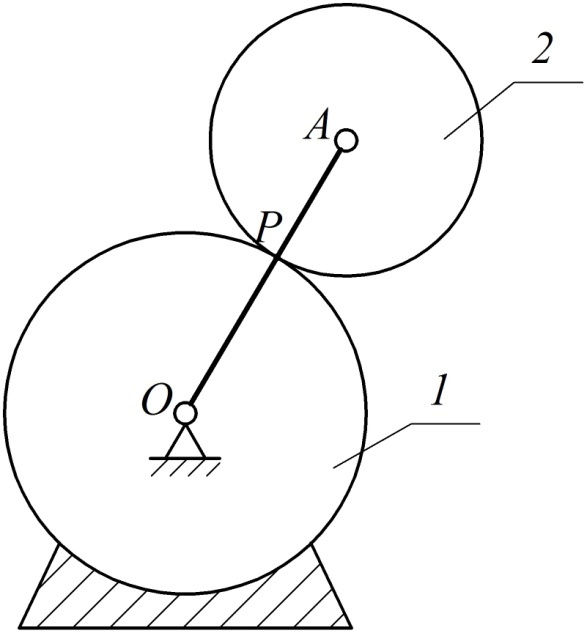
Рис. 38

3. Если известны направления скоростей в двух точках тела, то, как видно из рис. 37, мгновенный центр скоростей найдется как точка пересечения перпендикуляров к скоростям этих точек тела. Этот способ нахождения МЦС чаще всего используется на практике. Здесь следует отметить два частных случая.

3.а. Если точки лежат на общем перпендикуляре к скоростям этих точек, нужно дополнительно знать величины скоростей. В этом случае МЦС найдется как точка пересечения общего перпендикуляра к скоростям и прямой, проведенной через концы векторов скоростей точек, изображенных в выбранном масштабе (см. рис. 39). Этот способ построения следует из пропорциональности скоростей точек тела расстояниям от этих точек до МЦС (см. формулу (49)).

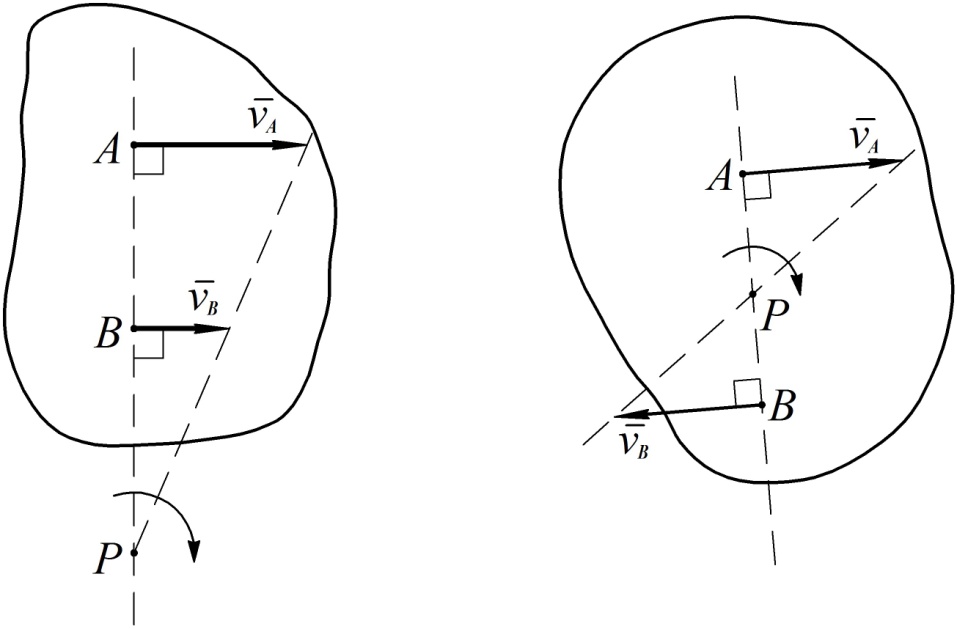
Рис.39

3.б. Если перпендикуляры к скоростям точек тела (случай 3) или общий перпендикуляр к скоростям точек и прямая, проведенная через концы векторов скоростей, (случай 3.а) параллельны, то говорят, что МЦС находится в бесконечности (см. рис. 40).

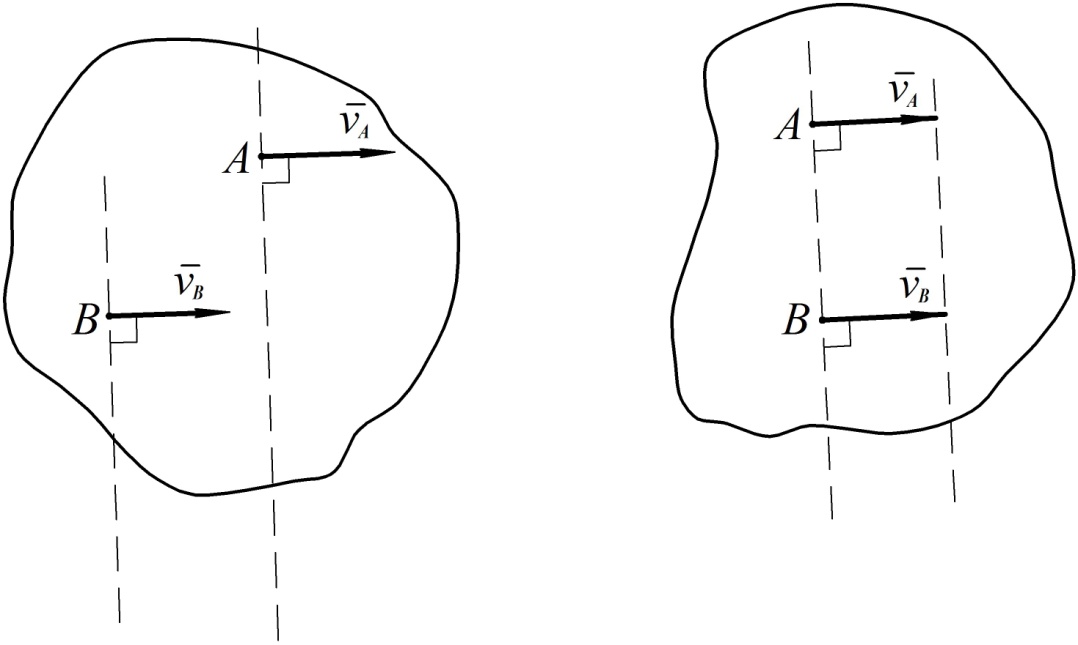
Рис. 40

В этом случае движение тела называют мгновенно-поступательным. При мгновенно-поступательном движении угловая скорость тела равна нулю

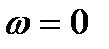
и скорости всех точек тела равны по величине и одинаково направлены

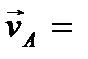
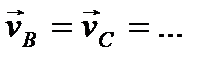
Заметим, что при мгновенно-поступательном движении в отличие от поступательного траектории различных точек тела и их ускорения не будут одинаковыми.

Пример 6

Кривошип ОА длиной ОА=0,2 м вращается вокруг неподвижной оси О с угловой скоростью 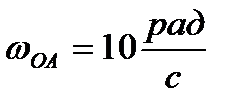. С помощью шатуна АВ кривошип приводит в движение диск радиуса R=0,1м, катящийся по горизонтальной плоскости без проскальзывания. В положении, указанном на рисунке 41 (когда кривошип вертикален, а шатун горизонтален), найти угловую скорость диска и скорости точек C и D.

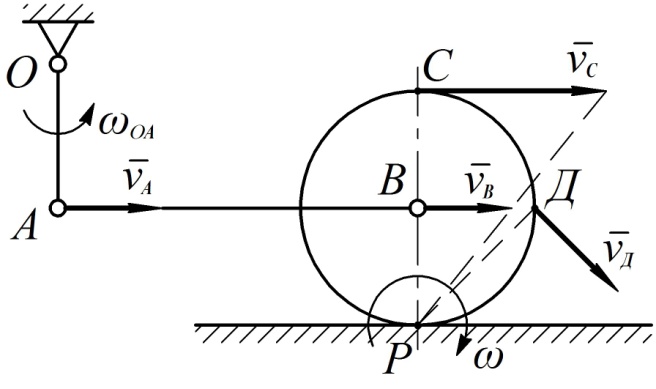
Рис. 41

Решение

Вычислим вначале скорость точки А

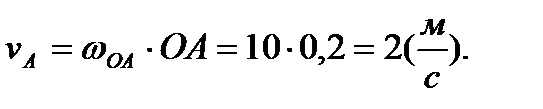
Покажем вектор 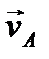на рисунке, направив его перпендикулярно ОА и согласовав по направлению с направлением угловой скорости 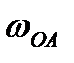. Шатун совершает плоское движение. Построим для шатуна АВ мгновенный центр скоростей. Проведем перпендикуляры к скоростям точек А и В (при этом учтем, что скорость точки В направлена горизонтально, так как траекторией этой точки является горизонтальная прямая). Проведенные перпендикуляры параллельны. Следовательно, мгновенный центр скоростей шатуна находится в бесконечности и скорости точек А и В равны по величине и одинаково

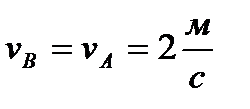
направлены. Покажем вектор 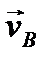на рисунке. Так как диск катится без проскальзывания, то его МЦС находится в точке контакта с опорной поверхностью (точка Р на рисунке). Найдем теперь угловую скорость диска

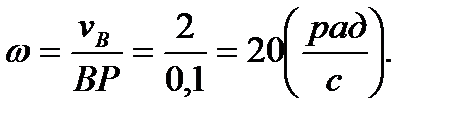
Покажем ее на рисунке, согласовав по направлению со скоростью точки В. Далее легко вычислить величины скоростей точек C и D диска

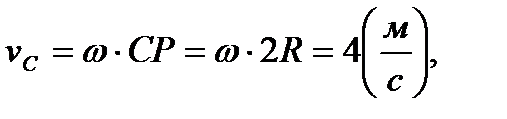
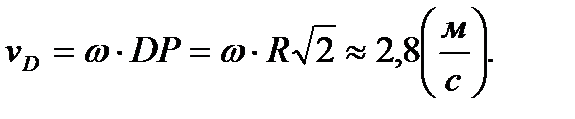
Покажем векторы 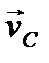и 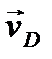на рисунке, направив их перпендикулярно отрезкам СР и DР и согласовав по направлению с ω.