Скорости точек тела при плоском движении

В данном параграфе рассмотрим способы вычисления скоростей точек тела при плоском движении. Эти способы основаны на двух доказываемых ниже теоремах.

Теорема сложения скоростей при плоском движении тела

Скорость любой точки плоской фигуры может быть вычислена как геометрическая сумма скорости полюса и скорости точки при ее относительном вращении вокруг подвижной оси, связанной с полюсом.

Доказательство

Рассмотрим движение точки М плоской фигуры как сложное, связав поступательно перемещающуюся подвижную систему координат с полюсом А (см. рис. 34).

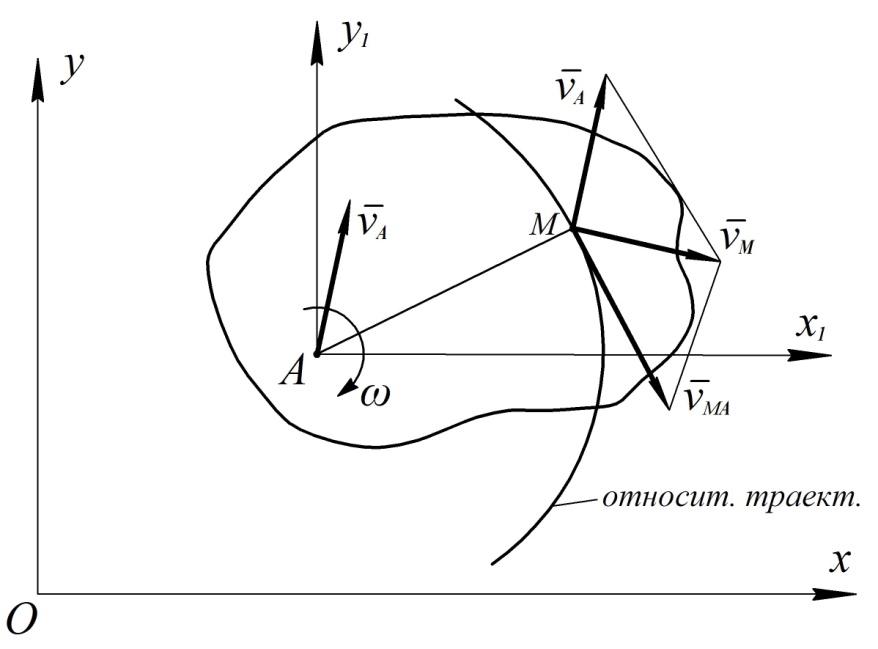
Рис. 34

Тогда по теореме сложения скоростей при сложном движении точки имеем

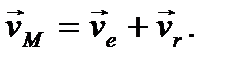(42)

Так как подвижная система координат движется поступательно, то переносная скорость точки равна скорости полюса А

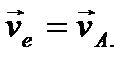
Относительным движением является вращение вокруг подвижной оси Аz. Обозначим относительную скорость 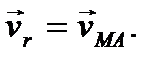Она направлена по касательной к относительной траектории (перпендикулярно отрезку АМ), согласуясь по направлению с угловой скоростью w (см. рис. 34). Величина относительной скорости в данном случае может быть найдена по формуле для вращательного движения

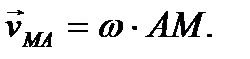
После этого выражение (42) можно записать в окончательном виде

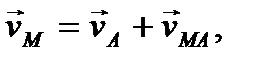(43)

выражающем доказываемую теорему.

С помощью доказанной теоремы можно определить скорость любой точки тела, если известны скорость полюса и угловая скорость тела. Еще одна теорема, позволяющая находить скорости точек тела при плоском движении, вытекает из предыдущей.

Теорема о проекциях скоростей точек тела

При плоском движении тела проекции скоростей двух любых его точек на ось, проведенную через эти точки, равны.

Доказательство

Для доказательства выберем на теле две произвольные точки А и В и проведем через эти точки ось Аx (см. рис. 35).

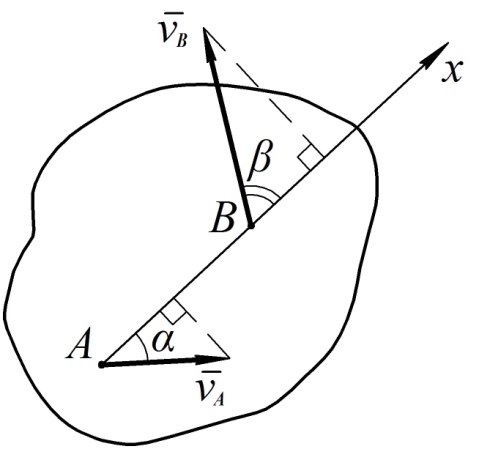
Рис 35

Запишем в соответствии с (43) выражение для скорости точки В, выбрав в качестве полюса точку А

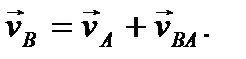(44)

Запишем теперь векторное равенство (43) в проекциях на ось Ах

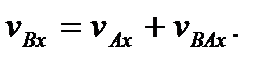
Учитывая, что вектор 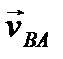перпендикулярен отрезку АВ ( 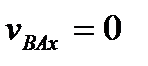), получим отсюда утверждение теоремы

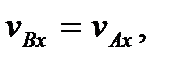(45)

которое еще можно переписать в виде (см. рис. 35)

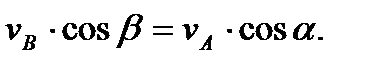
4.3. Мгновенный центр скоростей

Теорема о существовании мгновенного центра скоростей

В любой момент времени при плоском движении фигуры в ее плоскости, если 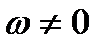, существует единственная точка подвижной плоскости, мысленно связанной с фигурой, скорость которой равна нулю. Эта точка называется мгновенным центром скоростей (МЦС).

Доказательство

При доказательстве теоремы укажем конкретный способ построения МЦС. Пусть известны скорость некоторой точки А плоской фигуры 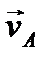и угловая скорость ω (см. рис.36). Проведем из точки А луч, повернув вектор скорости на угол 90° в направлении ω. Отложим на этом луче отрезок АР длиной

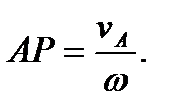
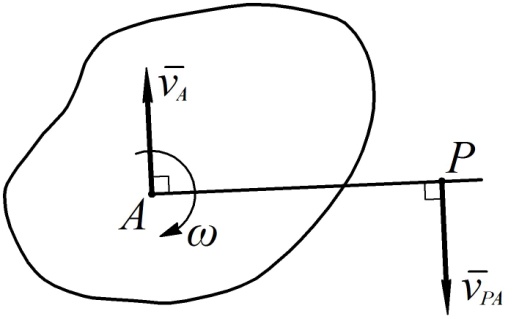
Рис. 36

Вычислим теперь скорость точки Р по теореме сложения скоростей

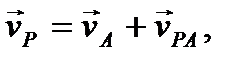
где вектор 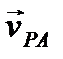перпендикулярен отрезку AP и направлен противоположно вектору 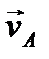. Найдем модуль вектора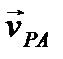

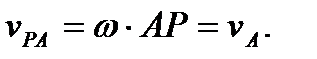
Таким образом, получаем, что 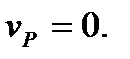Мгновенный центр скоростей (точка Р) построен. Теорема доказана.

Если мгновенный центр скоростей известен, то приняв его за полюс, для точки А плоской фигуры получим

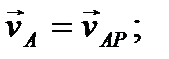
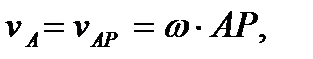(46)

причем скорость 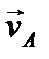перпендикулярна к отрезку АР. Аналогично и для любой другой точки В

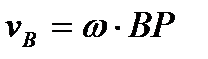(47)

и вектор 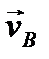перпендикулярен отрезку ВР ( см. рис. 37 ).

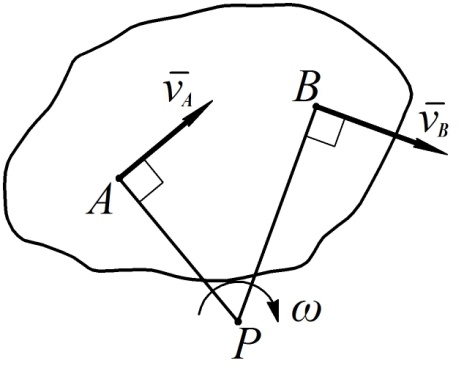
Рис. 37

Из (46) и (47) следует, что

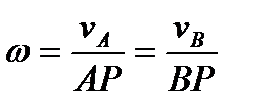(48)

и

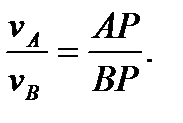(49)

Следовательно, скорости точек фигуры при плоском движении могут вычисляться как при вращении этой фигуры в данный момент вокруг мгновенного центра скоростей с угловой скоростью ω.

Таким образом, если построен МЦС и найдена угловая скорость, вычисление скоростей точек тела при плоском движении существенно упрощается. Угловая скорость обычно находится после построения МЦС по формуле (48). Рассмотрим далее основные способы построения МЦС.