Глава 2. простейшие движения твердого тела

Теоретическая механика

Курс лекций

Часть 1

Учебное пособие

Издание первое

Тверь 2011

УДК 531/534(075.8)

ББК 22.21я7

Клыков, В.Е. Теоретическая механика. Курс лекций. Часть 1: учеб. пособие/ В.Е. Клыков. Тверь: ТвГТУ, 2012. 118 с.

В учебном пособии компактно излагается первая часть курса теоретической механики (кинематика и статика). Содержание курса соответствует государственным образовательным стандартам для специальностей ТМС, ПГС, АДА, ПЗ, СДМО, ГМО, СТМ, где учебными планами предусмотрено изучение теоретической механики в течение двух учебных семестров. Материал излагается доступно и достаточно строго. Основные положения теории иллюстрируются примерами решения задач.

Пособие предназначено студентам соответствующих специальностей дневной и заочной форм обучения.

Рецензенты: зав. кафедрой СДМО ТвГТУ, доктор технических наук, профессор А.В. Кондратьев; профессор кафедры ремонта машин и ЭМТП ТГСХА, доктор технических наук В.В. Козырев.

ISBN © Тверской государственный

технический университет, 2012

© Клыков В.Е., 2012

Введение

Теоретическая механика – это наука, изучающая математическими методами механическое движение и равновесие материальных объектов. При этом изучаются не реальные материальные тела, а их идеализированные образы – материальная точка и абсолютно твердое тело.

Под материальной точкой понимают материальное тело, размерами которого можно пренебречь.

Абсолютно твердым телом называют такое материальное тело, геометрическая форма и размеры которого не изменяются при любых механических воздействиях со стороны других тел и расстояние между любыми двумя точками которого остается постоянным. В дальнейшем по тексту последний термин не всегда полностью воспроизводится, однако следует иметь в виду, что все рассматриваемые тела считаются абсолютно твердыми.

Такая идеализация изучаемых объектов в теоретической механике делает возможным широкое применение математических методов исследования.

Теоретическая механика имеет фундаментальное значение для науки и техники. На ее законах основываются такие крупные научные области как небесная механика, гидромеханика, механика деформируемого твердого тела. Многие технические науки, такие, как теория машин и механизмов, сопротивление материалов, строительная механика, теория гироскопов и другие, опираются в первую очередь на выводы теоретической механики. Все это делает теоретическую механику одной из важнейших дисциплин инженерно-технического образования.

Содержание теоретической механики включает в себя три раздела: кинематику, статику и динамику. В указанном порядке эти разделы будут рассмотрены далее.

Раздел 1. КИНЕМАТИКА

Кинематика – это раздел теоретической механики, в котором изучается движение материальных объектов с геометрической стороны вне связи с причинами, вызывающими движение.

Глава 1. КИНЕМАТИКА ТОЧКИ

1.1. Векторный способ задания движения точки

Положение точки можно характеризовать радиусом-вектором r , который начинается в выбранной неподвижной точке О и заканчивается в точке М, движение которой изучается (рис. 1). При векторном способе задания движения точки её радиус-вектор задаётся как функция времени t:

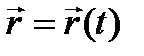. (1)

Уравнение (1) называют векторным уравнением движения точки. Векторная функция в правой его части должна быть дважды дифференцируема.

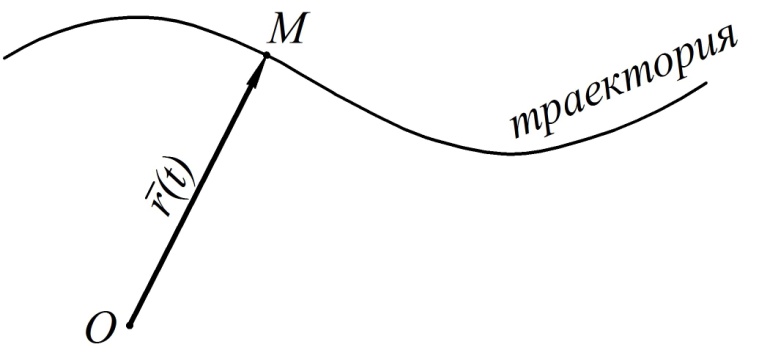
Рис. 1

Покажем далее, как, используя уравнение (1), найти кинематические характеристики движения точки. Попутно дадим определения этим характеристикам движения.

Линия, которую описывает точка при своём движении, называется траекторией. Траектория точки в данном случае может быть найдена как годограф радиус-вектора.

Годографом переменного вектора называется геометрическое место концов этого вектора, если его последовательные положения, получающиеся при изменении аргумента, откладывать из одной неподвижной точки.

Средней скоростью точки за промежуток времени Δt называется вектор

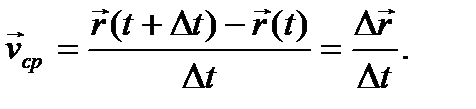
Мгновенной скоростью (или просто скоростью) точки в момент времени t называется вектор

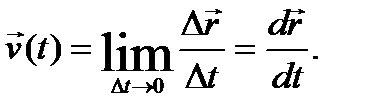(2)

Векторы средней и мгновенной скорости показаны на рис. 2.

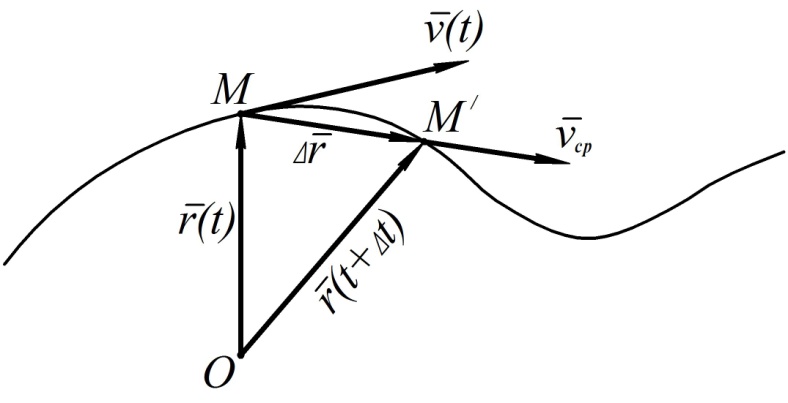
Рис. 2

Вектор скорости характеризует быстроту и направление движения точки. Он направлен по касательной к траектории точки в сторону движения.

Аналогично определяются векторы среднего и мгновенного ускорения точки:

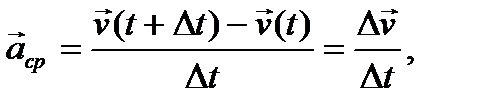
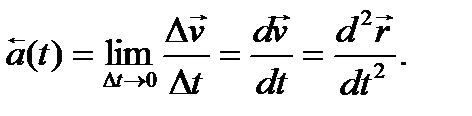(3)

Векторы среднего и мгновенного ускорений показаны на рис. 3.

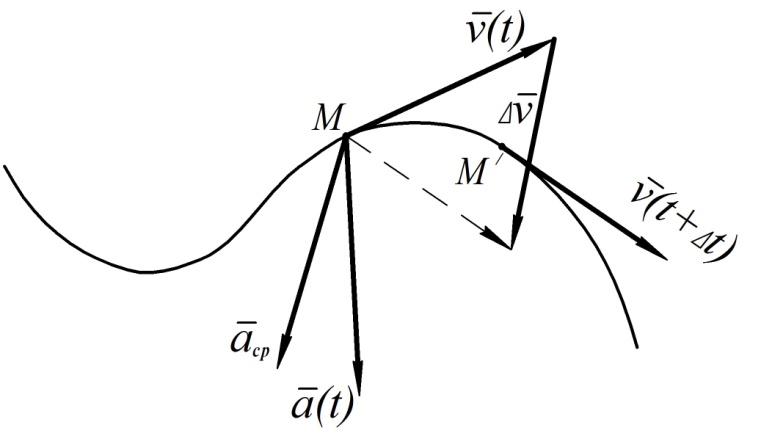
Рис. 3

Вектор ускорения характеризует изменение вектора скорости по величине и по направлению. Он отклонен от касательной к траектории в сторону её вогнутости. При прямолинейном движении точки векторы скорости и ускорения направлены вдоль траектории точки.

Задание движения точки в декартовых координатах

При этом способе задания движения задаются декартовы координаты точки как функции времени:

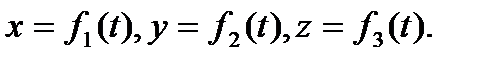(4)

Уравнения (4) называют кинематическими уравнениями движения точки в декартовых координатах. Функции, стоящие в правых частях этих уравнений, должны быть дважды дифференцируемыми. При движении точки в плоскости достаточно задать два кинематических уравнения движения.

Покажем, как с помощью уравнений (4) можно найти все характеристики движения точки.

Для нахождения траектории нужно из уравнений (4) исключить параметр t. Если точка движется в пространстве, то после исключения t из уравнений (4) получим два уравнения вида

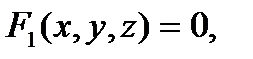
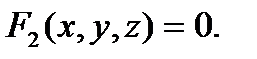
Эти уравнения определяют в пространстве линию, которая будет траекторией точки. Если точка движется в плоскости, то после исключения t из первых двух уравнений (4) получим одно уравнение вида

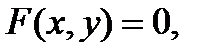
которое определяет линию в плоскости (x,y).

Для нахождения скорости и ускорения точки выразим её радиус-вектор через декартовы координаты. Если в точке О, из которой откладывается радиус-вектор, выбрать начало декартовой системы координат, то легко получить выражение (рис. 4)

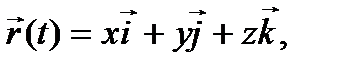(5)

где 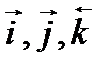– орты координатных осей.

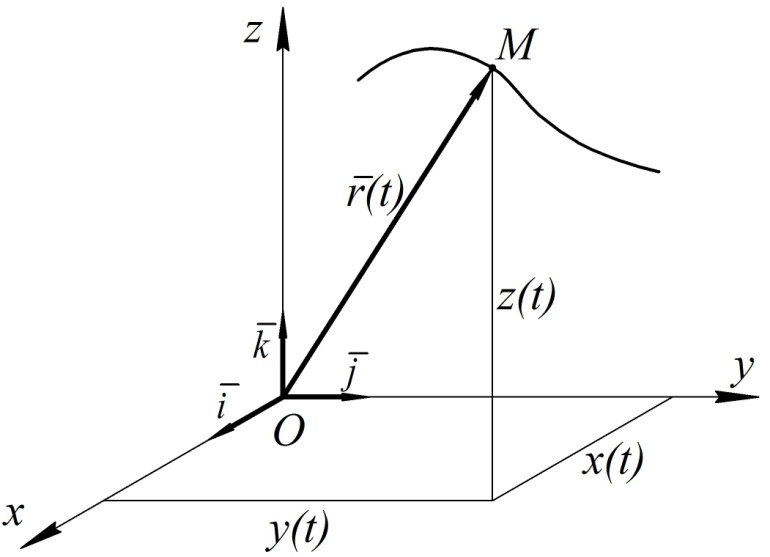
Рис. 4

Продифференцировав равенство (5) по времени, получим

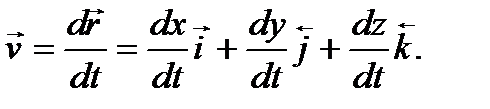(6)

Обозначая производные по времени точками над дифференцируемой функцией ( 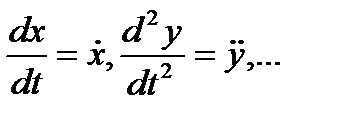), из последнего выражения получим формулы для проекций скорости на оси координат

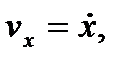
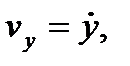
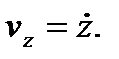(7)

Величина скорости после этого найдется через её проекции

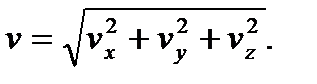
Повторно дифференцируя равенство (6) по времени, получим

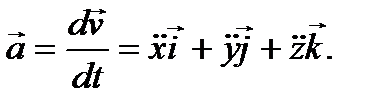
Отсюда проекции ускорения на оси координат

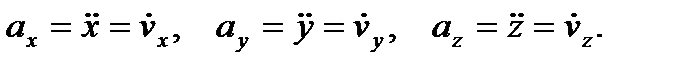(8)

По этим проекциям определяем величину вектора ускорения

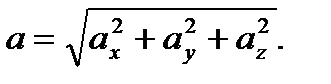
Пример 1

Движение точки в плоскости задано уравнениями

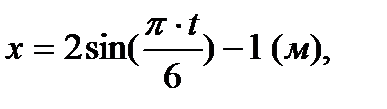
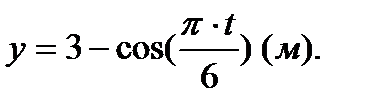
Требуется определить траекторию точки, а также для момента времени 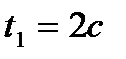найти положение точки, скорость и ускорение.

Решение

Для исключения t из кинематических уравнений движения воспользуемся основным тригонометрическим тождеством 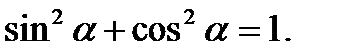Из уравнений движения выразим

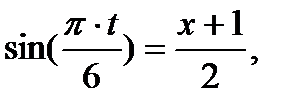
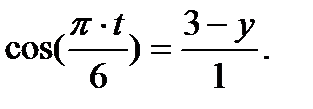
После возведения в квадрат этих выражений и почленного сложения полученных равенств найдем уравнение траектории в виде

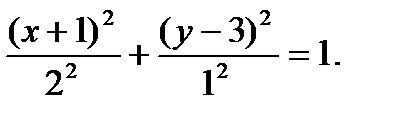
Это уравнение эллипса. Построим его на рис. 5.

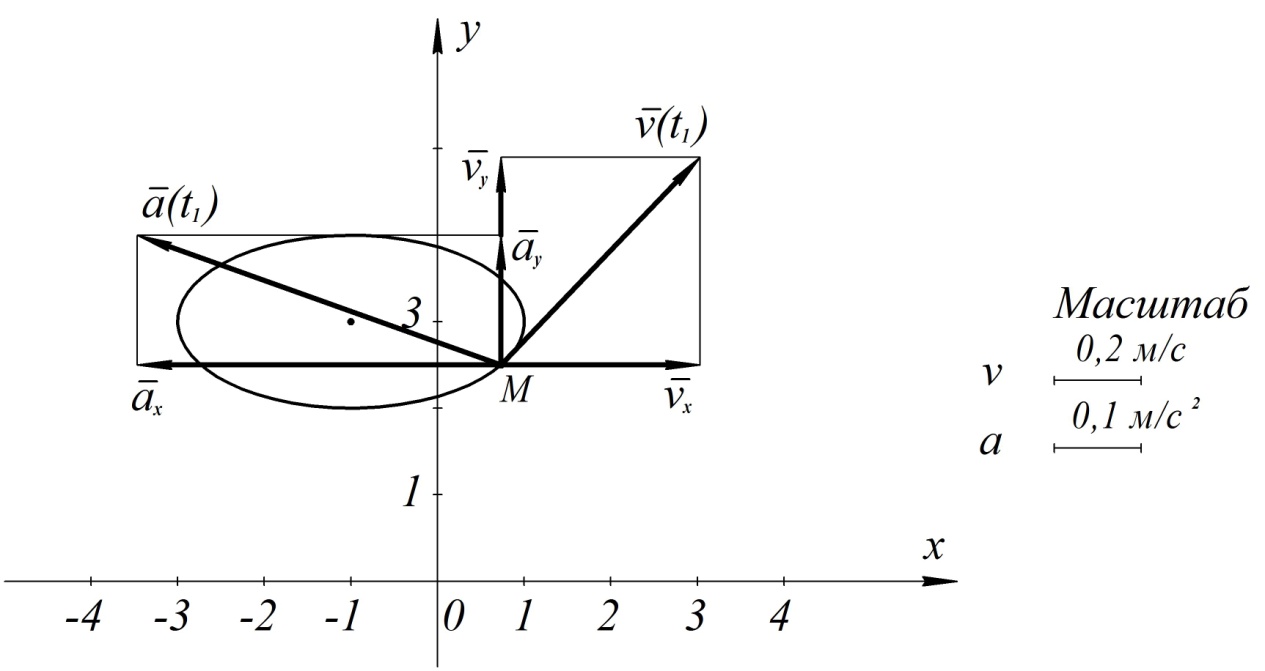
Рис. 5

Положение точки в момент 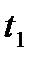определяется её координатами:

.

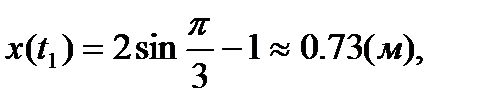
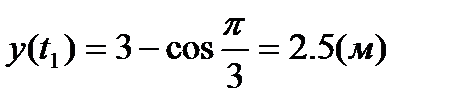Векторы скорости и ускорения точки найдем через их проекции на оси координат по формулам (7) и (8)

;

;

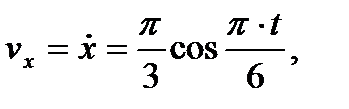
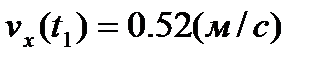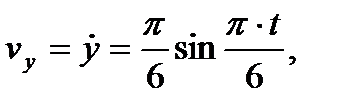
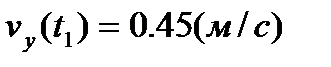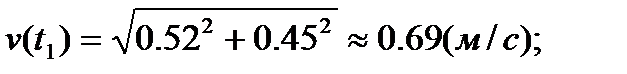
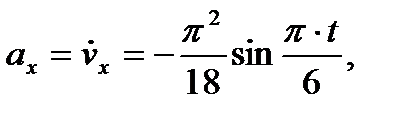
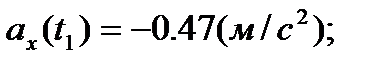
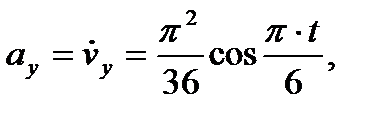
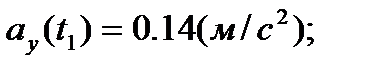
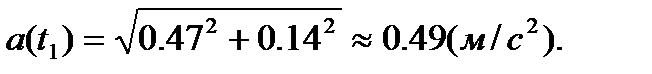
Построим теперь векторы скорости и ускорения в выбранном масштабе на рис. 5, показав их в найденном положении точки на траектории.

Задание движения точки естественным способом

В этом случае должны быть заданы (рис. 6):

траектория точки,

начало отсчета дуговой координаты s (точка О) на траектории и положительное направление её отсчета,

кинематическое уравнение движения в виде

s=f(t). (9)

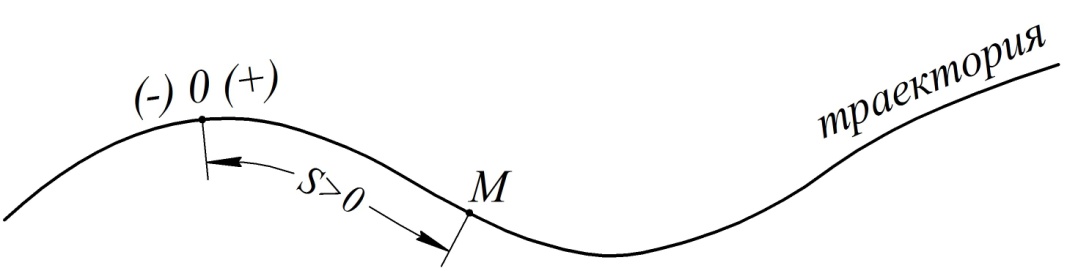
Рис. 6

При данном способе задания движения точки используется естественная система координат, начало которой связано с движущейся точкой (рис. 7). Эта система координат имеет следующие оси:

касательная к траектории ( );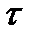

главная нормаль (n), проходящая через центр кривизны траектории;

бинормаль (b).

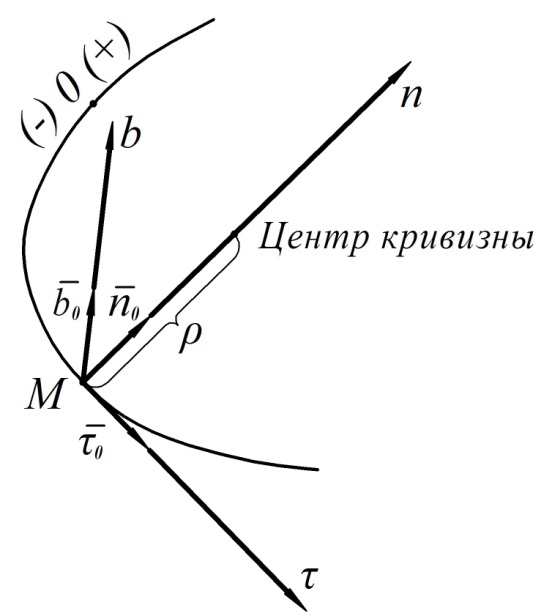
Рис. 7

Найдем вектор скорости:

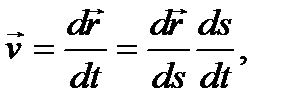
где

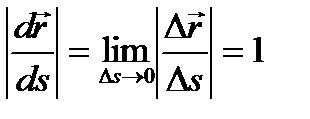
как предел отношения бесконечно малой дуги к стягивающей её хорде. Направление вектора 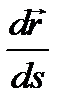установим с учетом того, что вектор 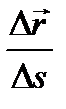направлен по 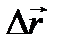при Δs>0 и противоположно 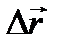при Δs<0, т. е. вектор 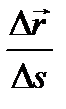по хорде в сторону возрастания дуговой координаты s. Следовательно, единичный вектор 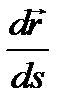направлен по касательной к траектории в направлении оси τ. Обозначим этот орт оси τ через 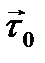. Тогда для скорости точки получим

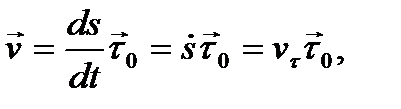(10)

где 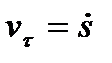– проекция вектора скорости на ось τ, называемая алгебраической скоростью. Для модуля скорости в данном случае справедлива формула

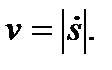
Прежде чем находить ускорение точки, выведем одну вспомогатель-ную формулу для производной от вектора постоянного модуля по скаляр-ному аргументу.

Рассмотрим вектор 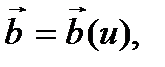где u – некоторый скалярный аргумент. Пусть вектор 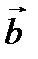имеет постоянный модуль 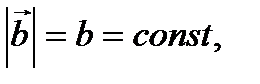то есть может изменять только своё направление. По определению производной

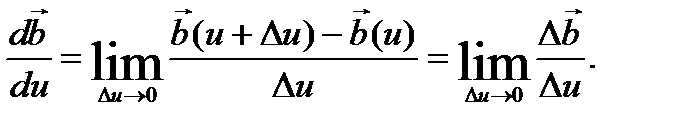
Для определения 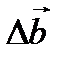из точки О отложим векторы 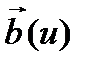и 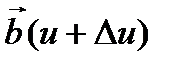(рис. 8) и

соединим их концы А и В. Угол поворота вектора 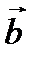обозначим 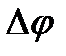. Из равнобедренного треугольника АОВ

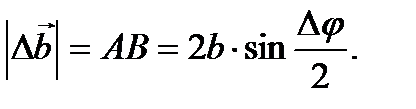
Для модуля искомой производной получим:

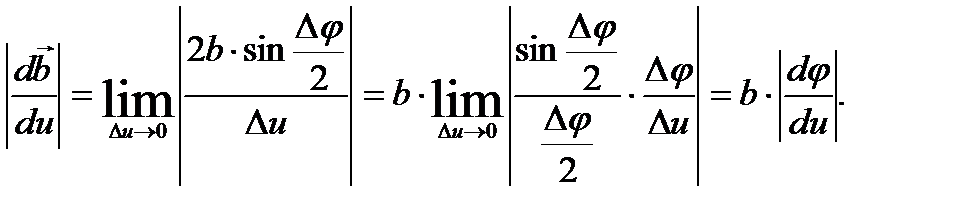
Отметим, что 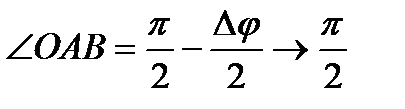при 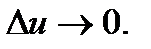Следовательно, вектор 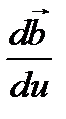направлен перпендикулярно к дифференцируемому вектору 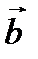в сторону его поворота при изменении аргумента u (рис. 8).

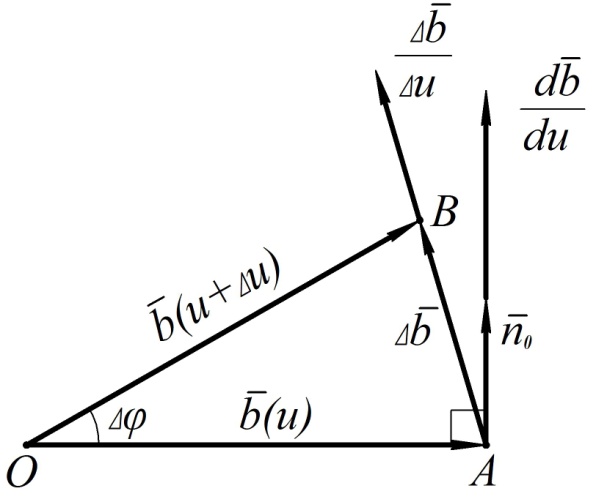
Рис. 8

Окончательно получим формулу

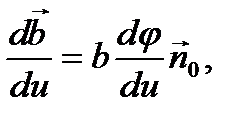(11)

где 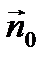– единичный вектор, совпадающий по направлению с вектором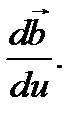

Если скалярным аргументом является время t, то

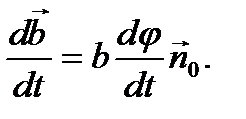
Правую часть этой формулы можно записать в виде векторного произведения двух векторов:

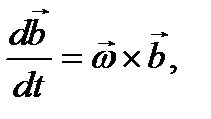(12)

где 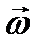– угловая скорость поворота вектора 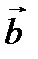. Величина угловой скорости 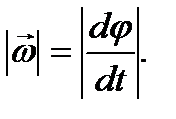Вектор 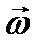следует направить перпендикулярно плоскости, в которой расположены векторы 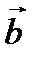и 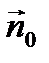, в ту сторону, откуда поворот вектора 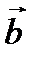виден против часовой стрелки.

Определим теперь ускорение точки как производную от вектора скорости по времени, продифференцировав выражение (10):

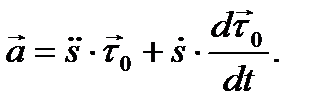
Преобразуем выражение для производной 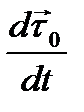с использованием формулы (11):

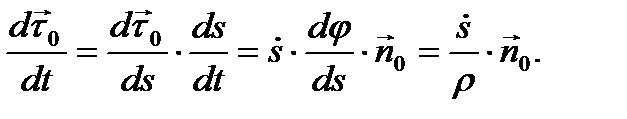
Здесь кривизна траектории 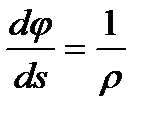выражена через радиус кривизны 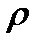. Окончательно для ускорения точки получим векторную формулу

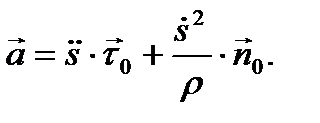(13)

Отсюда следует, что вектор ускорения точки имеет следующие проекции на оси естественной системы координат:

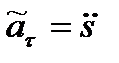- проекция ускорения на касательную к траектории, характеризующая изменение вектора скорости по величине;

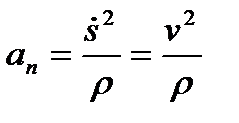– проекция ускорения на главную нормаль (нормальное ускорение), характеризующая изменение вектора скорости по направлению;

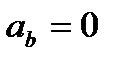– проекция ускорения на бинормаль, равная нулю при любом движении точки.

Величину 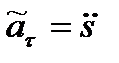, которая может быть как положительной, так и отрицательной, обычно называют алгебраическим значением тангенциального (касательного) ускорения, а величину 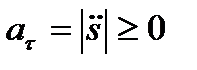называют тангенциальным (касательным) ускорением.

Модуль ускорения вычисляется по формуле

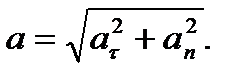(14)

Все найденные выше характеристики движения точки показаны на рис. 9.

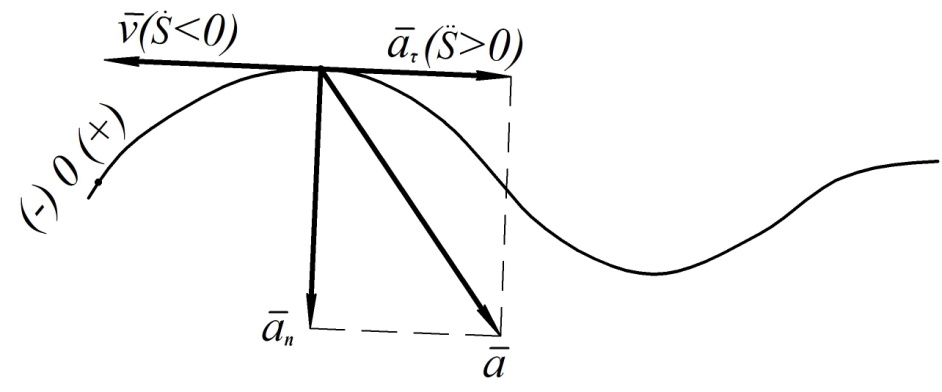
Рис. 9

Если векторы 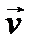и 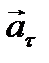направлены в одну сторону, то движение точки называется ускоренным. В противном случае движение точки называют замедленным.

Отметим, что тангенциальное ускорение можно найти и при задании движения точки в декартовых координатах:

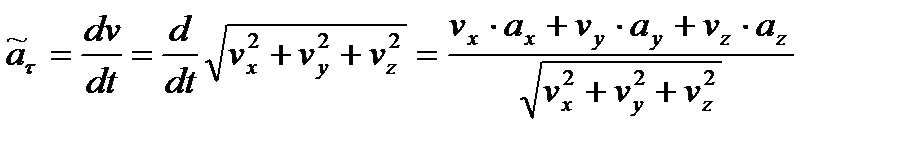
или

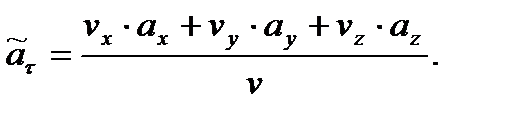(15)

Найденное по формуле (15) алгебраическое значение тангенциального ускорения может быть как положительной, так и отрицательной величиной. При этом 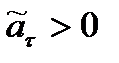соответствует ускоренному, а 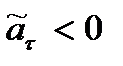– замедленному движению точки.

Путь, пройденный точкой за промежуток времени 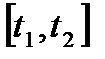, может быть вычислен по формуле

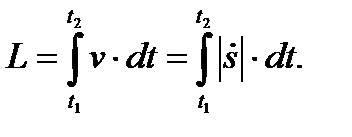(16)

Далее рассмотрим кратко простейшие случаи движения точки. К ним относятся равномерное и равнопеременное движения.

Признаком равномерного движения является 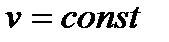. В этом случае при выборе начала отсчета дуговой координаты в начальном положении точки (при t=0) и положительного направления ее отсчета в направлении скорости получим

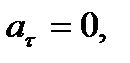
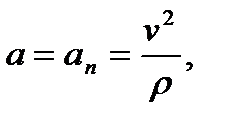
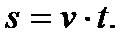
Признаком равнопеременного движения является 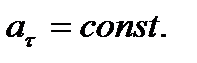В этом случае при том же выборе начала отсчета и положительного направления отсчета дуговой координаты получим

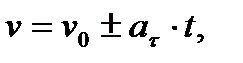
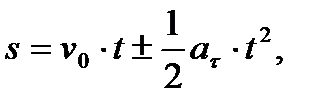
где 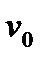– начальная скорость точки, 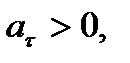знак « + » соответствует равноускоренному движению, знак « − » – равнозамедленному.

Пример 2

Движение точки задано кинематическим уравнением

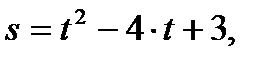
где s измеряется в метрах, а t – в секундах. Требуется определить путь, пройденный точкой за 4 секунды после начала движения.

Решение

Вычислим сначала производную

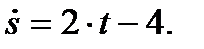
Далее по формуле (16) имеем

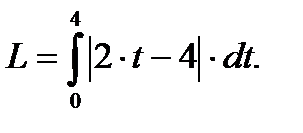
Чтобы избавиться от модуля под знаком интеграла, построим график функции на рис. 10.

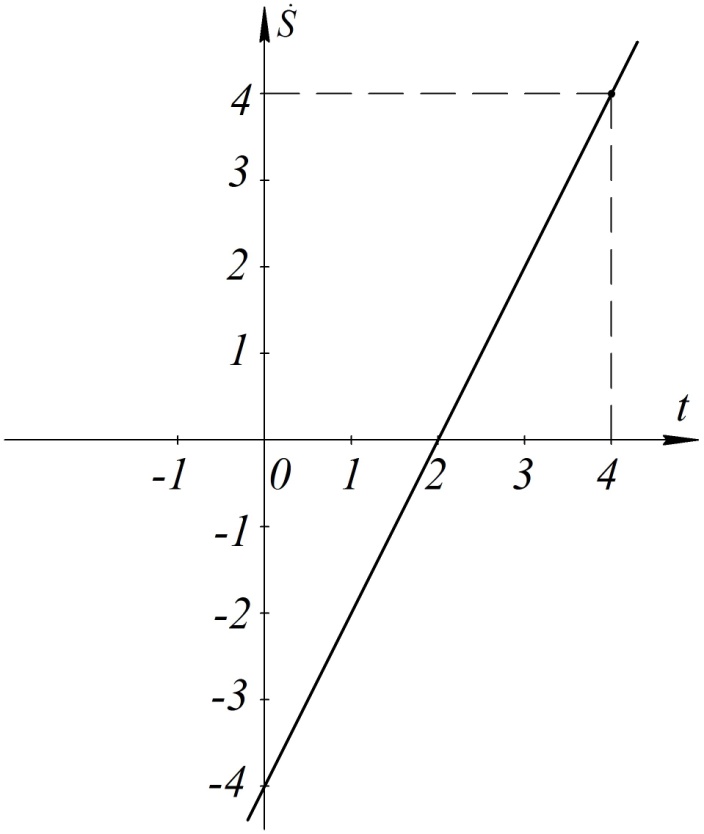
Рис. 10

Теперь можно опустить модуль под знаком интеграла, разбив промежуток интегрирования на две части, и провести вычисления:

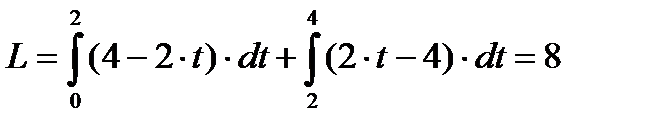(м).

Основные понятия

Движение твердого тела называется вращательным, если найдутся, по крайней мере, две точки, неизменно связанные с телом, которые остаются неподвижными во все время движения.

Прямая, проходящая через эти неподвижные точки, называется осью вращения. При вращательном движении точки тела, не лежащие на оси вращения, движутся по окружностям, расположенным в плоскостях, перпендикулярных к оси вращения с центрами на этой оси. Скорости точек, расположенных на оси вращения, равны нулю. На оси вращения обычно выбирают положительное направление (ось z, рис. 12).

Рис. 12

Проведем через ось вращения две полуплоскости: неподвижную Н и неизменно связанную с телом П. Положение полуплоскости П, а следовательно, и всего тела, можно задать линейным углом двугранного угла между полуплоскостями Н и П (рис. 12). Угол считается положительным, если он отсчитан от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси вращения. Будучи отсчитанным по часовой стрелке, угол считается отрицательным.

Введенный таким образом угол называется углом поворота тела. Если угол поворота задать как функцию времени, то полученное уравнение называют кинематическим уравнением вращательного движения твердого тела :

(20)

При изучении движения тела характеристики движения подразделяются на глобальные (одинаковые для всех точек тела) и локальные (различные для разных точек тела). Покажем далее, как с помощью уравнения (20) найти все эти характеристики движения.

2.2.2. Угловая скорость и угловое ускорение тела

Средней угловой скоростью тела за промежуток времени называется

Мгновенной угловой скоростью (или просто угловой скоростью) тела в момент времени t называется

(21)

Определяемая по формуле (21) угловая скорость может принимать положительные и отрицательные значения. Поэтому величина называется алгебраическим значением угловой скорости. Угловая скорость как физическая характеристика движения считается положительной и определяется выражением

Угловая скорость характеризует быстроту вращения тела.

Аналогично определяются среднее и мгновенное угловые ускорения:

(22)

Угловое ускорение характеризует быстроту изменения угловой скорости. Угловая скорость и угловое ускорение являются глобальными характеристиками движения, их часто обозначают дуговыми стрелками, охватывающими ось вращения и указывающими направление соответствующих характеристик движения (рис. 13).

Иногда угловую скорость и угловое ускорение изображают в виде векторов, которые по модулю равны соответствующим физическим характеристикам и направлены вдоль оси вращения по правилу правого винта. Направив вдоль оси вращения ось z так, чтобы при взгляде навстречу этой оси положительное направление отсчета угла было видно против часовой стрелки, можно для введенных векторов написать соотношения

Рис. 13

2.2.3. Простейшие случаи вращательного движения твердого тела

Отметим два важных простейших случая вращательного движения тела.

1. Равномерное вращение. Оно характеризуется постоянной угловой скоростью w=const. В этом случае угловое ускорение e=0 и угол поворота определяется по формуле

Здесь и далее считается, что начальному положению тела при t=0 соответствует угол j=0.

2. Равнопеременное вращение. Оно характеризуется постоянным угловым ускорением e=const. В этом случае угловая скорость и угол поворота тела рассчитываются по формулам

Здесь – начальная угловая скорость, знак « + » соответствует равноускоренному вращению, знак « − » – равнозамедленному.

2.2.4. Определение скоростей и ускорений точек тела

Пусть задано кинематическое уравнение вращательного движения тела Зададим движение произвольной точки М тела естественным способом. Начало отсчета дуговой координаты на траектории выберем в точке пересечения траектории с неподвижной полуплоскостью Н (см. рис. 14). Положительное направление отсчета дуговой координаты s совместим с положительным направлением отсчета угла поворота j.

Рис. 14

Тогда уравнение движения точки М по ее траектории примет вид

где h – расстояние от точки М до оси вращения (радиус окружности, по которой движется точка).

Для алгебраической скорости точки М получим

Модуль скорости точки определится по формуле

(23)

Вектор скорости точки М будет направлен по касательной к траектории, согласуясь с направлением угловой скорости.

Тангенциальное и нормальное ускорения точки найдутся по формулам

(24)

Тангенциальное ускорение будет направлено по касательной к траектории точки, согласуясь с направлением углового ускорения e. Нормальное ускорение направлено перпендикулярно касательной к оси вращения. Полное ускорение найдется по теореме Пифагора

(25)

Направление векторов скорости и ускорения показано на рис. 15.

Найдем угол a между векторами полного и нормального ускорения точки:

Рис. 15

Из этой формулы следует, что угол a для всех точек тела в любой момент времени одинаков.

2.2.5. Векторные формулы для скоростей и ускорений точек тела

Рассмотрим точку М вращающегося тела, положение которой определяется радиусом-вектором относительно полюса О, взятого на оси вращения (рис. 16). Докажем, что скорость этой точки может быть выражена в виде векторного произведения по формуле Эйлера:

(26)

Заметим сразу, что в данном случае где вектор не изменяется по величине (тело считается абсолютно твердым), но изменяет свое направление, поворачиваясь с угловой скоростью . Поэтому с использованием формулы Эйлера (26) можно вычислять производную по времени от произвольного вектора , не изменяющегося по величине:

Это выражение совпадает с полученной ранее формулой (12).

Рис 16

Вернемся к доказательству формулы (26). Для модуля скорости имеем

Направление вектора скорости тоже соответствует направлению векторного произведения в формуле (26).

Найдем далее вектор ускорения точки М как производную от вектора скорости по времени:

или окончательно

(27)

Для модуля вектора имеем

Направление векторного произведения тоже совпадает с направлением тангенциального ускорения. Таким образом, первое слагаемое в правой части (27) есть вектор тангенциального ускорения.

Найдем теперь модуль вектора :

В соответствии с правилом векторного произведения направление этого вектора тоже совпадает с направлением нормального ускорения, то есть второе слагаемое в правой части (27) равно вектору нормального ускорения.

Таким образом, для ускорения точек вращающегося тела справедливы векторные формулы:

(28)

Пример 3

Груз опускается вертикально вниз, двигаясь по закону м (t – в с). Он приводит во вращение ступенчатый шкив 1, посредством которого движение передается диску 2 (рис.17). Определить скорость и ускорение точки А, лежащей на ободе диска 2, в момент времени с, если скольжение между дисками отсутствует. Заданы радиусы м, м, м.

Рис. 17

Решение

Найдем вначале скорость груза Точка С схода нити будет иметь такую же скорость. Теперь можно найти угловую скорость шкива 1

Далее можно последовательно найти скорость точки зацепления дисков

угловую скорость диска 2

его угловое ускорение

а также искомые скорость и ускорение точки А:

Вычислив искомые величины при сек, получим окончательный ответ:

,

Покажем все найденные характеристики движения на рисунке.

Основные понятия

Пусть в пространстве движется материальная точка. Выберем две движущиеся друг относительно друга системы координат. Одну из них 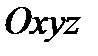назовем основной (неподвижной), а другую 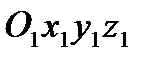– подвижной – (рис. 18). Дадим далее ряд определений.

Движение точки, наблюдаемое из основной системы координат (то есть, видимое наблюдателем, связанным с осями 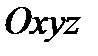), называется абсолютным (или сложным) движением .

Соответствующие характеристики движения (наблюдаемые указанным наблюдателем) будем обозначать общепринятыми буквами без индексов. Например, через v будем обозначать абсолютную скорость точки, наблюдаемую из основной системы координат, через а – абсолютное ускорение и т. д.

Движение точки, наблюдаемое из подвижной системы координат (видимое наблюдателем, связанным с осями 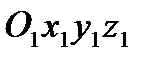), называется относительным движением.

Соответствующие характеристики движения будем обозначать с индексом r . Например, через 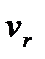будем обозначать относительную скорость точки, наблюдаемую из подвижной системы координат и т. д.

Движение подвижной системы координат и всех жестко связанных с ней точек, наблюдаемое из основной системы координат, называется переносным движением.

Соответствующие характеристики движения будем обозначать с индексом е. Например, через 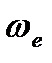будем обозначать переносную угловую скорость (угловую скорость подвижной системы координат, наблюдаемую из основной системы координат), через 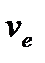– переносную скорость точки в каком-либо ее положении (скорость точки, мысленно скрепленной с подвижной системой координат в данном ее положении, то есть, скорость точки, у которой в данном положении мысленно остановлено относительное движение) и т. д.

На практике обычно основную систему координат связывают с поверхностью Земли, поэтому ее часто называют неподвижной (относительно Земли).

При решении практических задач бывает полезно мысленно себе представить и построить на рисунке абсолютную, относительную и переносную траектории точки.

Приведем несколько примеров.

Пусть прямолинейная трубка вращается в плоскости рисунка и в трубке движется шарик М, удаляясь от оси вращения (см. рис. 18). Свяжем основную систему координат с основанием, на котором крепится ось вращения. Подвижную систему координат свяжем с трубкой. Изобразим на рисунке абсолютную, относительную и переносную траектории. Как видно из рисунка, в данном случае относительная (прямая линия) и переносная (окружность) траектории являются более простыми линиями, а абсолютная траектория (спираль) является более сложной, то есть, в результате сложения двух простых движений (по прямой и по окружности) получается более сложное движение (по спирали).

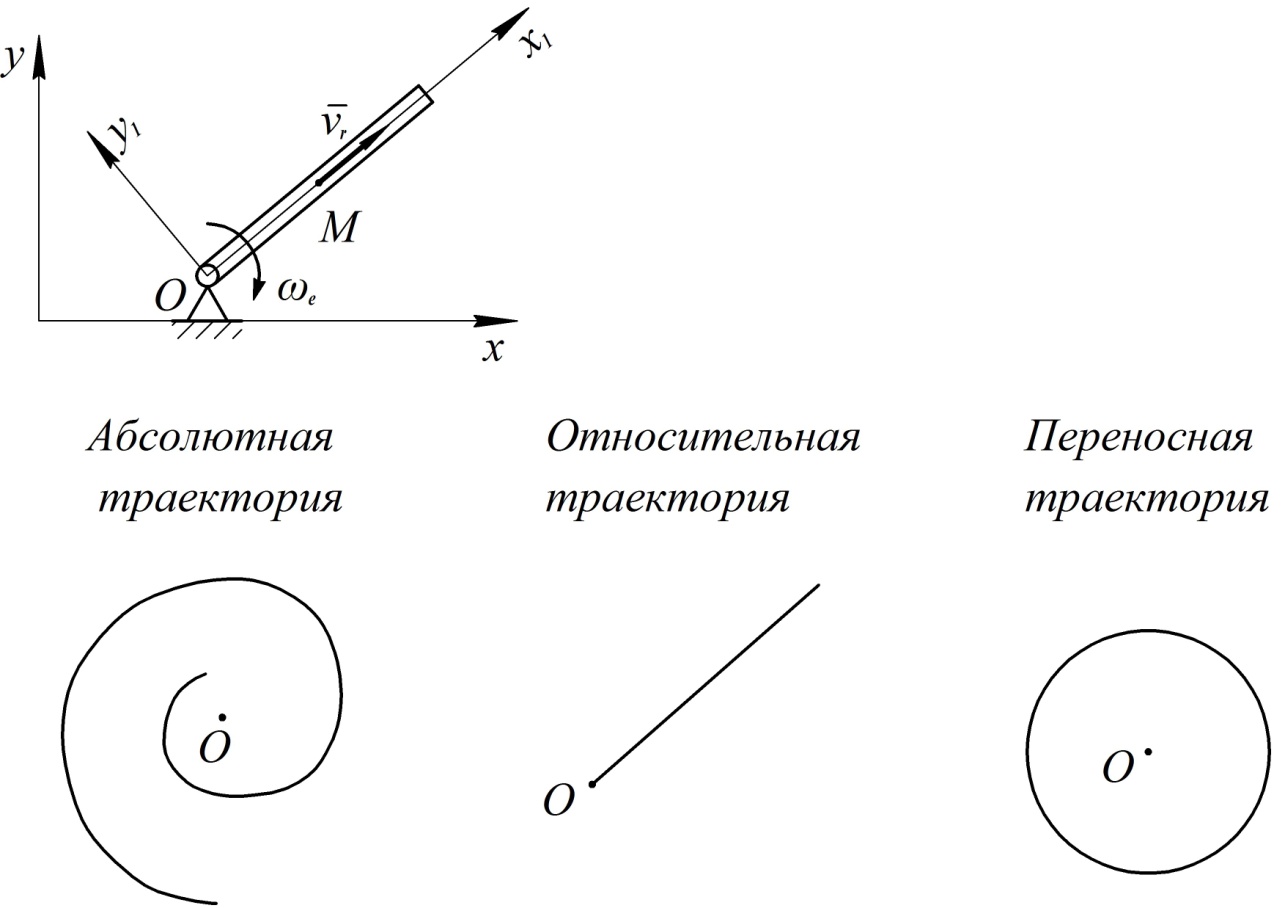
Рис. 18

В следующем примере представим себе горизонтальный диск, вращающийся вокруг вертикальной оси (карусель), и камень М, падающий вертикально вниз на земную поверхность. Основную систему координат свяжем с поверхностью Земли. Подвижную систему координат свяжем с диском (рис. 19). Изобразим на рисунке абсолютную, относительную и переносную траектории.

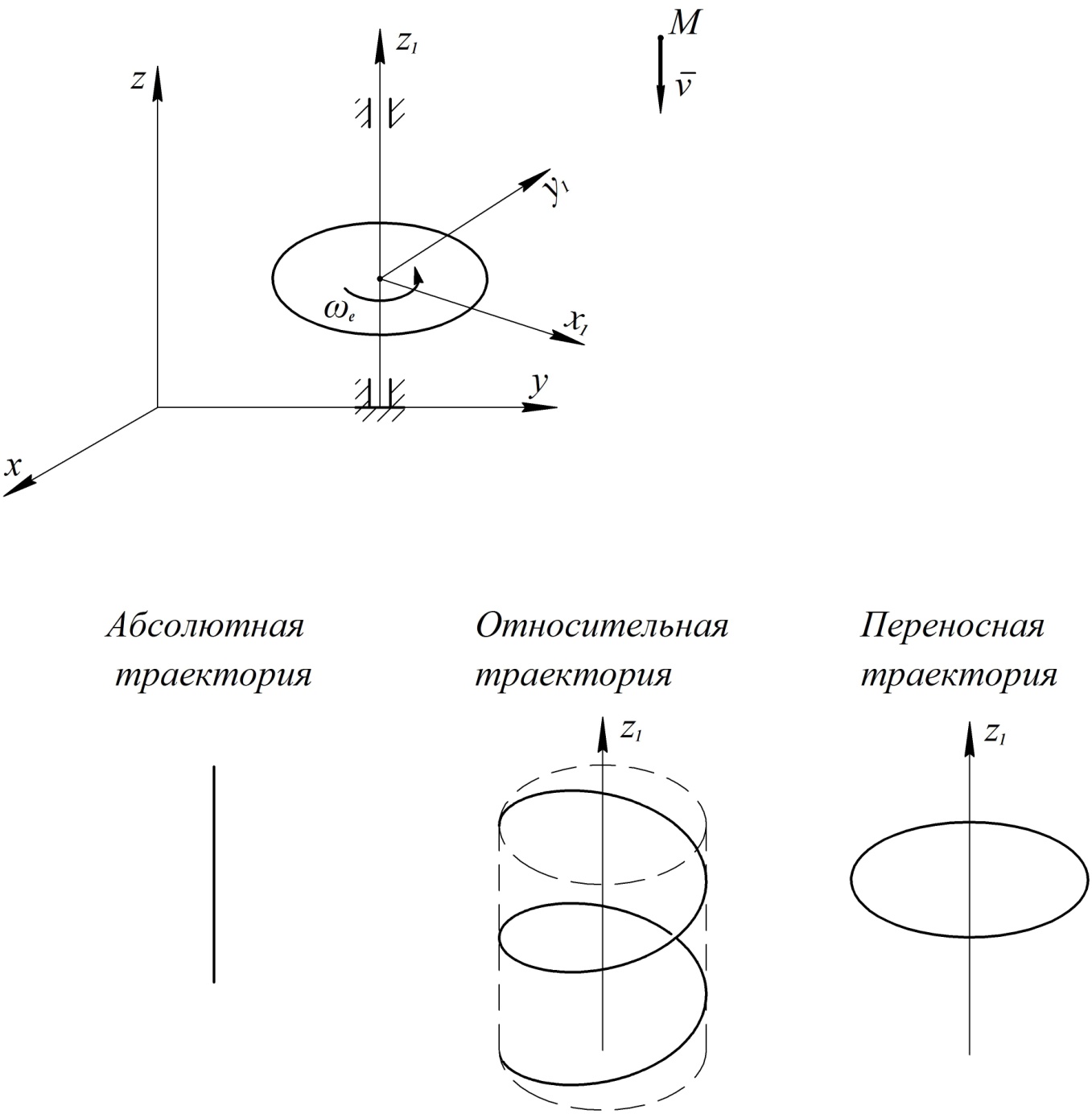
Рис. 19

Здесь абсолютная траектория (вертикальная прямая) является простой линией, а относительная (нисходящая спираль на поверхности цилиндра) и переносная (окружность) траектории являются более сложными. В данном случае в результате сложения двух сложных движений (по спирали и по окружности) получается более простое (по прямой).

Пример 4

По грани призмы, движущейся влево со скоростью 2 м/с, скользит конец А стержня АВ (рис. 23). Задан угол 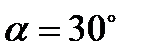. Найти скорость скольжения точки А относительно призмы.

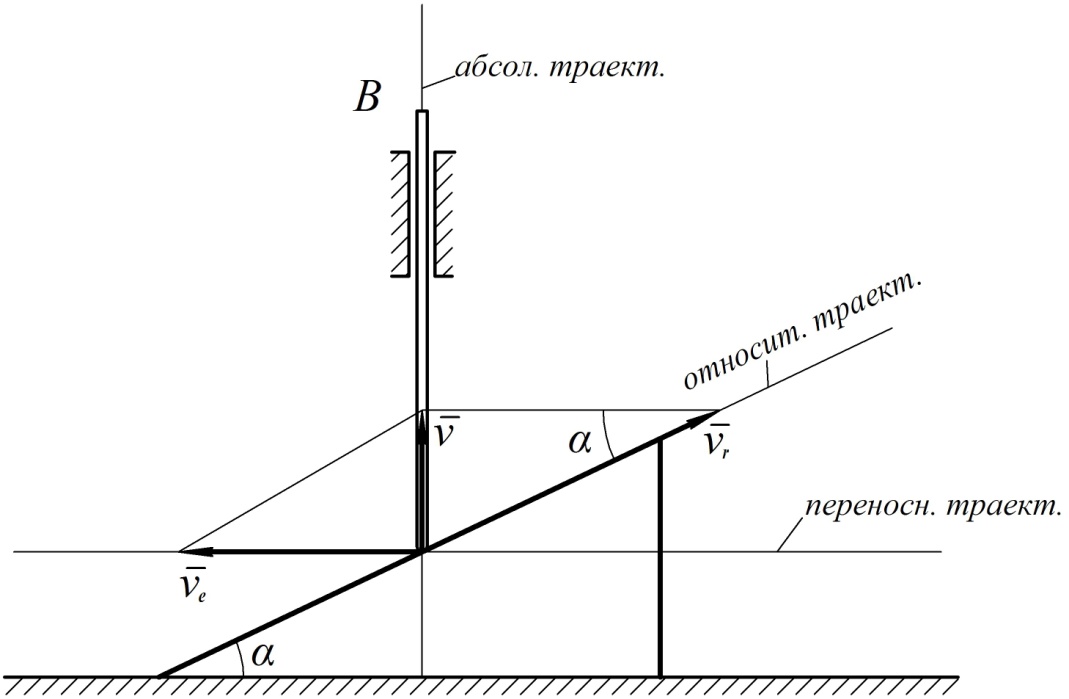
Рис. 23

Решение

Рассмотрим движение точки А как сложное. Свяжем подвижную систему координат с призмой. Проведем через точку А относительную, переносную и абсолютную траектории. Учитывая, что переносная скорость 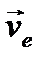(заданная скорость призмы) направлена влево, построим параллелограмм, соответствующий векторному равенству:

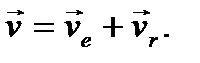
Из рисунка следует, что

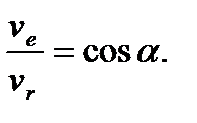
Отсюда находим искомую относительную скорость

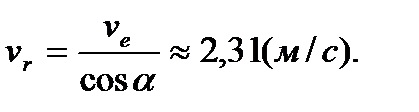
Пример 5

Прямолинейная трубка прикреплена к вертикальной оси под углом и вращается вокруг нее по закону 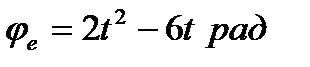. Вдоль трубки по закону 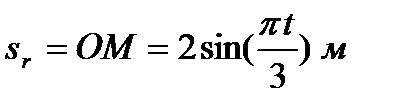движется шарик М (см. рис. 28). Положительное направление отсчета угла 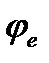показано на рисунке дуговой стрелкой, 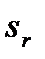считается положительным вниз по трубке от точки О. Требуется определить величину абсолютного ускорения точки М в момент времени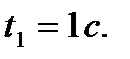

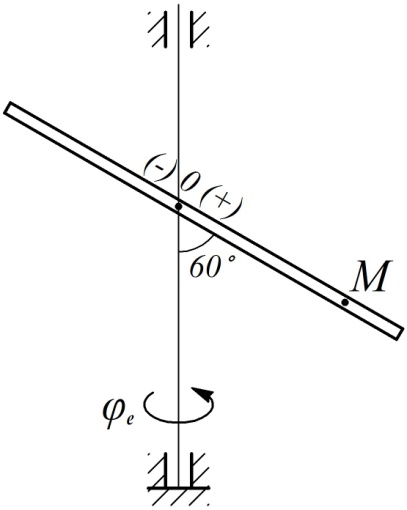
Рис. 28

Решение

Мысленно свяжем подвижную систему координат с трубкой. Тогда переносн