Определение размеров и нагружения конструкции.

Первой буквой шифра задания на курсовую работу указывается схема расположения подкосов. В нашем случае это буква A, а это значит, что диагональный подкос соединяет узлы 3` и 7.

По цифрам в шифре определяем геометрию конструкции и её нагружения:

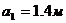
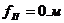
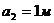
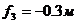
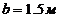
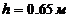
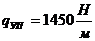
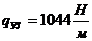
Проектировочный расчёт подкосного крыла.

Раскрытие статической неопределимости и выбор основной системы подкосного крыла.

Для плоско-пространственной ферменно-балочной закрепленной стержневой системы степень статической неопределимости k подсчитывается по формуле:

,

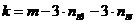Где 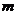- число стержней конструкции (включая опорные).

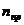-число «пространственных» узлов.

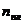-число «плоских» узлов.

В нашем случае по схеме находим, что 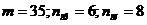. Следовательно, получаем:

;

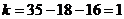Т.е. плоское крыло представляет собой один раз статически-неопределимую стержневую систему.

Раскрытие статической неопределимости выполним методом сил. Для этого выберем условно-необходимый «лишний» стержень и мысленно его разрежем. Целесообразней всего в качестве такого стержня выбрать диагональный подкос 3`-7.

Таким образом, мы получаем основную систему статически-неопределимого подкосного крыла, которая представлена на (рис. 1).

Исследование геометрической неизменяемости основной системы подкосного крыла.

Исследование основной системы на геометрическую неизменяемость выполним на вспомогательной конструкции - пространственной ферме, по геометрической неизменяемости эквивалентной исходной плоско-пространственной комбинированной стержневой системе.

Эквивалентную по геометрической неизменяемости пространственную ферму получим следующим образом:

1) в узлах 2 и 2` вводим пространственные шарниры;

2) ставим два дополнительных стержня 2 - 7 и 2` - 7` для ликвидации возможности перемещения узлов 2 и 2` в плоскости YOZ;

3) отбрасываем геометрически неизменяемую консольную часть плана подкосного крыла.

Полученную таким образом эквивалентную по геометрической неизменяемости пространственную ферму (рис. 2) и будем исследовать на геометрическую неизменяемость.

Исследование произведем способом нулевой нагрузки, который гласит:

- если при отсутствии внешней нагрузки все узлы фермы находятся в равновесии и при ненулевых усилиях в стержнях, то такая ферма ГН;

- если при отсутствии внешней нагрузки узлы фермы находятся в равновесии и при ненулевых усилиях в стержнях, то такая ферма ГИ.

Плоских узлов нет.

1. 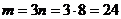т.е. условие минимума выполняется.

2. ферма простейшая, т.к. получена путем последовательного присоединения элементарных узлов к первооснове.

Таким образом, получили, что эквивалентная ферма геометрически неизменяема. Следовательно, и основная система статически неопределимого крыла также геометрически неизменяема.