Исследование простейшей САУ - физическая модель

Введение

Представленные в данном методическом пособии работы обеспечивают лабораторную поддержку для основных разделов дисциплины «Основы автоматики и САУ». При одновременных лекционном и лабораторном курсах рекомендуется лабораторный цикл начать с выполнения первых 4-х работ. Последовательность выполнения работ этого цикла может быть любой. Остальные 4 работы рекомендуются к исполнению при наличии достаточной лекционной поддержки. В случае модернизации лаб.работ (отмечены *) с использованием нового оборудования к описанию добавляются приложения (см. в конце пособия). При выполнении лаб.работы 2 уточнить вариант представленного макета.

Исследование простейшей САУ - физическая модель

(лабораторная работа 1)*

Цель работы:

1) экспериментальное определение показателей качества САУ и

установление их связи со структурой и параметрами САУ;

2) приобретение навыков работы с ЛХ.

Описание лабораторной установки

Лабораторная установка состоит из физической модели САУ, генератора сигналов и осциллографа и позволяет исследовать переходные и частотные характеристики системы. Физическая модель САУ включает в себя неизменную часть: амплитудный дискриминатор (вычитающий элемент), электронный интегратор (усилитель с частотнозависимой отрицательной обратной связью) и

изменяемую часть: четырехполюсник, структура которого задается с помощью переключателя, а параметры изменяются переменным резистором.

Передаточная функция электронного интегратора содержит усилительное звено и апериодическое звено, однако при большом коэффициенте усиления и исследовании САУ вблизи частоты среза ω_СР допускается аппроксимация передаточной функции электронного интегратора вида: К/jω, где значение коэффициента К определяется параметрами частотнозависимой обратной связи.

В результате имеется возможность исследования 4-х типов САУ с передаточными функциями в разомкнутом состоянии:

, , , .

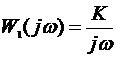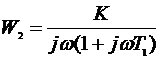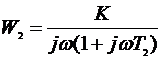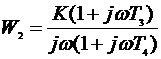Переходные характеристики наблюдаются на экране осциллографа при подаче на вход системы ступенчатого воздействия путем нажатия кнопки на макете (и ее удержании в нажатом состоянии в течение необходимого для наблюдения времени). Частотные характеристики исследуются при подаче на вход САУ сигнала от генератора. Частота сигнала устанавливается по шкале генератора, а амплитудные и фазовые соотношения исследуемых сигналов регистрируются по шкалам осциллографа.

Задание по работе

Для всех 4-х типов САУ (первые три типа САУ задаются переключателем при нулевом значении переменного резистора, 4-й тип САУ соответствует 3-й позиции переключателя при отличном от нуля значении переменного резистора) провести следующие расчеты и эксперименты.

1. Зарисовать схему лабораторной установки и записать номиналы ее элементов.

2. Построить асимптотические ЛХ для всех 4-х типов САУ (параметры передаточных функций должны соответствовать схеме, изображенной на макете). ЛХ всех САУ должны быть построены в одних координатных осях. С помощью ЛХ определить значения частоты среза ω_СР и запаса устойчивости по фазе γ и по ним воспроизвести осциллограммы переходных процессов.

3. Записать характеристические уравнения САУ и построить распределения полюсов передаточных функций замкнутых систем на плоскости комплексной переменной.

4. Посмотреть на осциллографе и зарисовать экспериментальные переходные процессы, сопоставив их с расчетными.

5. Экспериментально определить значения ω_СР и γ. Для этого изменять частоту гармонического входного сигнала до ω_СР , при которой модуль передаточной функции разомкнутой системы равен единице;

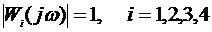. Значение f_СР ( ω_CР=2π f_СР ) фиксируется при равенстве амплитуд входного и выходного напряжений разомкнутой системы (гнезда e и y на макете). Величина γ фиксируется при частоте ω_CР по относительному смещению осциллограмм указанных напряжений (для САУ 1-го типа величина γ априори известна и она может использоваться в качестве «контрольной точки» эксперимента).

6. Снять экспериментальные амплитудно-частотные характеристики (АЧХ) замкнутых САУ, фиксируя отношение амплитуд выходного и входного напряжений (гнезда y и g на макете). Частоту входного гармонического сигнала изменять от минимально возможного (близкого к нулю) значения до значений, при которых модуль функции передачи замкнутых САУ падает до уровня 0,1 (количество экспериментальных точек определяется ресурсом времени выполнения лабораторной работы). Обязательно обратить внимание и зафиксировать резонансные явления. Построить графики АЧХ в одних осях (для оси частот использовать линейный масштаб).

7. Сопоставить расчетные и экспериментальные данные и сделать заключение о

- соотношениях, связывающих время нарастания t_Н, перерегулирование σ% и степень колебательности μ переходных процессов от параметров ω_CР и γ;

- связи ЛХ и переходных процессов с АЧХ САУ;

- связи переходных процессов с распределением полюсов передаточной функции замкнутых САУ.

Содержание отчета

1. Схема лабораторной установки с указанием номиналов ее элементов.

2. Функции передачи всех исследуемых систем в разомкнутом состоянии с указанием параметров.

3. Семейство ЛХ.

4. Распределения полюсов передаточных функций замкнутых САУ.

5. Семейство расчетных и экспериментальных переходных процессов.

6. Семейство АЧХ.

7. Расчетные соотношения для построения переходных процессов по ЛХ и рекомендации относительно их достоверности.

8. Выводы по результатам выполнения лабораторной работы.

1.4. Контрольные вопросы

1. Как изменятся переходные процессы и АЧХ САУ при увеличении (уменьшении) коэффициента К?

2. Как изменятся переходные процессы и АЧХ САУ при изменении постоянных времени T₁…T₄?

3. Каким образом влияет переменный резистор на переходные процессы САУ 4-го типа?

4. Какая связь существует между ЛХ и АЧХ?

5. В каком направлении следует изменять ЛХ и АЧХ для снижения колебательности системы?

6. Указать установившееся значение выходного напряжения САУ при g(t)=1(t) (ответ обосновать).

Задание по работе

1. Выполнить исследование системы ФАПЧ первого порядка астатизма. Для этого следует

1) снять экспериментальную зависимость 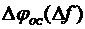; для построения графика 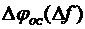требуется 3-5 точек при расстройке частоты в одну сторону и столько же точек – в другую; результаты свести в таблицу и построить график;

2) на графике 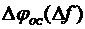выявить линейный участок, для которого рассчитать экспериментальное значение 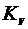; результат согласовать с преподавателем;

3) используя найденное значение 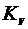, построить асимптотические ЛХ для 3-х вариантов включения системы ФАПЧ первого порядка астатизма (все ЛХ построить на одном графике для удобства сравнения);

4) оценить качество переходных процессов для всех 3-х вариантов системы; зарисовать схемы корректирующих цепей и указать быстродействие и степень колебательности переходных процессов в системе ФАПЧ при включении этих цепей;

5) сопоставить расчетные (построенные с помощью ЛХ) и экспериментальные характеристики переходных процессов.

2. Выполнить исследование системы ФАПЧ второго порядка астатизма. Для этого следует

1) при выключенном двигателе вручную установить ротор конденсатора переменной емкости в среднее положение;

2) выполнить грубое сведение частот генераторов и обеспечить ввод системы в режим слежения (без цепей последовательной коррекции);

3) включить двигатель и плавно изменяя частоту внешнего генератора ручкой «Расстройка» убедиться

- в наличии реакции конденсатора переменной емкости на изменении частоты генератора;

- в отсутствии ошибки слежения при постоянной расстройке частоты генератора (по фигуре Лиссажу);

- в наличии ошибки слежения при изменении частоты генератора (при повороте ручки генератора «Расстройка»);

4) изобразить структурную схему формирующего фильтра для ситуации Δf=const и объяснить причины изменения свойств системы ФАПЧ при включении двигателя.

Содержание отчета

1. Функциональная схема системы ФАПЧ (первого и второго порядка астатизма), схемы корректирующих элементов с указанием номиналов резисторов и емкостей, функции передачи разомкнутой системы для всех исследуемых вариантов.

2. Таблица и график зависимости 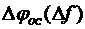, расчет 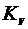и постоянных времени корректирующих элементов.

3. Асимптотические ЛХ для 3-х вариантов построения системы ФАПЧ первого порядка астатизма.

4. Сравнительные характеристики переходных процессов и их объяснение.

5. Структура формирующего фильтра для ситуации Δf=const и объяснение эффектов синхронности (равенства частот) и синфазности ( 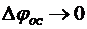) входного и выходного сигналов системы ФАПЧ второго порядка астатизма.

2.4. Контрольные вопросы

1. Как работают функциональные элементы системы ФАПЧ и вся система в целом?

2. Какой параметр входного сигнала является информативным для системы ФАПЧ?

3. Какой вид имеет структура формирующего фильтра в случае Δf(t)=0, Δf(t)=const, Δf(t)=vt? Какой вид имеет структура согласованной САУ?

4. Как изменяются свойства системы ФАПЧ при увеличении (уменьшении) коэффициента усиления ?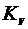

5. С какой целью включаются корректирующие элементы в системе ФАПЧ первого порядка астатизма?

6. Как изменяются свойства системы ФАПЧ при увеличении порядка астатизма?

7. Что произойдет с системой ФАПЧ, если при включенном двигателе отключить реактивный элемент?

Задание по работе

1. Включить генератор, макет и осциллограф.

2. Разомкнуть систему ФАПЧ (переключатель в положении 1).

3. Настроить осциллограф для наблюдения фигур Лиссажу.

4. Изменяя частоту генератора, обеспечить совпадение частот внешнего генератора и управляемого генератора системы ФАПЧ (эллипс на экране осциллографа). Замкнуть систему ФАПЧ (переключатель в положении 2). Измерить полосу удержания системы ФАПЧ.

5. Ручку «частота генератора» установить в среднее положение (см.п.4). С помощью фазовращателя зафиксировать положение эллипса, представив его в виде линии или «восьмерки». Изменяя частоту генератора 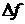(ручка «расстройка»), и измеряя приращение фазового сдвига 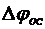с помощью фазовращателя, построить зависимость 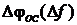(должна получиться нечетная функция). Для построения графика 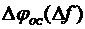требуется 3-5 точек при расстройке частоты в одну сторону и столько же точек – в другую.

6. Для линейного участка зависимости 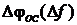определить коэффициент усиления 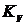с помощью формулы (1). Это значение согласовать с преподавателем.

7. Используя полученное значение 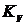, построить построить асимптотические логарифмические характеристики для 3-х вариантов включения системы ФАПЧ первого порядка астатизма (все ЛХ построить на одном графике для удобства сравнения; параметры корректирующих элементов указаны на макете). По логарифмическим характеристикам оценить качество переходных процессов.

8. Качественно оценить переходные процессы в системе ФАПЧ (для этой цели используется тумблер «скачок фазы»).

9. Включить «эквивалент двигателя» и повторить пп.4-6 (при изменении частоты генератора учесть длительный перезаряд емкости электронного интегратора). Схему электронного интегратора зарисовать и вычислить его передаточную функцию (в общем виде).

Содержание отчета

1. Функциональная схема системы ФАПЧ, схемы корректирующих элементов с указанием номиналов резисторов и емкостей, схема электронного интегратора, функции передачи разомкнутой системы для всех исследуемых вариантов.

2. Таблица и график зависимости 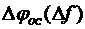, расчет 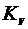и постоянных времени корректирующих элементов.

3. Асимптотические ЛХ для 3-х вариантов построения системы ФАПЧ первого порядка астатизма.

4. Сравнительные характеристики переходных процессов и их объяснение.

5. Полосы удержания исследуемых систем ФАПЧ.

6. Структура формирующего фильтра для ситуации Δf=const.

3.4. Контрольные вопросы

1. Как работают функциональные элементы системы ФАПЧ и вся система в целом?

2. Какой параметр входного сигнала является информативным для системы ФАПЧ?

3. Какой вид имеет структура формирующего фильтра в случае Δf(t)=0, Δf(t)=const, Δf(t)=vt? Какой вид имеет структура согласованной САУ?

4. Как изменяются свойства системы ФАПЧ при увеличении (уменьшении) коэффициента усиления ?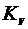

5. С какой целью включаются корректирующие элементы в системе ФАПЧ первого порядка астатизма?

6. Как изменяются свойства системы ФАПЧ при электронного интегратора?

Задание по работе

1. Снять зависимость угловой скорости вращения вала двигателя от входного напряжения U_ВХ при выключенной обратной связи (измерение угловой скорости вращения вала двигателя выполняется путем измерения напряжения на выходе тахогенератора). Измерить величину зоны нечувствительности характеристики двигателя.

2. Снять зависимость угловой скорости вращения вала двигателя от входного напряжения U_ВХ при включенной обратной связи. Измерить величину зоны нечувствительности характеристики привода.

3. Объяснить эффекты, связанные с уменьшением зоны нечувствительности и линеаризацией характеристики привода.

4. С помощью осциллографа при скачкообразном включении напряжения U_ВХ определить постоянную времени двигателя 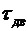(без обратной связи), полагая , что переходный процесс завершается за время, примерно равное 3 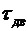. Так как реальный двигатель является нелинейным устройством, величина 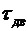определяется при средних скоростях вращения вала.

5. Определить постоянную времени привода с тахометрической обратной связью .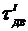

6. Вычислить коэффициент усиления двигателя 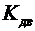[рад*с^-1]. Для этого, по данным п.1 задания определить крутизну зависимости 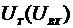на средних скоростях вращения вала двигателя и результат разделить на коэффициент усиления тахогенератора, равный 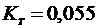[в*рад^-1*с]. Используя вычисленное значение 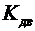и экспериментально полученное значение 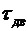, построить ЛХ для функции передачи двигателя.

7. В соответствии с функцией передачи 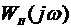построить ЛХ для привода с тахометрической обратной связью (на том же графике).

8. По данным пп.1 и 2 задания определить коэффициент усиления 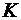усилителя, как отношение зон нечувствительности характеристик двигателя с выключенной и включенной обратной связи. Сопоставить полученное значение с величиной 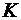, указанной на макете. Выполнить построение ЛАЧХ, аналогичных графикам рис.2. Сравнить найденное графическим способом 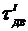с экспериментальным значением в п.5 (расхождения объяснить).

Содержание отчета

1. Функциональная и структурная схемы привода с тахометрической обратной связью.

2. Зависимости угловой скорости вращения вала привода от входного напряжения при включенной и выключенной обратной связи.

3. Значения коэффициента усиления 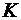(экспериментальное и теоретическое).

4. Значения постоянных времени привода при включенной и выключенной обратной связи.

5. Расчет коэффициента усиления двигателя.

6. ЛХ двигателя и привода с тахометрической обратной связью.

7. Семейство ЛАЧХ для графического способа определения величины .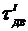

4.4. Контрольные вопросы

1. Какую функцию передачи имеет двигатель, если выходной величиной является угловая скорость вращения его вала?

2. Какую функцию передачи имеет двигатель, если выходной величиной является угол поворота его вала?

3. Какие элементы схемы привода обеспечивают уменьшение зоны нечувствительности?

4. Какие элементы схемы привода обеспечивают снижение постоянной времени?

5. Обосновать эффект линеаризации статической характеристики привода.

6. Как построить ЛАЧХ замкнутой системы, если известна ЛАЧХ цепей прямой и обратной связей?

7. Почему переходный процесс в приводе с тахометрической обратной связью не имеет перерегулирования?

Задание по работе

1). Включить лабораторную установку и осциллограф. Листая страницы мультиметра (кнопки << и >>), ознакомиться с их содержанием.

2). В соответствии с приведенным выше описанием синтезатора частоты изобразить его функциональную схему.

3). Убедиться в работоспособности синтезатора частоты. Для этого включить систему ФАПЧ, ИФД1, установить частоту выходного сигнала 1050 кГц и К_ФД=4,5.

Полосу пропускания ФНЧ выбрать равной 1 кГц, род работы – немодулированные колебания. Изменяя частоту выходного сигнала через 10 кГц до 1250 кГц наблюдать показание мультиметра F_r, а на экране осциллографа – напряжение на выходе ИФД1. Изменить частоту еще на 10 кГц (индикатор УСТАНОВКА ЧАСТОТЫ покажет 1000 кГц) и зарисовать осциллограмму биений на выходе ИФД1 при срыве слежения, объяснить ее форму.

4). Снять настроечную характеристику управляемого генератора. Для этого убедиться в установке переключателя РОД РАБОТЫ в положении НЕМОД., систему ФАПЧ выключить. Изменяя управляющее напряжение на варикапе ручкой К_ФД от минимального до максимального значений, снять зависимость частоты выходного сигнала F_r от напряжения (значения F_r и u_фд фиксировать по показаниям мультиметра; убедиться, что показания осциллографа соответствуют значениям u_фд). Построить график и определить на нем линейный участок. В центре линейного участка выбрать рабочую частоту.

5). Исследовать переходные процессы в системе ФАПЧ. Для этого включить систему ФАПЧ с ИФД1 на выбранной рабочей частоте, установить режим 2-уровневой частотной телеграфии (переключатель РОД РАБОТЫ в положение ЧТ1). Полосу пропускания ФНЧ выбрать равной 1 кГц. Записать значение выбранной рабочей частоты. Увеличить усиление осциллографа и наблюдать на его экране переходные процессы на выходе ИФД, зарисовать их при нескольких значениях К_ФД (не допуская срыва слежения).

Установить ручку К_ФД в положение, соответствующее коэффициенту усиления дискретной системы К=К_vΔt=1 (режим максимального быстродействия, разделяющий монотонные и колебательные переходные процессы). Положив К_v=1/Δt=1000, зафиксировать значение К_ФД. Уменьшить значение К_ФД так, чтобы соблюдалось условие теоремы Котельникова (t_н>>Δt). Измерить время нарастания переходного процесса t_н (одной ступеньке соответствует 1 мсек) и зафиксировать новое значение К_ФД. Уменьшить прежнее значение К_v во столько раз, во сколько уменьшилось К_ФД. Построить логарифмические характеристики эквивалентной непрерывной системы ФАПЧ для уменьшенного значения К_v. Определить частоту среза и по ней определить время нарастания переходного процесса. Сопоставить результат с экспериментальным значением.

6). Оценить влияние К_ДПКД на переходные процессы системы ФАПЧ. Для этого следует, не меняя положения ручки К_ФД, увеличивать частоту выходного сигнала через 10 кГц, наблюдая за формой переходного процесса. Характерные осциллограммы зарисовать.

7). Оценить влияние ФНЧ на переходные процессы системы ФАПЧ. Для этого установить полосу пропускания ФНЧ равной 50 Гц и, изменяя К_ФД, наблюдать за формой переходного процесса. Характерные осциллограммы зарисовать.

Содержание отчета

1. Функциональная схема синтезатора частоты (см. п.2 Задания).

2. Условия и результаты эксперимента по п.3 Задания, в т.ч.:

- значения F_r и u_ФД;

- осциллограммы биений на выходе ИФД1.

3. Настроечная характеристика управляемого генератора с указанием линейного участка и рабочей частоты.

4. Условия и результаты эксперимента по п.5 Задания, в т.ч.:

- значение F_r;

- осциллограммы переходных процессов для нескольких значений К_ФД;

- осциллограммы переходных процессов в режиме максимального быстродействия системы;

- осциллограммы переходного процесса, соответствующего условию t_н>>Δt;

- значение К_v;

- асимптотические логарифмические характеристики системы ФАПЧ с указанием частоты среза;

- сопоставление экспериментального и расчетного значений времени нарастания переходного процесса.

5. Характерные переходные процессы, иллюстрирующие влияние К_ДПКД (см. п.6 Задания).

6. Характерные переходные процессы, иллюстрирующие влияние ФНЧ (см. п.7 Задания).

5.4. Контрольные вопросы

1. В чем заключаются особенности системы ФАПЧ, работающей в составе синтезатора частоты?

2. Как влияет делитель с переменным коэффициентом деления на показатели качества системы ФАПЧ?

3. Как меняется форма биений на выходе ИФД1 при захвате частоты?

4. Какими средствами обеспечивается увеличение полосы удержания системы ФАПЧ?

5. Записать разностное уравнение дискретной системы 1-го порядка и указать область допустимых значений для коэффициента усиления.

6. Объяснить влияние ФНЧ на качество переходных процессов системы ФАПЧ.

Задание по работе

1. В отсутствии случайного процесса v(t) экспериментально исследовать и зарисовать переходные процессы в САУ всех 3-х типов. Для САУ 3-го типа исследование провести при нескольких значениях переменного резистора.

2. Построить семейство ЛХ исследуемых САУ (если параметры схемы лабораторного макета неизвестны, построения можно выполнить качественно, однако они не должны противоречить результатам п.1 задания).

3. В присутствии случайного процесса v(t) экспериментально исследовать зависимость σ_Ш от структуры и параметров САУ (в процессе измерения σ_Ш следует усреднять показания вольтметра за интервал времени 1-3 минуты). В процессе исследований сопоставить σ_Ш для САУ 1-го и 2-го типов. Для САУ 3-го типа следует, изменяя значение переменного резистора, убедиться в наличии минимума σ_Ш.

Зависимость σ_Ш от значения переменного резистора зарисовать.

4. Повторить п.1 для оптимальных параметров САУ 3-го типа.

5. Построить АЧХ САУ 3-го типа для 3-х значений переменного резистора, включая оптимальное.

Содержание отчета

1. Функциональная схема лабораторного макета.

2. Функции передачи исследуемых САУ.

3. Результаты экспериментальных исследований переходных процессов САУ.

4. ЛХ исследуемых САУ.

5. Результаты экспериментальных исследований зависимости σ_Ш от структуры и параметров САУ.

6. Семейство АЧХ для САУ 3-го типа.

6.4. Контрольные вопросы

1. Объяснить поведение σ_Ш в САУ 1-го и 2-го типов.

2. Объяснить поведение σ_Ш в САУ 3-го типа.

3. Объяснить поведение σ_Ш в САУ 3-го типа при неограниченном росте значения переменного резистора.

4. Дать геометрическую и физическую интерпретацию эффективной полосы САУ.

5. Каков закон распределения вероятностей процесса на выходе САУ, если на входе он гауссовский?

6. Изобразить (качественно) закон распределения вероятностей случайного процесса на выходе измерителя среднеквадратического значения шумовой ошибки.

7. Параметрическая оптимизация САУ при наличии динамической и шумовой ошибок(лабораторная работа 6)*

Цель работы – практическое изучение возможности параметрической оптимизации САУ в установившемся режиме по критерию минимума среднего квадрата суммарной ошибки.

Задание по работе

1. Снять экспериментальные зависимости σ_g и σ_ФЛ от параметра САУ K (для функции передачи электронного интегратора использовать аппроксимацию вида K/jω, где K определяется параметрами частотно-зависимой обратной связи операционного усилителя).

2. Снять экспериментальную зависимость σ_Σ от параметра САУ K и определить значение K_ОПТ.

3. Построить графики всех зависимостей в одних координатных осях.

4. Привести расчетные соотношения и результаты вычислений значения K_ОПТ двумя способами.

5. Сопоставить результаты эксперимента с теоретическими сведениями. Подтвердить наличие корреляции процессов g(t) и v(t).

6. Построить семейство ЛХ и АЧХ САУ для нескольких значений параметра K (в том числе – для расчетного значения K_ОПТ).

Содержание отчета

1. Структурная схема исследуемой САУ.

2. Основные расчетные соотношения.

3. Экспериментальные зависимости по пп.1-4 задания.

4. Семейства ЛХ и АЧХ.

5. Выводы по результатам экспериментальных исследований.

7.4. Контрольные вопросы

1. С физической точки зрения объяснить влияние параметра K на уровень флюктуационной и динамической составляющих ошибки САУ.

2. Как вычисляется дисперсия суммы 2-х коррелированных случайных процессов?

3. Какой порядок астатизма имеет исследуемая система (рис.3) по выходу y(t)? по выходу ε(t)?

4. Оценить влияние параметра K на дисперсию случайного процесса y(t), если на вход САУ поступает только экспоненциально-коррелированный процесс g(t). Чему равна дисперсия y(t) при неограниченном росте K?

5. Как отражается улучшение фильтрующих свойств системы на корреляционных свойствах флюктуационной ошибки?

6. Какой должна быть структура САУ, согласованной с формирующим фильтром данного макета?

Исследование нелинейной САУ

(лабораторная работа 7)*

Цель работы – ознакомление с практическим использованием методов гармонической и статистической линеаризации при анализе САУ, содержащей релейный элемент и инерционную линейную часть.

Задание по работе

1. Расчетная часть.

1) Построить ЛХ линейных САУ с различными цепями коррекции (значения параметров линейной части САУ указаны на лабораторном макете).

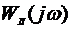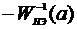2) Построить годографы и нелинейных САУ с различными цепями коррекции и выполнить анализ автоколебаний. При построении годографа 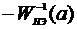следует учесть, что

,

.

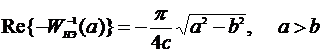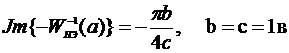3) Для различных значений 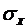построить семейство ЛХ линеаризованных САУ с различными цепями коррекции и функцией передачи 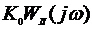. При вычислении коэффициента 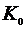использовать допущение 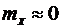(ошибка слежения в среднем близка к нулю), при котором громоздкое выражение для 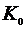можно упростить:

.

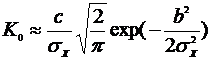Расчет 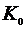выполнить для значений 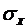, равных .

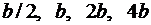2. Экспериментальная часть.

1) Подавая скачкообразное воздействие g(t), посмотреть на экране осциллографа и зарисовать переходные процессы линейных САУ 3-х типов (без коррекции и с цепями коррекции z₁(jω) и z₂(jω)). По степени колебательности переходных процессов оценить запас устойчивости по фазе.

2) Выполнить экспериментальный анализ автоколебаний в нелинейных САУ 3-х типов. Измерить частоту и амплитуду автоколебаний.

3) Для 3-х типов нелинейных САУ экспериментально исследовать срыв автоколебаний при изменении уровня шума на входе системы. Для этого следует постепенно увеличивать уровень шума до некоторого порогового уровня, при котором исчезает регулярная составляющая в выходном сигнале САУ (отсутствие регулярных автоколебаний свидетельствует о выполнении условий статистической линеаризации САУ). Пороговый уровень шума измерить.

4) Экспериментально исследовать влияние уровня шума на качество переходных процессов нелинейных САУ 3-х типов. Для этого установить уровень шума, соответствующий линеаризации САУ (срыв автоколебаний) и посмотреть несколько переходных процессов на экране осциллографа. Зарисовать усредненный (по ансамблю реализаций) переходный процесс. Затем увеличить уровень шума, снова посмотреть несколько реализаций переходного процесса, зарисовать усредненный процесс и сопоставить результаты. Уровни шума измерить с помощью осциллографа (при оценке 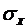процесс считать нормальным, не выходящим за пределы ).

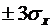5) Экспериментально оценить фильтрующие свойства линейных и нелинейных САУ 3-х типов.

Содержание отчета

1. Структурная схема макета САУ.

2. ЛХ линейных САУ 3-х типов.

3. Годографы для анализа автоколебаний в нелинейных САУ 3-х типов.

4. Семейства ЛХ линеаризованных САУ.

5. Осциллограммы переходных процессов линейных САУ 3-х типов.

6. Результаты экспериментального анализа автоколебаний в нелинейных САУ 3-х типов.

7. Значения пороговых уровней шума, при которых выполняются условия статистической линеаризации нелинейных САУ 3-х типов.

8. Усредненные переходные процессы для 2-х значений .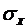

9. Оценки фильтрующих свойств всех САУ.

8.4. Контрольные вопросы

1. Как влияют цепи коррекции на переходные процессы линейных САУ?

2. Как определяются амплитуда и частота автоколебаний в нелинейных САУ?

3. Влияет ли уровень шума на качество переходных процессов в линейных САУ?

4. Влияет ли уровень шума на качество переходных процессов в нелинейных САУ?

5. Объяснить эффект срыва автоколебаний в нелинейной САУ при действии шума.

6. Как изменяется коэффициент 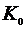при увеличении уровня шума и какие показатели качества линеаризованной САУ при этом меняются?

9. Исследование нелинейных элементов методом статистической линеаризации(лабораторная работа 8)

Цель работы – экспериментальная оценка статистических характеристик безынерционных нелинейных элементов, используемых в методе статистической линеаризации нелинейных САУ.

Задание по работе

1. Ознакомиться с лабораторным макетом и представленной на нем схемой измерений. Схему экспериментальных исследований и статические характеристики y(x) нелинейных элементов зарисовать.

2. Снять экспериментальные характеристик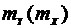и и 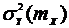при нескольких значениях уровня шума 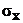(уровень шума отсчитывается в условных значениях по шкале потенциометра).

3. Для каждого нелинейного элемента построить 2 семейства графиков: 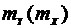и 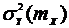при выбранных значениях уровня шума .

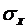4. С физических позиций дать объяснение полученным результатам. Для этого следует рассмотреть прохождение через нелинейный элемент нормального случайного процесса с заданными параметрам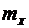и и 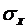и оперировать плотностью распределения вероятностей W(y).

5. Используя полученные в результате эксперимента зависимости 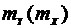, определить 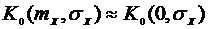и построить зависимости .

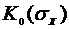9.3. Контрольные вопросы

1. Каким образом параметры 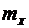и 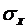влияют на вид функции W(y)?

2. Дать физическую трактовку зависимосте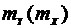й и .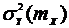

3. Как влияет уровень шума на входе нелинейного элемента на показатели качества нелинейной САУ?

4. Перечислить ограничения применимости метода статистической линеаризации.

Список литературы

1. Коновалов Г.Ф. Радиоавтоматика. Учеб.для вузов по спец.Радиотехника, -

М. Высш.шк. 2003. - 335с.

2. Первачев С.В. Радиоавтоматика. Учеб.для вузов, - М.- Радио и связь - 1982. - 296с.

3. Радиоавтоматика. Учеб.пособие для студ.вузов спец.Радиотехника /

В.А.Бесекерский, А.А.Елисеев, А.В.Небылов и др. Под ред.В.А.Бесекерского, - М.- Высш.шк., 1985. - 271с.

4. Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. - М.: Наука, 1972. - 768 с.

5. Воронов А. А. Основы теории автоматического управления. - М.: Энергия. - Т. 1. - 1980. - 312 с.; Т. 2. - 1981. - 304 с.

6. Красовский А. А., Поспелов Г. С. Основы автоматики и технической кибернетики. - М.: ГЭИ, 1962. - 600 с.

7. Первачев С. В., Валуев А. А., Чиликин В. М. Статистическая динамика радиотехнических следящих систем. М.: Сов. радио, 1973. – 488 с.

8. Теория автоматического управления: В 2 ч. / Под ред. А. А. Воронова. - М.: Высш. шк., 1986. - Ч. 1 - 2. - 655 с.

9. Теорiя автоматичного управлiння / Г. Ф. Зайцев, В. К. Стеклов, О. I. Брiцький; За ред. проф. Г. Ф. Зайцева. – К.: Технiка, 2002. – 688 с.

10. Юревич Е. И. Теория автоматического управления. - Л.: Энергия. Ленингр. отд-ние, 1975. - 410 с.

Содержание

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1. Исследование простейшей САУ - физическая модель

(лабораторная работа 1) . . . . . . . . . . . . . . . . . . . . . . 3

2. Исследование системы фазовой автоподстройки частоты (ФАПЧ)

(лабораторная работа 2, макет с двигат<