Метод подстановки в неопределенном интеграле

Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных приемов является метод подстановки или замены переменной интегрирования. Сущность этого метода заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому интегралу, который сравнительно легко берется непосредственно. Если после замены переменной интеграл стал проще, то цель подстановки достигнута. В основе интегрирования методом подстановки лежит формула

Алгоритм вычисления неопределенного интеграла методом подстановки:

1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).

2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.

3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.

4. Производят замену под интегралом.

5. Находят полученный интеграл.

6. В результате производят обратную замену, т.е. переходят к старой переменной.

7. Результат полезно проверять дифференцированием.

Задание:Найти неопределённые интегралы

1. .

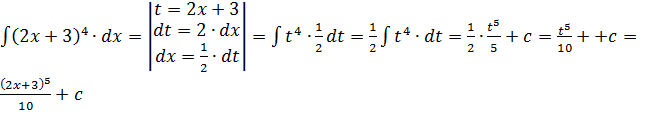Проверка:

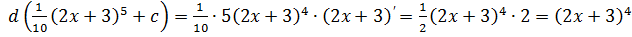, что совпадает с подынтегральной функцией, следовательно, интеграл найден верно.

2.

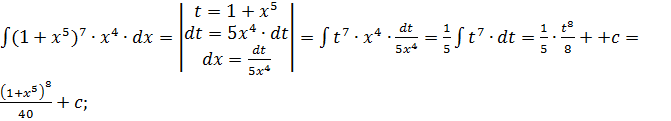
3.

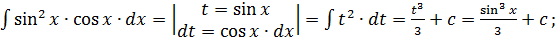
4.Предварительно преобразуем подынтегральную функцию в сложную степенную функцию, а затем применим метод подстановки в неопределённом интеграле:

;

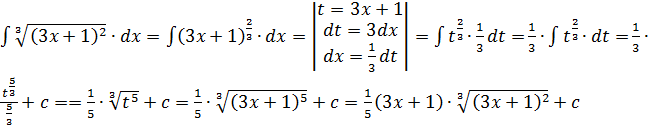5.

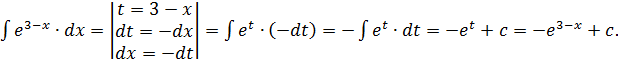
6.

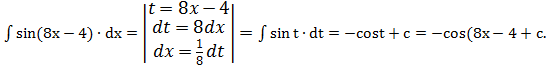
Наибольшую трудность при практическом применении метода подстановки вызывает правильность определения, к какому табличному интегралу удастся привести заданный интеграл.

Рассмотрим типовые варианты. В Таблице 1 приведены варианты правильных подстановок в различных типах неопределенных интегралов и те интегралы, к которым удаётся прийти в результате подстановки.

Таблица 1

№ п/п	Интеграл	Табличный интеграл, к которому будет приведен данный интеграл	Замена переменной
1.		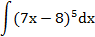	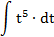t = 7x-8
2.		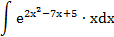	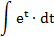t = 2x2-7x+5
3.		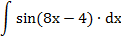	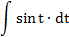t = 8x-4
4.		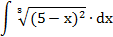	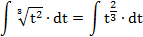t = 5-x
5.		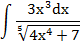	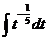t = 4x4+7
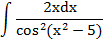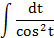			t = x2-5
7.		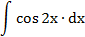	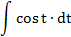t = 2x
8.		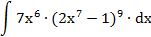	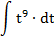t = 2x7-1

Методические указания и примеры типового расчёта

Практической работы №11 по теме

«Геометрические тела. Вычисление объёмов и площадей поверхности многогранников и тел вращения»

Теория

Параллелепипедом называется призма, в основании которой лежит параллелограмм.

Виды параллелепипедов:

1) Прямой 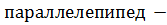это такой параллелепипед, у которого боковые рёбра перпендикулярны плоскостям основания. (У него все боковые грани являются прямоугольниками, а основания 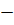параллелограммами).

2) Прямоугольный параллелепипед 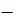это прямой параллелепипед, но в основании которого лежит прямоугольник. (У него все грани являются прямоугольниками).

3) Куб 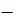это прямоугольный параллелепипед у которого три ребра, выходящие из одной вершины, равны. (У куба все грани 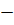равные квадраты).

Диагональное сечение призмы это пересечение призмы с диагональной плоскостью. У прямоугольного параллелепипеда диагональное сечение это прямоугольник, одна из сторон которого равна диагонали прямоугольника, лежащего в основании, а вторая сторона является боковым ребром параллелепипеда.

Пирамидой называется многогранник, в основании которого лежит произвольный многоугольник, а остальные грани являются треугольниками с общей вершиной.

Виды пирамид:

1)Треугольная, четырёхугольная, пятиугольная,...-в зависимости от многоугольника. лежащего в основании пирамиды;

2) Правильная и неправильная пирамида.

Пирамида называется правильной, если в её основании лежит правильный многоугольник и вершина пирамиды проектируется в центр основания.

Апофемой называется высота боковой грани правильной пирамиды, опущенная из её вершины (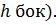

Основные формулы

Куб: 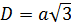-диагональ куба, ребро которого равно ;

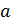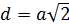-диагональ квадрата со стороной ;

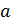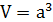-объём куба.

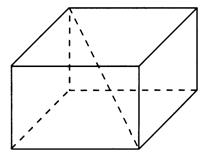
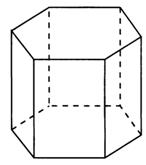
Призма: ,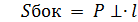

где 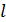длина бокового ребра - периметр перпендикулярного сечения;

Sполн. призм. = Sбок + 2 Sоснов;

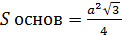-площадь основания правильной треугольной призмы;

V_призмы = S_основ ·H, где Н- высота призмы, если призма прямая, то её высотой является боковое ребро ;

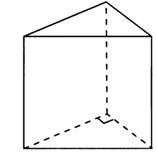
Пирамида:

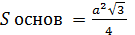- площадь основания правильной треугольной пирамиды;

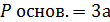- периметр основания правильной треугольной пирамиды;

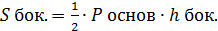- площадь боковой поверхности правильной пирамиды;

Усечённая пирамида:

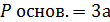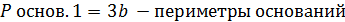; _, где 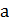и b- стороны оснований;

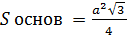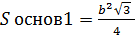; - площади оснований правильной треугольной усечённой пирамиды;

;

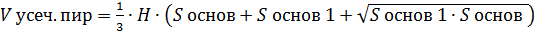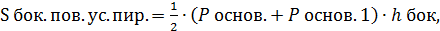где 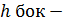апофема усечённой пирамиды;

.

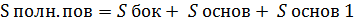Тела вращения

Цилиндр:

; ;

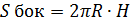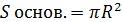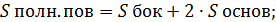
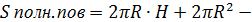площадь полной поверхности цилиндра;

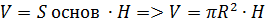- объём цилиндра;

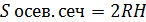-площадь осевого сечения цилиндра;

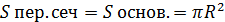-площадь перпендикулярного сечения цилиндра.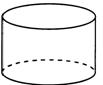

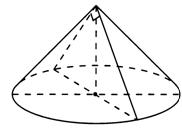
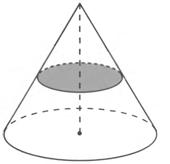
Конус:

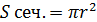-площадь перпендикулярного сечения конуса, r-радиус круга в сечении;

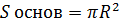- площадь основания конуса;

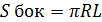- площадь боковой поверхности конуса;

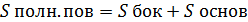- площадь полной поверхности конуса;

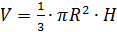- объём конуса, H- высота конуса.

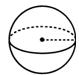
Шар:

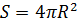- площадь поверхности шара; R- радиус шара;

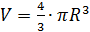- объём шара;

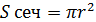-площадь сечения шара плоскостью, отстоящей от центра шара на расстояние d; 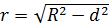- радиус круга в сечении;

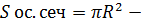площадь осевого сечения шара.

Вписанные и описанные многогранники и тела вращения:

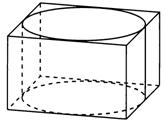
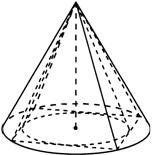
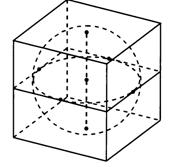
Рис.1 Рис.2 Рис.3

Рис.1 - Правильная четырёхугольная призма, описанная вокруг цилиндра;

Рис.2- Конус, описанный вокруг правильной четырёхугольной пирамиды, в которую вписан второй конус;

Рис.3- Прямоугольный параллелепипед, описанный вокруг сферы;

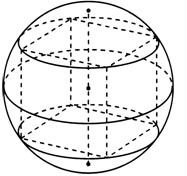
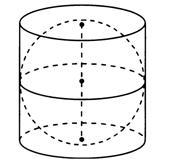
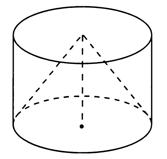
Рис.4 Рис.5 Рис.6

Рис.4- Куб, вписанный в шар;

Рис.5- Цилиндр, описанный вокруг шара

Рис.6-Конус, вписанный в цилиндр.

Задание 1. Найдите площадь многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.

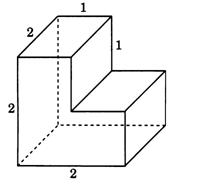
Решение

Поверхность многогранника состоит из двух квадратов со стороной 2, площадь каждого из которых равна 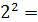4, четырёх прямоугольников со сторонами 1 и 2, площадь каждого из которых равна 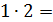2, и двух невыпуклых шестиугольников , площадь каждого из которых равна

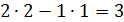. Значит, площадь поверхности многогранника равна сумме площадей указанных многоугольников: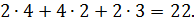

Ответ: 22

Задание 2.Найдите объём фигуры, изображённой на рисунке. Её основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых рёбер перпендикулярно плоскости основания и равно 3.

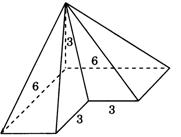
Решение

Данный многогранник представляет из себя четырёхугольную пирамиду, в основании которой лежит квадрат со стороной 6, из которой вырезана пирамида, в основании которой находится квадрат со стороной 3, а вершина совпадает с вершиной первой пирамиды. Высотой обеих пирамид является боковое ребро первой пирамиды, по условию, перпендикулярное плоскости основания пирамиды и равное 3. Объём пирамиды находится по формуле

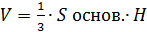, тогда получаем:

.

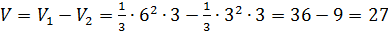Ответ:27

Задание 3. Радиусы двух шаров равны 6 и 8 см. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей данных шаров.

Решение

Площадь поверхности данных шаров равна

,

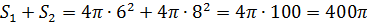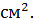
Радиус шара, площадь которого равна сумме площадей поверхностей данных шаров: 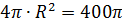, отсюда находим

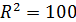, R= 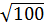=10 (см).

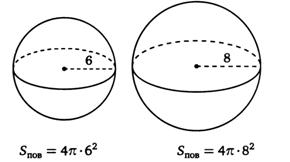
Ответ: 10 см

Задание 4.Если каждое ребро куба увеличить на 1, то площадь его поверхности увеличится на 30. Найдите ребро куба и его объём (Рис.1)

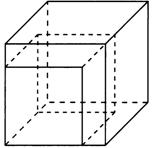
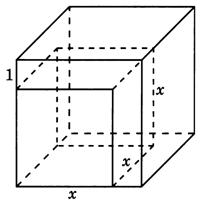
Рис.1 Рис.2

Решение

Обозначим ребро куба х (Рис.2). Шесть равных граней куба являются квадратами, поэтому площадь поверхности куба 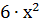. Если ребро куба увеличить на 1, то оно станет равно 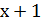, а площадь поверхности- 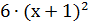. Учитывая, что площадь поверхности куба при этом увеличивается на 30, получаем уравнение

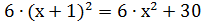, решая его находим х=2.

Ответ:2

Задание 5.В цилиндрический сосуд. в котором находится 6 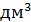воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза.

Чему равен объём детали?

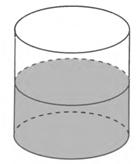
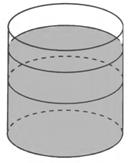
Решение

Так как уровень жидкости в сосуде поднялся в 1,5 раза, то и объём увеличился в 1,5 раза ( 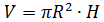), т.е. стал равен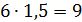 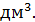Следовательно, объём детали равен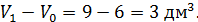

Ответ: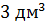

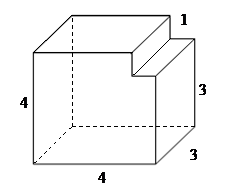Задание 6.Найти объем фигуры:

Решение:

Данный многогранник представляет из себя параллелепипед с объемом V₁, из которого удален меньший параллелепипед с объемом V₂.

, .

;

, ,

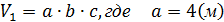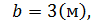
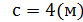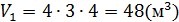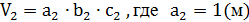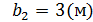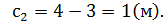
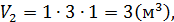тогда вычисляем

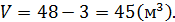
Ответ: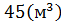

Задание 7.В прямоугольный параллелепипед вписан цилиндр, радиус основания и высота которого равны 5,5 см. Найти объем параллелепипеда и объем цилиндра.

Решение:

Т.к. в прямоугольный параллелепипед вписан цилиндр, то основанием параллелепипеда является квадрат.

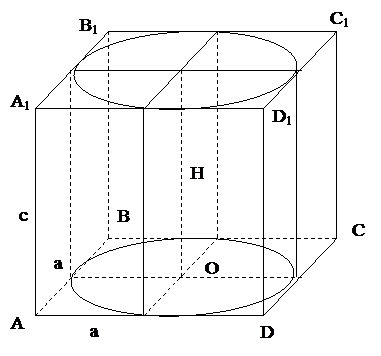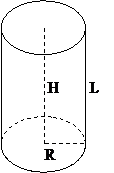Решение:

1. , .

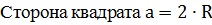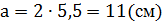2. Высота параллелепипеда равна высоте вписанного в него цилиндра:

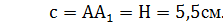
3. Объем прямоугольного параллелепипеда: 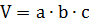, отсюда

.

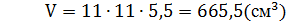4. Объем цилиндра: 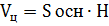, где ,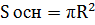

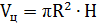, тогда вычисляем

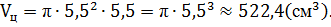
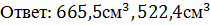
Задание 8.Из параллелепипеда (см. условие предыдущей задачи) был удален цилиндр, найти объем получившейся фигуры и площадь её полной поверхности.

Решение:

,

.

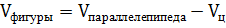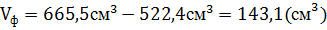Площадь полной поверхности этой фигуры:

,

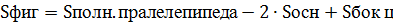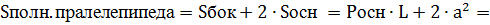
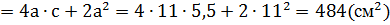
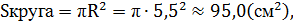
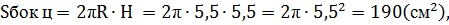
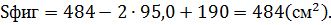
Ответ: , =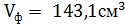

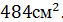
Задание 9.Найти объем и площадь полной поверхности фигуры, изображенной на рисунке :

Решение:

Объём многогранника равен сумме объёмов двух прямоугольных параллелепипедов: ,

;

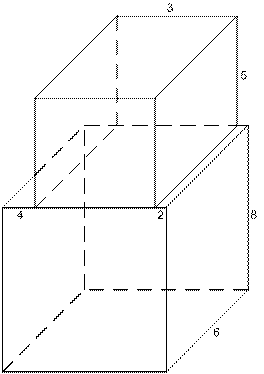
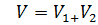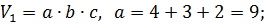
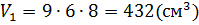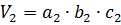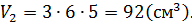, Тогда вычисляем

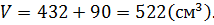
Площадь поверхности фигуры равна сумме площадей поверхности большого параллелепипеда и площади боковой поверхности маленького параллелепипеда:

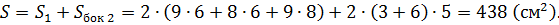
Ответ: 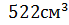, 438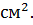

Задание №10.Найти площадь диагонального сечения правильной четырёхугольной призмы, высота которой равна 4 см., а длина стороны основания равна 10 см.

Дано: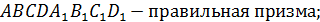

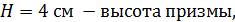
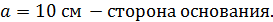
Найти: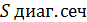

Решение:

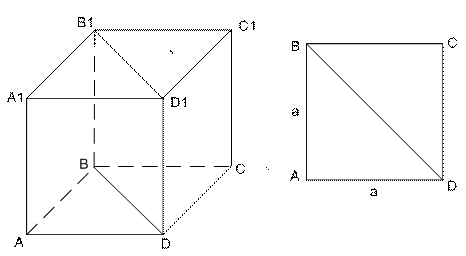
1) Призма правильная, поэтому она прямая, то есть её боковое ребро является высотой: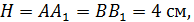

и в основании призмы лежит квадрат диагональ которого :

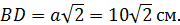
2) Диагональным сечением призмы является прямоугольник 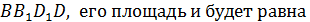площади диагонального сечения.

,

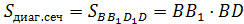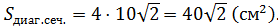
Ответ: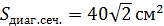

Задача № 11.Прямоугольный треугольник АВС вращается вокруг гипотенузы АВ. Найти объём тела вращения и площадь поверхности тела вращения, если известно угол 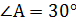, а противолежащий катет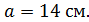

Дано: 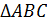, , 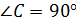, 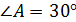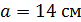- катет треугольника;

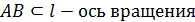
Найти: 1) V т.вр.; 2) S т.вр.

Решение:

1) Фигурой вращения является тело, состоящее из двух конусов с общим основанием.

Образующие конусов: L₁ = AC = b; L₂ = BC = a = 14 см.

Высоты конусов: Н₁ = АО; Н₂ = ВО

Радиус основания конусов: R = CO, где CO⊥AB.

2) Решим прямоугольный треугольник АВС: ;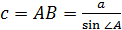

;

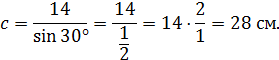
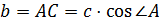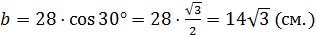
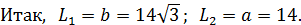
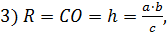
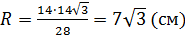. Итак,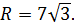

4) Объём тела вращения равен сумме объёмов двух конусов:

,

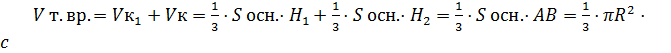учли, что 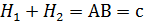-гипотенуза треугольника АВС.

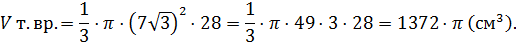
5) Площадь поверхности тела вращения равна сумме площадей боковой поверхности двух конусов:

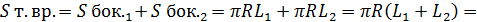
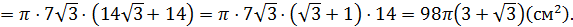
Ответ: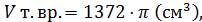

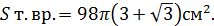
Пирамида

Определение: Пирамидой называется многогранник, в основании которого лежит произвольный многоугольник, а остальные грани являются треугольниками с общей вершиной.

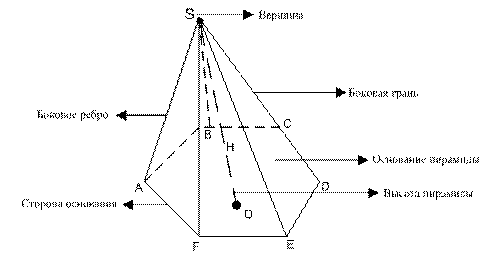
Определение: Высотой пирамиды называется отрезок перпендикуляра, опущенного из вершины пирамиды на плоскость основания пирамиды:

H = SO

Определение: Диагональная плоскость, это плоскость, проходящая через вершину пирамиды и диагональ основания.

Определение: Диагональное сечение пирамиды- это сечение, которое получается при пересечении пирамиды диагональной плоскостью. (В любой пирамиде, кроме треугольной, диагональное сечение, это треугольник).

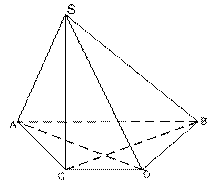
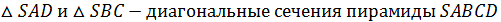
Виды пирамид:

I. Треугольная, 4-х, 5-и, 6-и угольная и так далее, в зависимости от многоугольника, лежащего в основании пирамиды.

II. Правильная и неправильная пирамида.

Определение: Пирамида называется правильной, если 1) в основании её лежит правильный многоугольник, 2) вершина пирамиды проектируется в центре основания.

Определение: Апофема- это высота боковой грани правильной пирамиды, проведённая из её вершины на сторону основания пирамиды.