К выполнению практических работ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К выполнению практических работ

по дисциплине «Математика»

для студентов первого курса специальностей

220703 Автоматизация технологических процессов и производств

(по отраслям),

230401 Информационные системы (по отраслям),

270802 Строительство и эксплуатация зданий и сооружений,

080114 Экономика и бухгалтерский учет (по отраслям)

Невинномысск 2013 г.

УДК 51 К-45

Рассмотрено на заседании ПЦК ФМД протокол №____ «___»____________2013г     Утверждено Заместитель директора по учебно-методической работе Л.В. Готра

К-45

Математика: методические указания к выполнению практических работ студентов специальностей 220703 «Автоматизация технологических процессов и производств (по отраслям)», 230401 «Информационные системы (по отраслям)», 270802 «Строительство и эксплуатация зданий и сооружений», 080114 «Экономика и бухгалтерский учет (по отраслям)»/ сост. Нелли Анатольевна Кихтенко, преподаватель высшей квалификационной категории - Невинномысск: НХК, – 2013.- 83 с.

Методические указания к выполнению практических работпредназначаются для студентов первого курса дисциплины «Математика» по специальностям 220703 «Автоматизация технологических процессов и производств (по отраслям)», 230401 «Информационные системы (по отраслям)», 270802 «Строительство и эксплуатация зданий и сооружений», 080114 «Экономика и бухгалтерский учет (по отраслям)». Пособие содержит тематический план практических работ, варианты практических заданий, указания к их выполнению, краткий теоретический материал, необходимый для выполнения практических работ, примеры типовых расчётов заданий.

Методические рекомендации составлены на основании Федерального государственного образовательного стандарта среднего профессионального образования

© Кихтенко Н.А., 2013

© ГБОУ СПО НХК, 2013

Пояснительная записка

Дисциплина «Математика» играет ведущую роль в общей и профессиональной системах образования студентов химического колледжа.

Задачи курса математики в подготовке специалистов по профессиональному обучению состоят в том, чтобы дать представление о структуре современной математики, о современных методах высшей математики, об универсальности методов и языка математики, о способах решения прикладных задач математики.

Наряду с обеспечением высокой математической подготовки обучающихся, которые в дальнейшем в своей профессиональной деятельности будут пользоваться математическими знаниями и навыками, важнейшей задачей обучения является обеспечение некоторого гарантированного уровня математической подготовки независимо от специальности.

Федеральный государственный образовательный стандарт третьего поколения среднего профессионального образования подразумевает компетентностный подход в обучении. Основной задачей преподавателя является не передача, "трансляция" знаний, а формирование у обучающихся профессиональных компетенций, методов и способов самостоятельного поиска и получения новых знаний, умения применять теоретические знания при решении практических задач. При изучении дисциплины «Математика» наибольшие трудности у студентов возникают при решении практических задач. Вместе с тем именно решение задач в значительной степени способствует развитию инженерного мышления у студентов. В связи с этим практическая работа студентов играет решающую роль при изучении курса дисциплины «Математика».

Методические указания к выполнению практических работпредназначаются для студентов первого курса дисциплины «Математика» по специальностям 220703 «Автоматизация технологических процессов и производств (по отраслям)», 230401 «Информационные системы (по отраслям)», 270802 «Строительство и эксплуатация зданий и сооружений», 080114 «Экономика и бухгалтерский учет (по отраслям)». Практические занятия обучающегося составляют 72 часа согласно учебному плану.

Целью данного пособия является помощь студенту в организации его практической работы по дисциплине. В методических указаниях перечислены темы практических работ обучающегося по всем изучаемым в курсе дисциплины «Математика» темам. Даны указания к выполнению этих практических работ.

В настоящей методической разработке дан краткий теоретический материал, необходимый для выполнения заданий, и подробно рассмотрены решения типовых заданий, а также изложены требования к выполнению и оформлению индивидуальных практических работ, предусмотренных программой курса.

В методическом пособии даны варианты индивидуальных практических заданий по каждой практической работе, приведён список рекомендуемой литературы и Интернет-ресурсов.

Методические указания к практическим работам обеспечивают формирование базовых умений для выполнения исследований в процессе научного познания и теоретического обоснования профессиональных задач.

Содержание

Пояснительная записка............................................................................................3

I. Тематический план практических работ ...........................................................6

II. Распределение практических работ по учебным темам

дисциплины " Математика "...............................................................................6

III. Методические указания к выполнению практической

работы по индивидуальным заданиям .............................................................7

IV. Список рекомендуемой литературы, Интернет-ресурсов..............................9

Приложения.............................................................................................................10

I. Тематический план практических работ

1. Действия над комплексными числами в алгебраической форме записи.

2. Решение уравнений, неравенств и систем уравнений и неравенств.

3. Вычисление пределов функции в точке и на бесконечности.

4. Решение показательных и логарифмических уравнений и неравенств.

5.Тригонометрические функции: вычисление значений тригонометрических функций, упрощение выражений, доказательство тождеств.

6. Решение тригонометрических уравнений и неравенств.

7. Векторы и координаты. Прямая и её уравнение на плоскости.

8. Прямая и плоскость в пространстве.

9. Дифференцирование функций.

10. Нахождение неопределённых и определённых интегралов.

11. Геометрические тела. Вычисление объёмов и площадей поверхности многогранников и тел вращения.

IV. Список рекомендуемой литературы, Интернет-ресурсов

Основные источники:

1. Пехлецкий И.Д. Математика: Учебник. - М.: Издательский центр "Академия", 2011. -304 с.- Серия: "Среднее профессиональное образование".

2. Дадаян А.А. Математика: Учебник.- М.: ФОРУМ-ИНФРА-М, 2005.-552 с.- Серия: "Среднее профессиональное образование".

3. Богомолов Н.В., Самойленко П.И. Математика.- М.: Дрофа, 2006.

Дополнительные источники:

1. Алгебра и начала анализа. /Под ред. Г.Н. Яковлева. Ч.1 - М.: Наука, 1987.-336 с.- Серия: учебники для средних специальных учебных заведений.

2. Алгебра и начала анализа. /Под ред. Г.Н. Яковлева. Ч.2 - М.: Наука, 1988.-360 с.- Серия: учебники для средних специальных учебных заведений.

3. Богомолов Н.В. Практические занятия по математике. - М.: Наука, 1990.

4. Геометрия. /Под ред. Г.Н. Яковлева. Ч.1 - М.: Наука, 1987. -319 с.- Серия: учебники для средних специальных учебных заведений.

5. Лисичкин В.Т., Соловейчик И.Л. Математика: Учебное пособие для техникумов. - М.: Высшая школа, 1991.- 480 с.- Серия: учебное пособие для средних специальных учебных заведений.

Интернет-ресурсы:

1. http://school-collection.edu.ru /- Единая коллекция цифровых образовательных ресурсов;

2. www.lektorium.tv- "Лекции ведущих лекторов России в свободном доступе";

3. www.youtube.com/user/msu- Лекции преподавателей МГУ им. М. Ломоносова;

4. www.youtube.com/education-объединяет учащихся и преподавателей всего мира в одной всемирной аудитории.

Приложение 1

ГБОУ СПО "НХК"

Практическая работа №1

по дисциплине «Математика» специальности

230401 Информационные системы (по отраслям)

ТЕМА: " Действия над комплексными числами в алгебраической форме "

ВАРИАНТ №

Выполнил студент группы И-11-12

Иванов Александр Сергеевич;

Проверила преподаватель

Кихтенко Нелли Анатольевна

Невинномысск

2012-2013 учебный год

Приложение 2

Практическая работа № 1

ТЕМА: " Действия над комплексными числами в алгебраической форме "

Цель работы:закрепление навыков решения уравнений, неравенств, систем уравнений и неравенств.

Умения и навыки, которые должны приобрести обучающиеся : выполнять действия с комплексными числами в алгебраической форме записи:

сложение, вычитание, умножение, деление, находить степени мнимой единицы.

Наглядные пособия, оборудование:микрокалькулятор, дидактические карточки с заданиями.

Повторение теоретических основ:

1. Комплексные числа, их геометрическое изображение.

2. Мнимая единица, степени мнимой единицы.

3. Комплексно-сопряжённые числа.

4. Алгебраическая форма записи комплексного числа.

5. Действия над комплексными числами в алгебраической форме.

6. Правило деления комплексных чисел в алгебраической форме записи.

Практика: студенты самостоятельно выполняют расчеты по выданным дидактическим карточкам – заданиям.

Приложение 3: дидактические карточки – задания (8 вариантов)

Практическая работа № 2

ТЕМА: "Решение уравнений, неравенств, систем уравнений и систем неравенств"

Цель работы: закрепление навыков решения уравнений, неравенств, систем уравнений и неравенств.

Умения и навыки, которые должны приобрести обучающиеся:решать уравнения различных видов; решать линейные неравенства и системы линейных неравенств; решать системы линейных и нелинейных уравнений; вычислять определители II и III порядка и применять теорему Крамера.

Наглядные пособия, оборудование:микрокалькулятор, дидактические карточки с заданиями.

Повторение теоретических основ:

1. Дробно-рациональное уравнение и метод его решения.

2. Биквадратные уравнения и метод их решения.

3. Иррациональные уравнения и метод их решения.

4. Линейные неравенства и системы линейных неравенств, их решение.

5. Метод интервалов при решении дробно-рациональных неравенств.

6. Решение квадратных неравенств двумя методами.

7. Определитель II порядка и правило его вычисления.

8. Определитель III порядка и правило его вычисления.

9. Решение систем линейных уравнений по формулам Крамера с помощью определителей.

10. Решение систем нелинейных уравнений:

а) методом подстановки;

б) методом введения новой переменной.

Практика: студенты самостоятельно выполняют расчеты по выданным дидактическим карточкам – заданиям.

Приложение 3: дидактические карточки – задания (8 вариантов)

Практическая работа №3

ТЕМА: " Вычисление пределов функции в точке и на бесконечности"

Цель работы: закрепить навыки вычисления пределов функции, применения теорем о пределах функции; раскрытия различных видов неопределенностей.

Умения и навыки, которые должны приобрести обучающиеся:применять теоремы о пределах функции в точке и на бесконечности, правила раскрытия неопределенностей типа 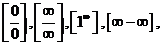применять замечательные пределы.

Наглядные пособия, оборудование: плакат с теоремами о пределах функции в точке, микрокалькулятор, дидактические карточки с заданиями.

Повторение теоретических основ:

1. Предел функции в точке (определение).

2. Бесконечно малая функция в точке (на бесконечности).

3. Бесконечно большая функция в точке (на бесконечности).

4. Теорема о связи между бесконечно малой и бесконечно большой функциями в точке.

5. Теоремы о пределах функции в точке (о сумме; произведении; частном двух функции; о постоянном множители).

6. Правило раскрытия неопределенности типа .

7. Правило раскрытия неопределенности типа .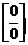

8. Замечательные пределы.

Практика: студенты самостоятельно выполняют расчеты по выданным дидактическим карточкам – заданиям.

Приложение 3:дидактические карточки с вариантами заданий(6 вариантов)

Практическая работа № 4

ТЕМА: "Решение показательных и логарифмических уравнений

и неравенств, систем уравнений"

Цель работы: закрепить навыки решения показательных и логарифмических уравнений, неравенств, систем уравнений.

Умения и навыки, которые должны приобрести обучающиеся: решать различными методами показательные и логарифмические уравнения и неравенства, решать системы уравнений, применять свойства логарифмов, свойства показательной и логарифмической функций.

Наглядные пособия, оборудование:плакаты с формулами по теме «логарифм числа», плакаты с графиками показательной и логарифмической функций; микрокалькулятор, дидактические карточки с заданиями.

Повторение теоретических основ:

1. Показательная функция, её график и свойства при 0<a<1 и при a>1.

2. Показательные уравнения и методы их решения:

а) приведение уравнения к виду ;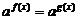

б) метод логарифмирования;

в) метод подстановки.

3. Показательные неравенства и методы их решения:

а) применение свойства показательной функции в неравенствах вида

;

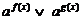б) метод подстановки.

4. Логарифмическая функция, её график и свойства при 0<a<1 и a>1.

5. Логарифмические уравнения и методы их решения:

а) приведение уравнения к виду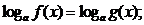

б) метод потенцирования;

в) метод подстановки.

6. Логарифмические неравенства и методы их решения:

а) применение свойств логарифмической функции в неравенствах , приведенных к виду .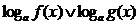

б) метод подстановки.

7. Методы решения систем логарифмических и показательных уравнений.

Практика: студенты самостоятельно выполняют расчеты по выданным дидактическим карточкам – заданиям.

Приложение 3: дидактические карточки – задания (6 вариантов).

Практическая работа №5

ТЕМА: "Тригонометрические функции: вычисление значений тригонометрических функций, упрощение выражений,

доказательство тождеств"

Цель работы: закрепление навыков применения формул по теме «Тригонометрические функции», свойств тригонометрических функций.

Умения и навыки, которые должны приобрести обучающиеся:вычислять тригонометрические выражения, доказывать тригонометрические тождества; применить правило приведения тригонометрических функций к функциям острого угла; применять свойства тригонометрических функций.

Наглядные пособия, оборудование: плакаты с формулами по теме «Тригонометрические функции»; микрокалькулятор; дидактические карточки с заданиями.

Повторение теоретических основ:

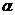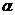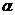1. Определение тригонометрических функций числового аргумента (sin , cos , tg , ctg ).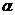

2. Знаки тригонометрических функций по четвертям.

3. Значения тригонометрических функций в некоторых углах.

4. Соотношение между тригонометрическими функциями одного аргумента (тригонометрические тождества).

5. Теоремы сложения.

6. Формулы двойного аргумента.

7. Формулы понижения степени.

8. Правило приведения тригонометрических функций к функциям острого угла.

9. Дополнительные углы и их свойства.

10. Формулы преобразования суммы или разности тригонометрических функций в произведение.

11. Четность, нечетность тригонометрических функций.

12. Периодичность тригонометрических функций.

Практика: студенты самостоятельно выполняют расчеты по выданным

дидактическим карточкам – заданиям.

Приложение 3:дидактические карточки с вариантами заданий( 8 вариантов)

Практическая работа № 6

ТЕМА: "Решение тригонометрических уравнений и неравенств"

Цель работы: закрепить навыки решения простейших тригонометрических уравнений и умение решать различные виды тригонометрических уравнений.

Умения и навыки, которые должны приобрести обучающиеся:решать простейшие тригонометрические уравнения; применять метод замены переменной; применять метод разложения левой части уравнения на множители; решать однородные тригонометрические уравнения.

Наглядные пособия, оборудование:плакаты с формулами по теме «Тригонометрические функции»; плакат с таблицей решений простейших тригонометрических уравнений; микрокалькулятор; дидактические карточки с заданиями.

Повторение теоретических основ:

1. Простейшие тригонометрические уравнения.

2. Общие формулы корней простейших тригонометрических уравнений.

3. Применение тригонометрического круга для решения уравнений вида 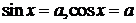при .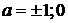

4. Метод замены переменной и приведения тригонометрического уравнения к алгебраическому уравнению.

5. Однородные тригонометрические уравнения. Метод решения однородных тригонометрических уравнений.

6. Метод решения тригонометрических уравнений разложением левой части уравнения на множители.

7. Методы разложения левой части уравнения на множители.

8. Формулы преобразования суммы или разности тригонометрических функций в произведение.

9. Решение тригонометрических уравнений вида 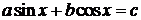. Введение вспомогательного угла.

Практика: студенты самостоятельно выполняют расчеты по выданным дидактическим карточкам – заданиям.

Приложение 3: дидактические карточки – задания (8 вариантов)

Практическая работа № 7

ТЕМА: " Векторы и координаты. Прямая и её уравнение на плоскости"

Цель работы: закрепить навыки применения различных видов уравнения прямой на плоскости при решении задач.

Умения и навыки, которые должны приобрести обучаемые на занятии:применять уравнение прямой, проходящей через две заданные точки, уравнение прямой с заданным нормальным вектором, находить середину отрезка, находить углы треугольника.

Наглядные пособия, оборудование:плакат с формулами по теме «Векторы»; плакат «Уравнение прямой на плоскости»; микрокалькулятор; дидактические карточки с заданиями.

Повторение теоретических основ:

1. Деление отрезка в данном отношении. Деление отрезка пополам.

2. Расстояние между двумя точками на плоскости. Длина вектора.

3. Скалярное произведение векторов.

4. Угол между двумя векторами. Формула .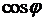

5. Уравнение прямой, проходящей через заданную точку с заданным направляющим вектором.

6. Уравнение прямой, проходящей через две заданные точки.

7. Уравнение прямой, проходящей через заданную точку с заданным нормальным вектором.

8. Условие параллельности прямых.

9. Условие перпендикулярности прямых.

10. Угол между двумя прямыми, заданными уравнениям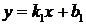и и .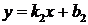

11. Общее уравнение прямой на плоскости.

Практика: студенты самостоятельно выполняют расчеты по дидактическим карточкам с заданиями.

Приложение 3: дидактические карточки с заданиями (6 вариантов)

Практическая работа № 8

ТЕМА: "Прямая и плоскость в пространстве"

Цель работы: закрепить навыки применения полученных теоретических знаний по теме «Прямые и плоскости в пространстве» при решении задач.

Умение и навыки, которые должны приобрести обучающиеся:находить расстояние от точки до плоскости и до прямой; находить угол между прямой и плоскостью; применять теорему о трех перпендикулярах; находить длину наклонной и её проекции на плоскость.

Наглядные пособия, оборудование: геометрические модели к задачам, микрокалькулятор, дидактические карточки с заданиями.

Повторение теоретических основ:

1. Определение параллельности прямой и плоскости.

2. Теорема о признаке параллельности прямой и плоскости.

3. Теорема о трех перпендикулярах.

4. Наклонная и перпендикуляр к плоскости.

5. Угол между наклонной и плоскостью.

6. Расстояние от точки до плоскости.

7. Расстояние от точки до прямой.

8. Определение параллельных прямых.

9. Определение параллельных плоскостей.

10. Теорема о признаке параллельности двух плоскостей.

11. Теорема о транзитивности параллельности прямых и плоскостей.

Практика: студенты самостоятельно выполняют задания по дидактическим карточкам.

Приложение 3: дидактические карточки с заданиями

Практическая работа № 9

ТЕМА: "Дифференцирование функций"

Цель работы: закрепить навыки нахождения производной функции, умение дифференцировать сложную функцию.

Умения и навыки, которые должны приобрести обучающиеся:дифференцировать различные функции, применять правила и формулы дифференцирования, дифференцировать сложную функцию.

Наглядные пособия, оборудования: таблицы с формулами дифференцирования, микрокалькулятор, дидактические карточки с заданиями.

Повторение теоретических основ:

1. Производная функции (определение).

2. Механический смысл производной.

3. Общее правило нахождения производной.

4. Правила дифференцирования суммы, произведения, частного двух функций: ; ; ; .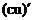

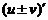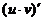5. Таблица производных основных элементарных функций.

6. Сложная функция (определение).

7. Правило дифференцирования сложной функции.

8. Примечания к правилу дифференцирования функций.

Практика: студенты самостоятельно выполняют расчеты по выданным дидактическим карточкам – заданиям.

Приложение 3: дидактические карточки с вариантами заданий (8 вариантов)

Практическая работа №10

Тема: "Неопределенный и определенный интегралы"

Цель работы: закрепить навыки непосредственного интегрирования, применения метода подстановки при нахождении неопределенного интеграла, вычисления определенного интеграла.

Умения и навыки, которые должны приобрести обучающиеся:находить неопределенный интеграл различными методами, применять формулу Ньютона-Лейбница при вычислении определенного интеграла; находить путь, пройденный телом при неравномерном движении с помощью определенного интеграла.

Наглядные пособия, оборудование: плакат с формулами интегрирования; микрокалькулятор; дидактические карточки с заданиями.

Повторение теоретических основ:

1. Неопределенный интеграл (определение).

2. Свойства неопределенного интеграла.

3. Приёмы непосредственного интегрирования.

4. Метод подстановки при вычислении неопределенного интеграла.

5. Определенный интеграл (определение).

6. Свойства определенного интеграла.

7. Формула Ньютона-Лейбница.

8. Правило вычисления определенного интеграла.

9. Вычисление пути, пройденного телом при неравномерном движении с помощью определенного интеграла.

Практика: студенты самостоятельно выполняют расчеты по выданным дидактическим карточкам – заданиям.

Приложение 3: дидактические карточки – задания (8 вариантов)

Практическая работа № 11

ТЕМА: "Геометрические тела. Вычисление объёмов и площадей поверхности многогранников и тел вращения"

Цель работы: закрепление навыков вычисления объемов и площадей поверхности различных геометрических тел.

Умения и навыки, которые должны приобрести обучающиеся:находить объем и площадь поверхности призмы, параллелепипеда, пирамиды, конуса, цилиндра, шара.

Наглядные пособия, оборудование: модели геометрических тел; плакаты с изображениями фигур; микрокалькулятор; дидактические карточки с заданиями.

Повторение теоретических основ:

1. Призма; правильная призма.
2. Теорема о площади боковой поверхности призмы.
3. Площадь полной поверхности призмы:

a) правильной треугольной;

б) правильной четырехугольной.

1. Объем призмы. Объем прямой призмы.
2. Параллелепипед. Виды параллелепипедов:

а) прямой параллелепипед;

б) прямоугольный параллелепипед;

в) куб.

1. Объем и площадь поверхности прямоугольного параллелепипеда.
2. Объем куба. Площадь полной поверхности куба.

8. Диагональное сечение призмы, параллелепипеда, прямоугольного

параллелепипеда, куба.

1. Пирамида. Виды пирамид.
2. Правильная пирамида. Апофема.
3. Теорема о площади боковой поверхности правильной пирамиды.
4. Правильная треугольная пирамида:

а) площадь основания;

б) площадь полной поверхности.

1. Правильная четырехугольная пирамида:

а) площадь основания;

б) площадь полной поверхности.

13. Объем пирамиды.

1. Конус; элементы конуса (образующая, высота, радиус основания).
2. Площадь основания конуса; площадь боковой поверхности конуса;

площадь полной поверхности конуса.

1. Объем конуса.
2. Цилиндр; элементы цилиндра.
3. Площадь боковой поверхности цилиндра; площадь основания

цилиндра; площадь полной поверхности цилиндра.

1. Объем цилиндра.
2. Шар; осевое сечение шара. Площадь осевого сечения шара.
3. Площадь поверхности шара.
4. Площадь сечения шара плоскостью, проведенной на расстоянии d от центра шара радиуса R.
5. Объем шара.

Практика: студенты самостоятельно выполняют расчеты по выданным дидакти-ческим карточкам – заданиям.

Приложение 3: дидактические карточки – задания (6 вариантов)

Приложение 4

Методические указания и примеры типового расчёта

Теория

Теоремы о пределах функции в точке и на бесконечности:

1) О пределе суммы функций:
;

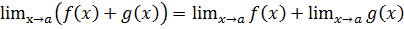2) О пределе разности функций:

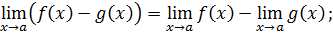
3) О пределе произведения функции:
;

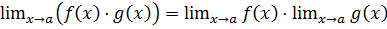4) О пределе деления частного двух функций:
;

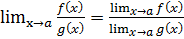5) Постоянный множитель можно вынести за знак предела:
.

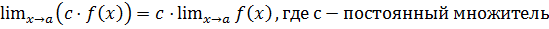Правило №1.Чтобы раскрыть понятие неопределённости вида 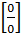, нужно и числитель и знаменатель разложить на простейшие множители и сократить дробь, тогда неопределённость исчезнет и можно применять теоремы о пределах.

Правило №2.Чтобы избавиться от неопределённости вида 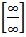, нужно одновременно и числитель и знаменатель дроби разделить на 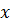в наивысшей степени, тогда неопределённость исчезнет и можно применять теоремы о пределах.

Пример 1.Вычислить предел функции:

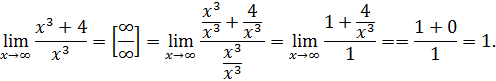
Методические указания и примеры типового расчёта

Теория

Основные соотношения между функциями одного и того же угла:

; ;

; ; ; ; .

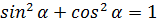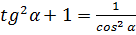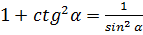
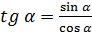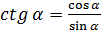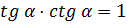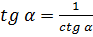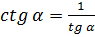Формулы двойного угла: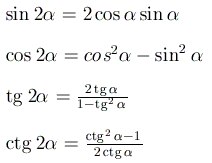

Знаки тригонометрических функций по четвертям:

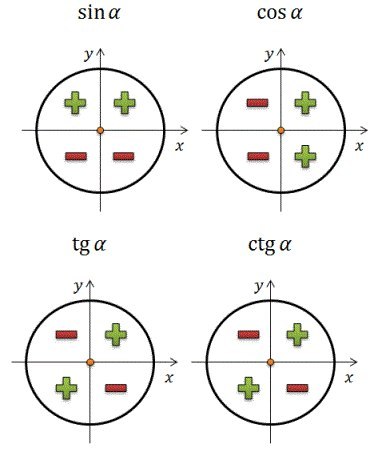
Задание 1

Дано: .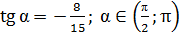

Найти: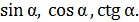

Решение:

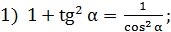тогда 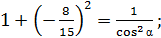отсюда находим

;
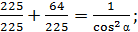
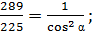
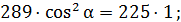
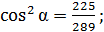
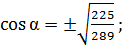
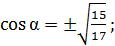
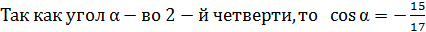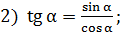тогда

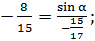
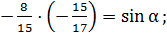
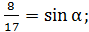
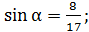
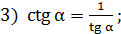тогда

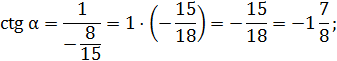
Ответ: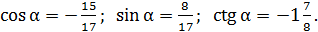

Задание 2

Дано: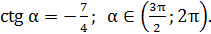

Найти: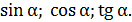

Решение:

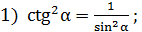тогда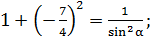

.

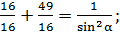
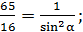
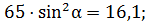
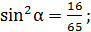
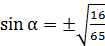Так как, α- угол 4-й четверти, то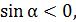

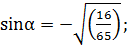или 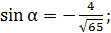вычисляем с точностью до сотых

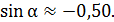
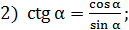тогда 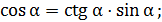подставляем числовые значения

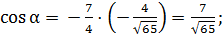вычисляем с точностью до сотых

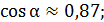
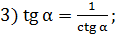вычисляем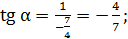

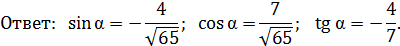
Задание 3

I. Привести угол к табличному и вычислить значения тригонометрической функции:

1)

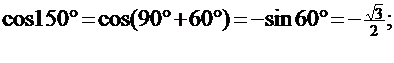
2)

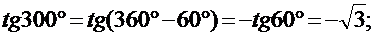
3)

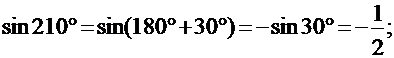
4)

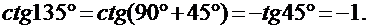
II. Не изменяя название тригонометрической функции привести к острому углу:

1)

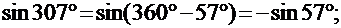
2)

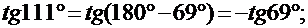
3)

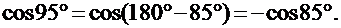
III. Используя свойства нечетности, четности, периодичности тригонометрических функций вычислить:

1) Вычислить: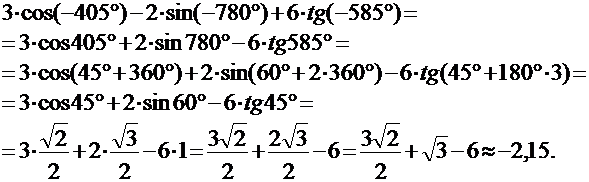

2)

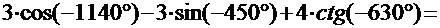
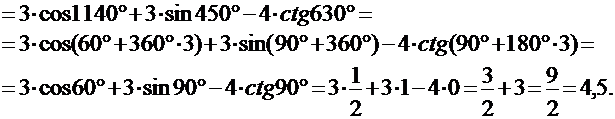
3) Вычислить значение тригонометрического выражения: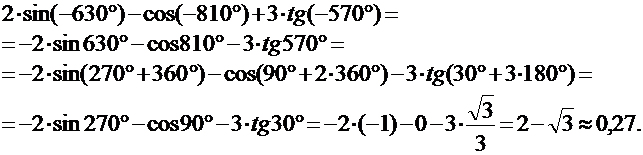

4) Вычислить:

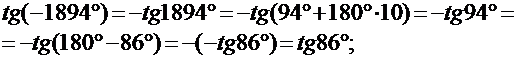
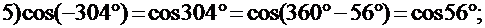
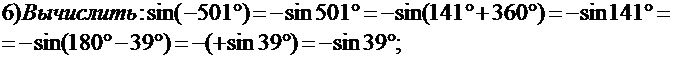
7) Вычислить: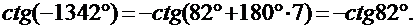

Методические указания и примеры типового расчёта

Теория

Простейшими тригонометрическими уравнениями называются уравнения вида

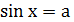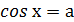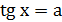, , или .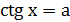

При 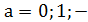1 для решения уравнений удобно пользоваться тригонометрическим кругом.

В остальных случаях будем применять общую формулу корней тригонометрического уравнения, которая приведена в таблице решений простейших тригонометрических уравнений.

Таблица решений простейших тригонометрических уравнений

Уравнение вида	Общая формула корней уравнения	Промежуток главного угла
	,

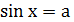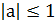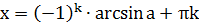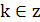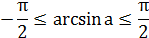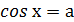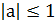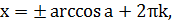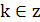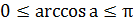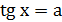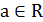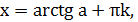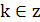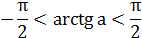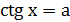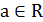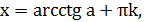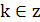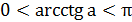Примеры типовых расчётов

1) Решить уравнение: .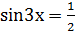

Решение:

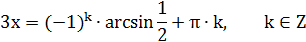
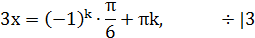
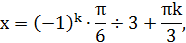
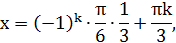
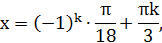
Ответ: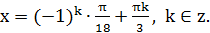

Найти 3 корня этого уравнения:

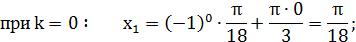
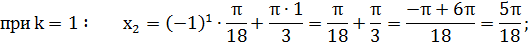
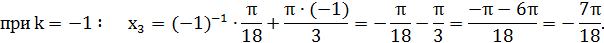
Ответ: .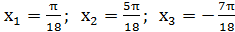

Вывод: убедились, что в общей формуле корней тригонометрического уравнения содержится бесчисленное множество решений.

2) Решит уравнение: