Генеральной совокупности. Критерий согласия Пирсона
В предыдущих параграфах закон распределения генеральной совокупности предполагался известным.
Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А.
Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины — критерия согласия.
Определение 1. Критерием согласияназывают критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Имеется несколько критериев согласия: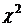 
, Пирсона, Колмогорова, Смирнова и др.
Ограничимся описанием применения критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.
Обычно эмпирические и теоретические частоты различаются (см. пример 3.1, начало).
Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности.
Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает, на принятом уровне значимости, ее согласие или несогласие с данными наблюдений.
Пусть по выборке объема п получено эмпирическое распределение:
 |  |  | … |  |
 |  |  | … |  |
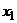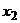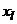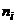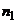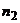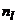Допустим, что в предположении нормального распределения генеральной совокупности, вычислены теоретические частоты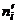 
. При уровне значимости 
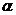требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.
В качестве критерия проверки нулевой гипотезы примем случайную величину
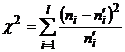. (4.1)
Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (4.1). Следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.
Замечание. Возведение в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей. Делением на 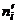достигают уменьшения каждого из слагаемых; в противном случае сумма была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива. Разумеется, приведенные соображения не являются обоснованием выбранного критерия, а лишь пояснением.
Доказано, что при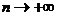 
закон распределения случайной величины (4.1), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения 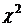с k степенями свободы. Поэтому случайная величина (4.1) обозначена через 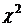, а сам критерий называют критерием согласия «хи квадрат».
Число степеней свободы находят по равенству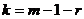 
, где 
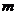— число групп (частичных интервалов) выборки; 
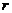— число параметров предполагаемого распределения, которые оценены по данным выборки.
Замечание.В частности, если предполагаемое распределение — нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение) поэтому 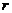=2 и число степеней свободы 
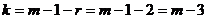. Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр 
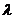, поэтому 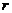=1 и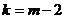 
.
Поскольку односторонний критерий более «жестко» отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости :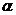 
.
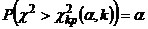Таким образом, правосторонняя критическая область определяется неравенством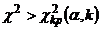 
, а область принятия нулевой гипотезы – неравенством 
.
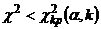Обозначим значение критерия, вычисленное по данным наблюдений, через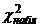 
и сформулируем правило проверки нулевой гипотезы.
Правило.Для того чтобы, при заданном уровне значимости, проверить нулевую гипотезу Н0: генеральная совокупность распределена нормально, надо:
1)вычислить теоретические частоты ,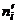
2)наблюдаемое значение критерия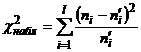 
,
3)по таблице критических точек распределения 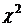по заданному уровню значимости 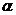, и числу степеней свободы 
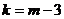, найти критическую точку 
.
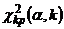4)Если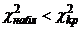 
— нет оснований отвергнуть нулевую гипотезу.
Если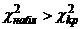 
— нулевую гипотезу отвергают.
Замечание 1. Объем выборки должен быть достаточно велик, во всяком случае не менее 50. Каждая группа должна содержать не менее 5—8 вариант; малочисленные группы следует объединять в одну, суммируя частоты.
Замечание 2. Поскольку возможны ошибки первого и второго рода, в особенности, если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями, построить график распределения, вычислить асимметрию и эксцесс.
Замечание 3. В целях контроля вычислений, формулу 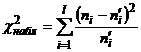преобразуют к виду 
.
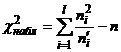Пример 3.1 (продолжение). При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности.
Решение. Составим расчётную таблицу.
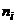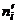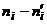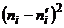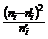| № | | | |  |  |  | Контрольные вычисления | |
 |  | |||||||
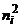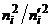| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | ||||||||
| 6. | ||||||||
| 7. | ||||||||
| 8. | ||||||||
| 9. | ||||||||
Число степеней свободы:
Критическая точка:
Вывод:
§ 4. Проверка гипотезы о значимости
выборочного коэффициента корреляции
Пусть двумерная генеральная совокупность (X, У) распределена нормально. Из этой совокупности извлечена выборка объема п и по ней найден выборочный коэффициент корреляции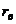 
который оказался отличным от нуля. Так как выборка отобрана случайно, то еще нельзя заключить, что коэффициент корреляции генеральной совокупности 
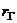также отличен от нуля. В конечном счете, нас интересует именно этот коэффициент, поэтому возникает необходимость, при заданном уровне значимости 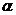, проверить нулевую гипотезу Н0: 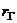=0 о равенстве нулю генерального коэффициента корреляции, при конкурирующей гипотезе 
.
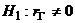Если нулевая гипотеза будет отвергнута, то это означает, что выборочный коэффициент корреляции значимо отличается от нуля (коротко: значим), а X и У коррелированы, т. е. связаны линейной зависимостью.
Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции незначим, а X и У некоррелированы, т. е. не связаны линейной зависимостью.
В качестве критерия проверки нулевой гипотезы примем случайную величину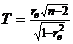 
. Величина Т, при справедливости нулевой гипотезы, имеет распределение Стьюдента с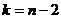 
Поскольку конкурирующая гипотеза имеет вид 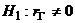, критическая область — двусторонняя; она строится, исходя из требования, чтобы вероятность попадания критерия Т в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости 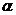. При этом наибольшая мощность критерия достигается пр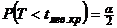и 
и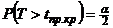 
. Так как распределение Стьюдента симметрично относительно нуля, то и критические точки симметричны относительно нуля. Обозначим 
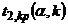– правую границу двусторонней критической области. Тогда левая граница примет вид: 
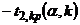, двусторонняя критическая область: 
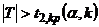, область принятия нулевой гипотезы 
.
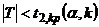Обозначим значение критерия, вычисленное по данным наблюдений, через Тнабл и сформулируем правило проверки нулевой гипотезы.
Правило. Для того чтобы при заданном уровне значимости 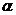, проверить нулевую гипотезу Н0: 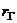=0 о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины, при конкурирующей гипотезе 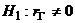, надо:
1)вычислить наблюдаемое значение критерия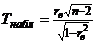 
2) по таблице критических точек распределения Стьюдента по заданному уровню значимости и числу степеней свободы 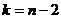, найти критическую точку 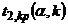для двусторонней критической области.
Если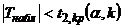 
— нет оснований отвергнуть нулевую гипотезу.
Если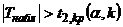 
— нулевую гипотезу отвергают.
ПРИЛОЖЕНИЕ 1
Таблица значений функции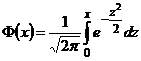 
.
 |  | | | | | | |
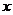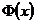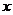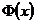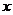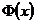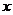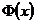| 0,00 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0,99 | 0,3389 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,00 | 0,3413 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1,09 | 0,3621 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1,10 | 0,3643 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 1,11 | 0,3665 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 1,12 | 0,3686 |
| 0,17 | 0,0675 | 0,49 | 0,1879 | 0,81 | 0,2910 | 1,13 | 0,3708 |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1,21 | 0,3869 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0,3883 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1,24 | 0,3925 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | ||
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 |
Продолжение приложения 1
| | | | | | | | |
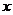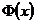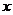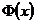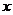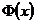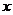| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0,4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0,4484 | 1,96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0,4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0,4099 | 1,67 | 0,4525 | 2,00 | 0,4772 | 2,66 | 0,4961 |
| 1,35 | 0,4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0,4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0,4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0,4162 | 1,71 | 0,4564 | 2,08 | 0,4812 | 2,74 | 0,4969 |
| 1,39 | 0,4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1,40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1,41 | 0,4207 | 1,74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1,42 | 0,4222 | 1,75 | 0,4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1,43 | 0,4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1,44 | 0,4251 | 1,77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0,4265 | 1,78 | 0,4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1,46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1,47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1,81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0,4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1,50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2,98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1,52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1,53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3,40 | 0,49966 |
| 1,54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,499841 |
| 1,55 | 0,4394 | 1,88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,499928 |
| 1,56 | 0,4406 | 1,89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,499968 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,499997 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,499997 |
ПРИЛОЖЕНИЕ 2
Таблица значений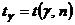 
.
| g n | 0,95 | 0,99 | 0,999 | g n | 0,95 | 0,99 | 0,999 |
| 2,78 | 4,60 | 8,61 | 2,093 | 2,861 | 3,883 | ||
| 2,57 | 4,03 | 6,86 | 2,064 | 2,797 | 3,745 | ||
| 2,45 | 3,71 | 5,96 | 2,045 | 2,756 | 3,659 | ||
| 2,37 | 3,50 | 5,41 | 2,032 | 2,720 | 3,600 | ||
| 2,31 | 3,36 | 5,04 | 2,023 | 2,708 | 3,558 | ||
| 2,26 | 3,25 | 4,78 | 2,016 | 2,692 | 3,527 | ||
| 2,23 | 3,17 | 4,59 | 2,009 | 2,679 | 3,502 | ||
| 2,20 | 3,11 | 4,44 | 2,001 | 2,662 | 3,464 | ||
| 2,18 | 3,06 | 4,32 | 1,996 | 2,649 | 3,439 | ||
| 2,16 | 3,01 | 4,22 | 1,991 | 2,640 | 3,418 | ||
| 2,15 | 2,98 | 4,14 | 1,987 | 2,633 | 3,403 | ||
| 2,13 | 2,95 | 4,07 | 1,984 | 2,627 | 3,392 | ||
| 2,12 | 2,92 | 4,02 | 1,980 | 2,617 | 3,374 | ||
| 2,11 | 2,90 | 3,97 | ¥ | 1,960 | 2,576 | 3,291 | |
| 2,10 | 2,88 | 3,92 |
ПРИЛОЖЕНИЕ 3
Таблица значений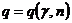 
.
| g n | 0,95 | 0,99 | 0,999 | g n | 0,95 | 0,99 | 0,999 |
| 1,37 | 2,67 | 5,64 | 0,37 | 0,58 | 0,88 | ||
| 1,09 | 2,01 | 3,88 | 0,32 | 0,49 | 0,73 | ||
| 0,92 | 1,62 | 2,98 | 0,28 | 0,43 | 0,63 | ||
| 0,80 | 1,38 | 2,42 | 0,26 | 0,38 | 0,56 | ||
| 0,71 | 1,20 | 2,06 | 0,24 | 0,35 | 0,50 | ||
| 0,65 | 1,08 | 1,80 | 0,22 | 0,32 | 0,46 | ||
| 0,59 | 0,98 | 1,60 | 0,21 | 0,30 | 0,43 | ||
| 0,55 | 0,90 | 1,45 | 0,188 | 0,269 | 0,38 | ||
| 0,52 | 0,83 | 1,33 | 0,174 | 0,245 | 0,34 | ||
| 0,48 | 0,78 | 1,23 | 0,161 | 0,226 | 0,31 | ||
| 0,46 | 0,73 | 1,15 | 0,151 | 0,211 | 0,29 | ||
| 0,44 | 0,70 | 1,07 | 0,143 | 0,198 | 0,27 | ||
| 0,42 | 0,66 | 1,01 | 0,115 | 0,160 | 0,211 | ||
| 0,40 | 0,63 | 0,96 | 0,099 | 0,136 | 0,185 | ||
| 0,39 | 0,60 | 0,92 | 0,089 | 0,120 | 0,162 |
ПРИЛОЖЕНИЕ 4
Таблица значений функции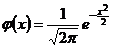 
| 7 | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 |
Продолжение прилож. 4
| á | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,0044 | |||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 |
ПРИЛОЖЕНИЕ 5
Критические точки распределения c2
| Число степеней | Уровень значимости a | |||||
| свободы k | 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 |
| 6,6 | 5,0 | 3,8 | 0,0039 | 0,00098 | 0,00016 | |
| 9,2 | 7,4 | 6,0 | 0,103 | 0,051 | 0,020 | |
| 11,3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 | |
| 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 | |
| 15,1 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 | |
| 16,8 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 | |
| 18,5 | 16,0 | 14,1 | 2,17 | 1,69 | 1,24 | |
| 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 | |
| 21,7 | 19,0 | 16,9 | 3,33 | 2,70 | 2,09 | |
| 23,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 | |
| 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 | |
| 26,2 | 23,3 | 21,0 | 5,23 | 4,40 | 3,57 | |
| 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 | |
| 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 | |
| 30,6 | 27,5 | 25,0 | 7,26 | 6,26 | 5,23 | |
| 32,0 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 | |
| 33,4 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 | |
| 34,8 | 31,5 | 28,9 | 9,39 | 8,23 | 7,01 | |
| 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 | |
| 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 | |
| 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,90 | |
| 40,3 | 36,8 | 33,9 | 12,3 | 11,0 | 9,54 | |
| 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | 10,2 | |
| 43,0 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 | |
| 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 | |
| 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 | |
| 47,0 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 | |
| 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 | |
| 49,6 | 45,7 | 42,6 | 17,7 | 16,0 | 14,3 | |
| 50,9 | 47,0 | 43,8 | 18,5 | 16,8 | 15,0 |
ПРИЛОЖЕНИЕ 6