Отыскание критических областей
Обоснование задачи поиска критической области требует привлечения достаточно сложной теории. Практические методы отыскания критической области позволяют решать эту задачу по определённым алгоритмам. Из определения критических областей следует, что для отыскания правосторонней или левосторонней критических областей достаточно найти 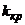 . Для этого:
. Для этого:
1) Задают достаточно малую вероятность – уровень значимости 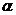 .
.
2)С помощью специальных таблиц (см. Приложения) ищут критическую точку 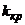 , исходя из требования, чтобы, при условии справедливости нулевой гипотезы, в зависимости от вида области выполнялось одно из условий:
, исходя из требования, чтобы, при условии справедливости нулевой гипотезы, в зависимости от вида области выполнялось одно из условий:
| Для правосторонней критической области | Вероятность того, что критерий К примет значение, большее 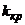 , была равна принятому уровню значимости , была равна принятому уровню значимости | 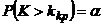 |
| Для левосторонней критической области | Вероятность того, что критерий К примет значение, меньшее 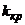 , была равна принятому уровню значимости , была равна принятому уровню значимости | 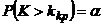 |
| Для двусторонней критической области | Сумма вероятностей того, что критерий примет значение меньшее 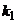 или большее или большее 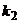 была равна принятому уровню значимости была равна принятому уровню значимости | 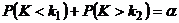 или или 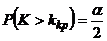 |
Замечание 1.Критические точки двусторонней критической области могут быть выбраны бесчисленным множеством способов. Если же распределение критерия симметрично относительно нуля и имеются основания (например, для увеличения мощности критерия (см. следующий пункт)) выбрать симметричные относительно нуля точки 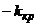 и
и 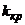 (
( 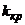 >0), то
>0), то 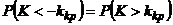 . Учитывая равенство
. Учитывая равенство 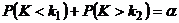 , получим
, получим 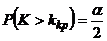 . Это соотношение и служит для отыскания точек двусторонней критической области.
. Это соотношение и служит для отыскания точек двусторонней критической области.
Замечание 2. Когда критическая точка уже найдена, вычисляют по данным выборок наблюдаемое значение критерия, а затем делают вывод о принятии или непринятии нулевой гипотезы:
| Для правосторонней критической области | 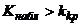 | Нулевую гипотезу отвергают |
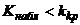 | Нулевую гипотезу принимают | |
| Для левосторонней критической области | 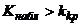 | Нулевую гипотезу принимают |
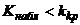 | Нулевую гипотезу отвергают |
Пояснение.Почему правосторонняя критическая область была определена, исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение 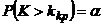 ?
?
Поскольку вероятность события 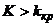 мала (
мала ( 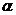 – малая вероятность), такое событие, при справедливости нулевой гипотезы, в силу принципа практической невозможности маловероятных событий, в единичном испытании не должно наступить. Если все же оно произошло, т. е. наблюдаемое значение критерия оказалось больше
– малая вероятность), такое событие, при справедливости нулевой гипотезы, в силу принципа практической невозможности маловероятных событий, в единичном испытании не должно наступить. Если все же оно произошло, т. е. наблюдаемое значение критерия оказалось больше 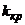 , то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование
, то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование 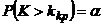 определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они и составляют правостороннюю критическую область.
определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они и составляют правостороннюю критическую область.
Замечание 3. Наблюдаемое значение критерия может оказаться большим 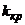 не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости
не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости 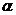 . Итак, пользуясь требованием
. Итак, пользуясь требованием 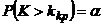 , мы с вероятностью
, мы с вероятностью 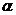 рискуем совершить ошибку первого рода.
рискуем совершить ошибку первого рода.
В книгах по контролю качества продукции, вероятность признать негодной партию годных изделий называют «риском производителя», а вероятность принять негодную партию – «риском потребителя».
Замечание 4. Пусть нулевая гипотеза принята. Ошибочно думать, что тем самым она доказана. Действительно, известно, что один пример, подтверждающий справедливость некоторого общего утверждения еще не доказывает его. Поэтому более правильно говорить «данные наблюдений согласуются с нулевой гипотезой и, следовательно, не дают оснований ее отвергнуть».
На практике, для большей уверенности принятия гипотезы, ее проверяют другими способами, или повторяют эксперимент, увеличив объем выборки.
Отвергают гипотезу более категорично, чем принимают. Действительно, известно, что достаточно привести один пример, противоречащий некоторому общему утверждению, чтобы это утверждение отвергнуть. Если оказалось, что наблюдаемое значение критерия принадлежит критической области, то этот факт и служит примером, противоречащим нулевой гипотезе, что позволяет ее отклонить.
