Более сложные случаи корреляции

Если график линии регрессии или представляет собой кривую линию, то корреляция называется криволинейной. Встречаются квадратичная, кубическая, показательная и т. д. корреляции. Соответственно их линии регрессии описываются квадратичной, кубической, показательной и т. д. функциями. Функция регрессии имеет большое значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной.

Несмотря на важность понятия функции регрессии, возможности ее практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид распределения двумерной случайной величины . Только зная вид этого распределения, можно точно определить вид функции регрессии, а затем оценить его параметры. Однако, для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения , а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек на плоскости можно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены.

Если исследуется связь между несколькими признаками, то корреляция называется множественной. Метод, позволяющей по выборке, которая содержит отдельные наблюдавшиеся значения переменных , , 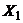, 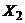…, 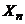оценить параметры зависимости, называется множественной регрессией. Коэффициенты уравнения множественной регрессии также определяются по методу наименьших квадратов.

Если признаки не поддаются количественной оценке, то используется ранговая корреляция.

Ранговая корреляция

B некоторых случаях приходится иметь дело с признаками, не поддающимися количественной оценке. Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле, что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако, этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.

Пусть п индивидуумов имеют по качеству А следующие ранги: Х₁, Х₂, ..., Х_п, а по качеству В — ранги Y₁, Y₂, ..., Y_п, где все X и Y являются перестановками п первых чисел натурального ряда. Обозначим разность X_k—Y_k = d_k. Значения σ_k образуют меру тесноты соответствия между A и В. Если все σ_k равны нулю, то соответствие полное.

Наиболее удобный коэффициент измерения тесноты связи можно получить следующим образом. Поскольку значения рангов X расположены от 1 до п, их сумма, как сумма чисел натурального ряда, равна , аих средняя равна . Таково же среднее значение рангов Y. Обозначим через x_k отклонение X_k от средней, т. е. . Аналогично, . Найдем коэффициент корреляции по формуле (3.1)*:

. (4.1)

Этот коэффициент называется коэффициентом корреляции рангов Спирмена. Его можно выразить через п и σ_k, Действительно,

.

Далее имеем , откуда . После подстановки выражений для , и в формулу (4.1) получаем .

Коэффициент корреляции рангов изменяется от +1 до —1. Если все значения σ_k равны нулю, то . Если ранги таковы, что 1-й, 2-й, ..., n-й по одному признаку соответствуют п, (п—1), ..., 1 по другому признаку, то .

Если нельзя установить ранговое различие нескольких сложных индивидуумов, то берут средний ранг. В этом случае коэффициент корреляции рангов Спирмена вычисляется по формуле

,

где , — число объединенных рангов.

Существуют и другие показатели тесноты связи между рангами. Это, например, коэффициент корреляции рангов Кенделла. Предложенный им коэффициент более труден для вычислений, однако, им удобно пользоваться при углубленных исследованиях.

Пусть п индивидуумов имеют по качеству А следующие ранги: Х₁, Х₂, ..., Х_п, а по качеству В — ранги Y₁, Y₂, ..., Y_п, где все X и Y являются перестановками п первых чисел натурального ряда. Допустим, что правее Y₁ имеется R₁ рангов, больших Y₁; правее Y₂ имеется R₂ рангов, больших Y₂; …; правее имеется рангов, больших . Выборочный коэффициент ранговой корреляции Кенделла вычисляется по формуле:

.

Коэффициент корреляции рангов может быть применен для быстрого оценивания отношения между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены по тем или иным причинам.