Для чего нужен гармонический анализ? Основные расчетные формулы. Интерпретация полученных результатов. Как при помощи гармонического анализа можно выполнить фильтрацию временного ряда

Многие природные процессы являются периодическими, т.е. воспроизводятся в прежнем виде через определенный промежуток времени Т (смена времен года, смена дня и ночи, продолжительность светового дня и т.д.). С точки зрения математики, различные величины, связанные с рассматриваемыми периодическими процессами, по истечение периода Т возвращаются к своим прежним значениям и являются периодическими функциями от времени t: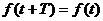

Гармонический анализ – это процесс разложения периодической функции в ряд Фурье (на гармоники). Гармоника (гармонические составляющие функции f(t)) – отдельные синусоидальные величины, входящие в состав тригонометрического ряда. Ибо периодическая функция f(t) периода Т (при этом составляющие синусоидальные величины разных частот) может быть представлена в виде суммы конечного или бесконечного множества синусоид. Интерпретация полученных результатов: с помощью гармонического анализа можно выделить низко-, средне- и высокочастотные колебания, а также оценить вклад отдельных гармоник в исследуемый процесс.

Задача гармонического анализа заключается в построении практически удобных методов для приближенного определения коэффициентов ряда Фурье или для непосредственного вычерчивания гармоник различных порядков для функции, заданной таблично. По этим коэффициентам можно судить о вкладе отдельных гармоник: если k≈0, то вклад гармоник минимальный, а если k≈1, то это основные гармоники. По ним можно составлять гипотезы и процессооформирующих явлениях.

Пусть ф-ия f(x) – периодическая с периодом 2π: f(x+2π)=f(x). Основная задача гармонического анализа – представить ф-цию f(x) в виде ряда: 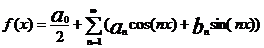, где коэф. ряда определяется по формулам Эйлера-Фурье: ; ;

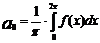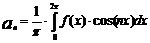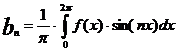
Полагая что 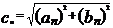, , 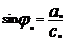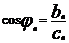ряд можно представить в ви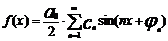де: , где 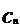- амплитуда гармоники, 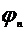- фаза

Ряд Фурье и гармонический анализ позволяют выполнить фильтрацию временного ряда. Напр.:

*Если обнулить n-компонент (с низкими частотами), то это высокочастотная фильтрация;

*Если удалить все компоненты с какой-то высокой частотой, то это будет низкочастотная фильтрация;

*Обнулив компонент со значениями частот «от и до» - полосовая фильтрация.

Иногда фильтрация с пропусканием высоких частот производится путем вычитания сглаженных величин из данного ряда, в рез-те в ряду остаются только высокие частоты.

1)Фильтрация низких и высоких частот, в рез-те чего в ряду остаются средние частоты. Иногда эти частоты получаются путем дополнительного сглаживания ряда данных, полученных путем вычитания первоначального сглаживания величин из экспериментального ряда.

2)Существуют фильтры позволяющие усилить высокие частоты. Этим достигается ликвидация эффекта предыдущего сглаживания (процесс «обратного сглаживания»).

Простейшими фильтрами являются скользящая средняя и взвешенная скользящая средняя.

Для чего необходимо осреднение? Основные расчетные формулы метода скользящего среднего и экспоненциального сглаживания. Интерпретация полученных результатов. Достоинства и недостатки данных двух методов

Осреднение необходимо для исключения влияния на анализ флуктуаций – короткопериодические колебания, медленные постепенные изменения случайной переменной в течение всего анализируемого периода и колебания, хар-ся промежуточным временным масштабом.

Метод скользящей средней заключается в том, что для каждого аргумента берется средняя арифметическая на несколько соседних значениях функции.

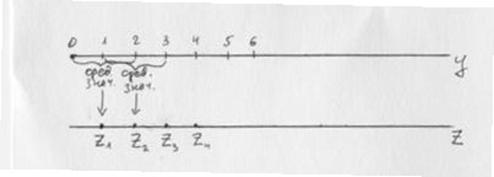
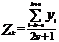, т.е. ;

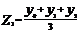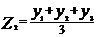
Пропадут первые v-точки и последние v-точки: 2v-точки.

Применяют для длинных рядов, где пропажа двух крайних 2v-точек ничего не решает. Характерно для физ.-географов и не характерно для эконом.географов, которые работают с небольшими рядами. Многоцелевой, легко программируемый метод, однако велика вероятность неточности.

Метод взвешенной скользящей средней является более точным, т.к. не связан с потерей крайних значений. Для этих целей добавляют с обеих концов ряда по два члена, расчет производится по формуле: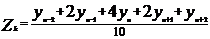

Метод экспоненциального сглаживания. Пусть есть некоторый ряд 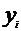, где i=1,2,..n. Тогда расчетные формулы имеют вид:

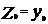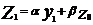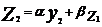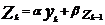; …	α и β > 0 α+β=1 α ~ 0,1-0,3 (т.е. берут значение в этом пределе) Чем меньше α, тем больше степень осреднения

Его преимущества заключаются в простоте вычислений, гибкости описаний динамик процессов. Метод экспоненциального сглаживания дает возможность получить оценку параметров тренда, хар-щих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения. Наибольшее применение метод нашел для коротких рядов в геоэкологии и эконом.географии. Для метода экспоненциального сглаживания основным и наиболее трудным моментом является выбор параметра сглаживания α и начальных условий.

Интерпретация полученных результатов: воспользовавшись рассмотренными методами, мы сократили, сжали набор полученных результатов и осреднили их, что избавило нас от ряда процессов обработки не столь важных результатов. (например, для оценки численности населения не так важно знать его каждодневное количество)