Геометрический смысл производной.

Теорема 1:

График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке.

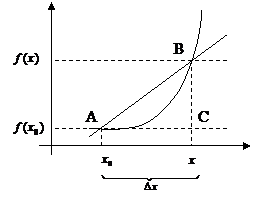
Доказательство:

Пусть существует значение f’( )-конечное, тогда

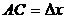
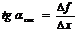
при

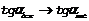
Секущая стремится к касательной.

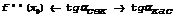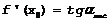=> ч.т.д.

Пусть существует невертикальная касательная => существует 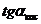- конечный.

Секущая стремится к касательной.

=>

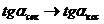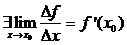
Теорема доказана.

Билет 3

Арифметические свойства производной.

Пусть f = f(x) и g = g(x) – функции, имеющие конечные производные в точке x₀, тогда справедливы равенства:

1.

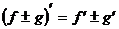
2.

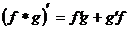
2.1. 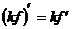где k – константа

3.

-----------------------------------------------------------------------------------------------------------------------------

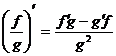
1.

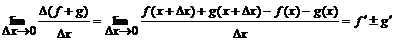
2.

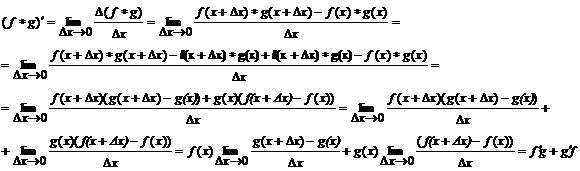
Заметим, что функция f , как имеющая производную, непрерывна, и потому при

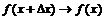
3.

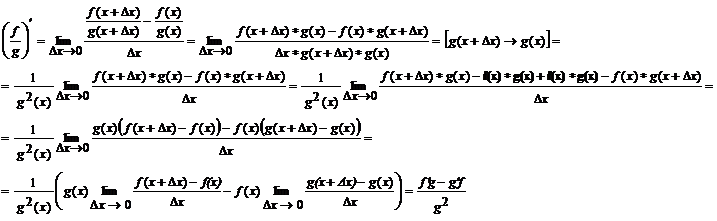
Билет 4

Производная обратной функции.

Определение: Пусть на интервале (a,b) задана непрерывная строго монотонная, т.е. строго возрастающая или строго убывающая, функция 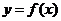. Пусть образ (a,b) есть интервал (A,B). тогда обратная к функция 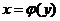есть однозначная непрерывная и строго монотонная на (A,B) функция.

Зафиксируем 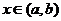и дадим ему приращение 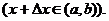Тогда 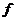получит соответствующее приращение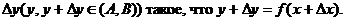

Наоборот,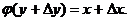

Вследствие непрерывности прямой и обратной функций для указанных 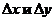имеет место утверждение: из 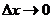следует 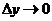, и обратно.

Пусть теперь функция 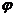в точке у имеет неравную нулю производную 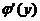. Покажем, что в таком случае функция 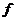также имеет в соответствующей точке х производную. В самом деле,

Так как из того, что 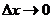следует, ч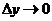то , то

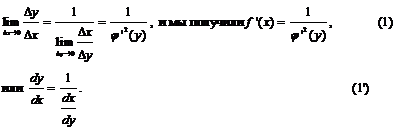
Этим доказано, что если 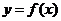есть строго монотонная непрерывная функция и 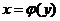обратная к ней функция, имеющая в точке у производную 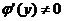, то функция 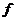имеет в соответствующей точке х производную, определяемую формулой (1).

Может случится, что в точке 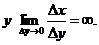В этом случае, очевидно, функция 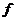имеет в соответствующей точке х производную .

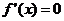Если же 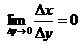, то для строго возрастающей функции при этом 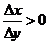, а для строго убывающей 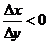. В первом случае 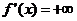, а во втором .

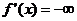Пример 1.

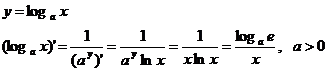
Если логарифм натуральный, то

.

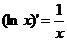Функция ln x как действительная функция определена только для положительных значений х.

Пример 2.

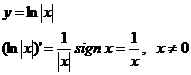
где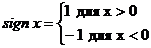

Пример 3.

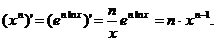
Пример 4.

Функция 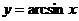строго возрастает на отрезке [-1,1] и отображает этот отрезок на 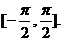Обратная к ней функция 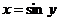имеет производную 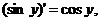положительную на интервале 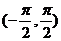. Поэтому

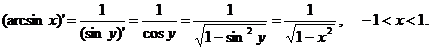
Пример 5.

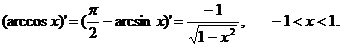
Пример 6.

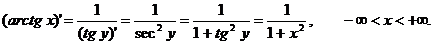
Билет 5

Производная сложной функции.

Теорема:

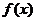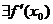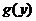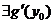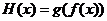Пусть функция такая, что , и функция такая, что , . Тогда функция и .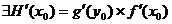

Доказательство:

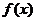дифференцируема в точке 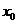, тогда:

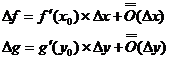
Рассмотрим ∆H:

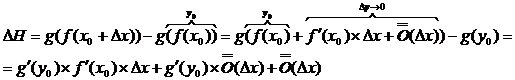
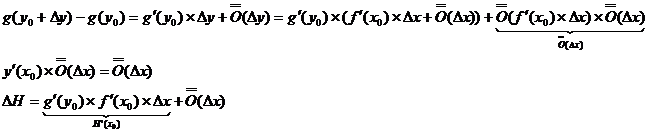
Билет 6

Производные элементарных функций.

1. ;

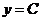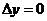
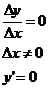
2.

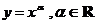
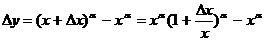
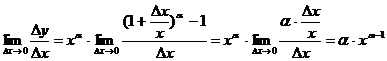
3.

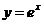
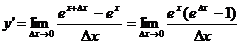
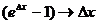
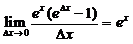
4.

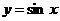
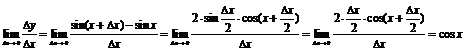(т.к. функция непрерывна)

Замечание: если функция имеет конечную производную в точке, то она непрерывна в этой точке (было доказано в Билете 1), но она может быть разрывной в любой другой точке, кроме этой.

Пример:

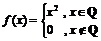
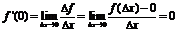, т.к.

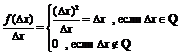
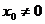
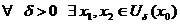
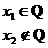
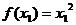
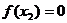
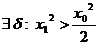
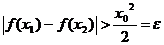
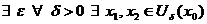
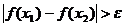- не выполняется критерий Коши и в каждой точке 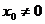функция разрывна.

Билет 7