Интегрирование выражений, содержащих квадратный трехчлен.
Оглавление
Введение 4
1 Производная функции 5
1.1 Вопросы для самопроверки 7
2 Приложение производной к исследованию функции
и построению ее графика 8
2.1 Вопросы для самопроверки 10
3 Неопределенный интеграл 10
3.1 Метод замены переменного 11
3.2 Интегрирование по частям 12
3.3 Интегрирование выражений, содержащих
квадратный трехчлен 14
3.4 Интегрирование рациональных дробей 17
3.5 Вопросы для самопроверки 22
4 Определенный интеграл 22
4.1 Основные свойства определенного интеграла 23
4.2 Правила вычисления определенного интеграла 23
4.3 Приложения определенного интеграла 25
4.3.1 Вычисление площадей плоских фигур 25
4.3.2 Вычисление объемов тел вращения 26
4.3.3 Вычисление длины дуги кривой 26
4.4 Вопросы для самопроверки 27
5 Индивидуальные задания для контрольной работы №2 27
Библиографический список 36
Введение
Целью настоящих методических указаний является помощь студентам – заочникам в выполнении контрольной работы №2.
Работа содержит 9 заданий по различным разделам дифференциального и интегрального исчислений.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы [1] – [3] и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях. Большое количество образцов решенных задач дано в руководстве к решению задач [5]. Задачи для самостоятельного решения имеются как в представленных методических указаниях, так и в сборниках задач [4], [6].
Номер варианта по каждому заданию студент выбирает по формуле 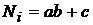 ,
,
где 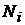 - номер варианта
- номер варианта
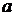 -номер задания,
-номер задания,
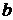 -предпоследняя цифра шифра студента,
-предпоследняя цифра шифра студента,
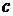 -последняя цифра шифра.
-последняя цифра шифра.
Пример.
Пусть шифр студента 1235, тогда:
номер варианта первого задания: 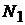 =
= 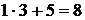 ;
;
номер варианта второго задания: 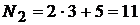 ;
;
номер варианта третьего задания: 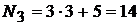 ;
;
номер варианта четвертого задания: 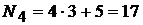 ;
;
номер варианта пятого задания: 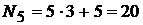 ;
;
номер варианта шестого задания: 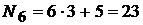 …
…
Если получается число больше 20, то для определения варианта берут их разность. В нашем случае это будет 23-20=3. Следовательно, студент, имеющий шифр 1235, должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом, №20 – в пятом, №3 – в шестом и т.д.
1 Производная функции
Понятие производной функции является одним из основных в математике и широко применяется в различных областях науки и техники.
Производной функции y=f(x) в точке х 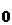 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю произвольным образом.
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю произвольным образом.
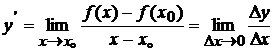 .
.
Процедура отыскания производной называется дифференцированием функции.
Справедливы следующие правила дифференцирования:
1. (с)  =0 2. (u+v)
=0 2. (u+v)  =u
=u  +v
+v  3. (uv)
3. (uv)  =u
=u  v+uv
v+uv 
4. (сu)  = сu
= сu  5.
5. 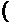
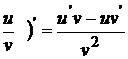 .
.
На основе этого определения могут быть выведены формулы для производных основных элементарных функций:
1. 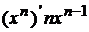 , в частности:
, в частности: 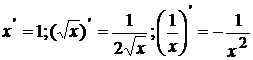 ;
;
2. 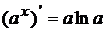 , в частности:
, в частности: 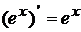 ;
;
3. 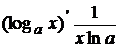 , в частности:
, в частности: 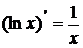 ;
;
4. 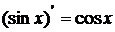 ; 5.
; 5. 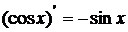 ;
;
6. 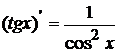 ; 7.
; 7. 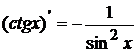 ;
;
8. 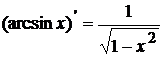 ; 9.
; 9. 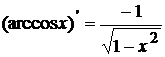 ;
;
10. 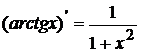 ; 11.
; 11. 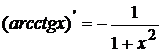 .
.
Особый интерес представляет производная сложной функции.
Если у=f(u), где u= 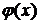 , тогда у
, тогда у 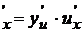 .
.
Пример 1 Найти производную функции: 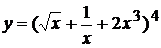 .
.
Решение.
Используя правило дифференцирования сложной функции, а также формулу нахождения производной степенной функции, получим:
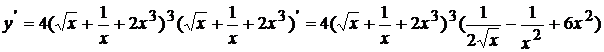 .
.
Пример 2 Найти производную функции 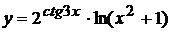 .
.
Решение.
Воспользуемся правилом дифференцирования произведения двух функций и формулами нахождения производной от показательной и логарифмической функции.
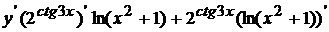 = =
= = 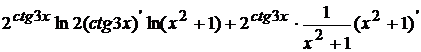 = =
= = 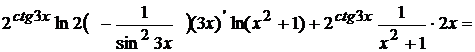
= 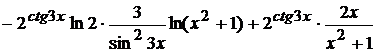 .
.
Пример 3 Найти производную функции: 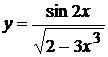 .
.
Используем правило дифференцирования дроби и формулы нахождения производной от 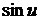 и степенной функции.
и степенной функции.
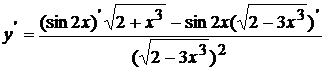 =
=
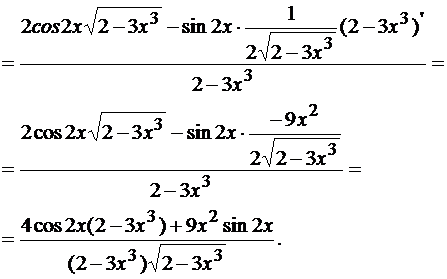
Пример 4 Найти производную функции: 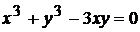 .
.
Решение.
При нахождении производной неявно заданной функции продифференцируем обе части уравнения по переменной 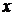 , имея в виду, что
, имея в виду, что 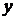 есть функция от
есть функция от 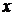 и выразим
и выразим 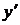 из полученного линейного относительно
из полученного линейного относительно 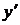 уравнения.
уравнения.
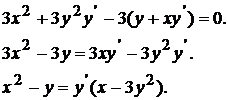
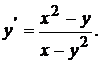
Если функция задана параметрическими уравнениями, то ее производная по переменной 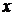 находится по формуле
находится по формуле 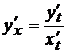 .
.
Пример 5 Найти производную функции: 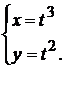
Решение.
Поскольку 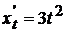 ,
, 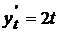 , то
, то
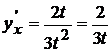 .
.
Пример 6 Найти производную функции: 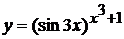 .
.
Решение.
Применим метод логарифмического дифференцирования, для чего логарифмируем заданное выражение по основанию « 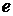 », потом дифференцируем и находим у
», потом дифференцируем и находим у  .
.
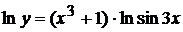 .
.
Дифференцируем:
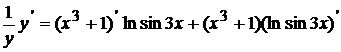 =
=
= 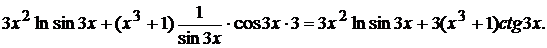
Находим из полученного уравнения у  :
:
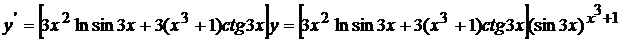 .
.
Вопросы для самопроверки
1. Что называется производной функции?
2. Каковы правила нахождения производных от суммы, произведения, дроби, от постоянной величины?
3. Как найти производную сложной функции?
4. Правило дифференцирования функции, заданной неявно.
5. В чем заключается метод логарифмического дифференцирования?
Приложение производной к исследованию функции
И построению ее графика
Методы дифференциального исчисления позволяют исследовать функции и строить их графики. Так, по знаку первой производной в интервале можно определить возрастание (убывание) функции, делать выводы о наличии или отсутствии экстремума функции. По знаку второй производной выделяем интервалы выпуклости (вогнутости) графика функции и точки перегиба ее графика.
Справедливы следующие теоремы:
1. Если функция 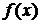 дифференцируема на интервале
дифференцируема на интервале 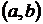 и
и 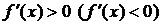 для
для 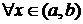 , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале 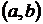 .
.
2. Если дифференцируемая функция 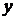 =
= 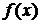 имеет экстремум в точке х
имеет экстремум в точке х 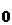 , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю: 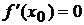 .
.
3. Если непрерывная функция 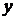 =
= 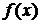 дифференцируема в некоторой
дифференцируема в некоторой 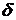 -окрестности критической точки х
-окрестности критической точки х 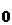 и при переходе через нее (слева направо) производная
и при переходе через нее (слева направо) производная 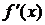 меняет знак с плюса на минус, то х
меняет знак с плюса на минус, то х 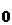 - точка максимума; с минуса на плюс, то х
- точка максимума; с минуса на плюс, то х 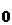 - точка минимума.
- точка минимума.
4. Если функция 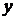 =
= 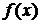 во всех точках интервала
во всех точках интервала 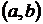 имеет отрицательную вторую производную, то график функции в этом интервале выпуклый верх; если
имеет отрицательную вторую производную, то график функции в этом интервале выпуклый верх; если 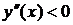 , то график выпуклый вниз.
, то график выпуклый вниз.
5. Если вторая производная 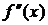 при переходе через точку х
при переходе через точку х 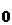 , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х
, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х 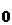 - точка перегиба.
- точка перегиба.
Построение графика функции значительно облегчается, если известны его асимптоты.
Различают 2 вида асимптот:
а) Вертикальные, существующие в точках разрыва второго рода. Их уравнения имеют вид 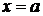 .
.
б) Наклонные: 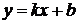 , где
, где
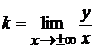 ,
, 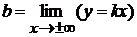 .
.
В частности, при 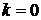 наклонная асимптота становится горизонтальной и имеет уравнение
наклонная асимптота становится горизонтальной и имеет уравнение 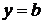 .
.
При исследовании функции и построении ее графика полезно воспользоваться следующей схемой:
1. Найти область определения функции.
2. Найти точки пересечения графика с осями координат, если это возможно.
3. Найти асимптоты графика функции.
4. Найти интервалы монотонности и точки экстремума функции.
5. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
На основании полученного исследования построить график.
Пример 7 Исследовать функцию и построить ее график:
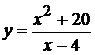 .
.
Решение.
1. Область определения.
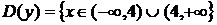 .
.
2. Асимптоты графика:
а) вертикальная 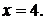
б) наклонная 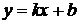 , где
, где
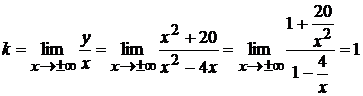 .
.
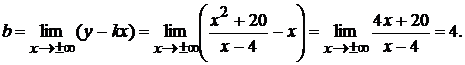
3. Найдем производную функции.
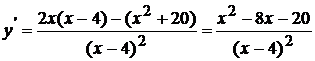 ;
; 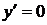 ;
; 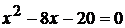 .
.
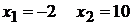 .
.
Определим знак производной в промежутках:
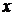 | ( 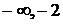 ) ) | -2 | -2, 4 | (4, 10) | (10, + 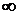 ) ) | ||
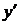 | + | - | не сущ. | 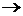 | + | ||
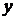 |  | max |  |  | min |  |
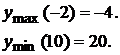
4. Найдем вторую производную функции.
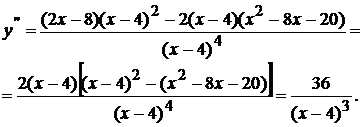
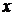 | ( 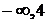 ) ) | (4, + 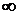 ) ) | |
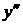 | - | не сущ. | + |
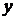 | 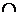 | 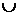 |
Точек перегиба графика функции нет.
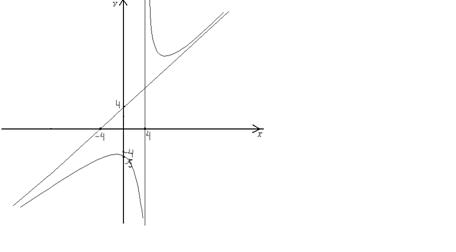 По результатам исследования построим график функции.
По результатам исследования построим график функции.
Вопросы для самопроверки
1. Каковы признаки возрастания и убывания функции?
2. Что называется экстремумом функции?
3. Сформулируйте необходимые и достаточные признаки существования экстремума функции.
4. Как найти интервалы выпуклости и вогнутости кривой и точки перегиба графика функции?
5. Что называется асимптотой кривой?
6. Каких видов бывают асимптоты графика функции и как их найти?
Неопределенный интеграл
Функция 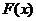 называется первообразной функции
называется первообразной функции 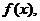 если
если 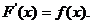 Множество первообразных функции
Множество первообразных функции 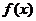 называется неопределенным интегралом и обозначается
называется неопределенным интегралом и обозначается 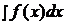 .
.
Операции дифференцирования и интегрирования взаимнообратны:
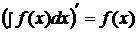 ,
,
поэтому нетрудно получить следующую таблицу интегралов:
1) 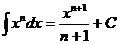 (
( 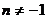 ), 7)
), 7) 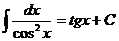 ,
,
2) 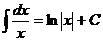 , 8)
, 8) 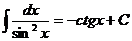 ,
,
3) 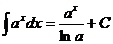 , 9)
, 9) 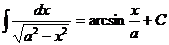 ,
,
4) 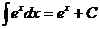 , 10)
, 10) 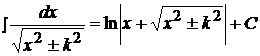 ,
,
5) 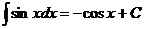 , 11)
, 11) 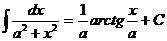 ,
,
6) 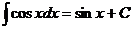 , 12)
, 12) 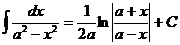 .
.
Не останавливаясь на непосредственном интегрировании по формулам, как на простейшем способе решения примеров, перейдём сразу к более сложным методам.
Метод замены переменного
Пусть требуется найти неопределенный интеграл от непрерывной функции 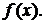
Рассмотрим некоторую функцию 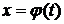 , которая имеет непрерывную производную
, которая имеет непрерывную производную 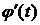 и обратную функцию
и обратную функцию 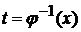 . (Например:
. (Например: 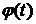 монотонна). Тогда справедлива формула:
монотонна). Тогда справедлива формула:
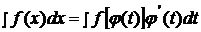 . (3.1.1)
. (3.1.1)
В некоторых ситуациях удается подобрать функцию 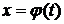 так, что интеграл в правой части (3.1.1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:
так, что интеграл в правой части (3.1.1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:
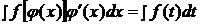 . (3.1.2)
. (3.1.2)
Другими словами, если подынтегральное выражение может быть записано в форме левой части (3.1.2), то с помощью подстановки 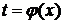 получаем более простой интеграл (3.1.1).
получаем более простой интеграл (3.1.1).
Пример 8 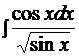 .
.
Решение.
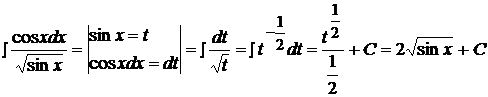 .
.
Пример 9 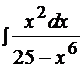 .
.
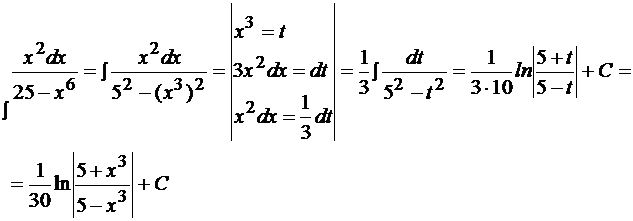
На практике часто используется следующая простая формула:
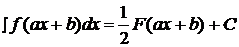 ,
,
где 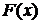 - первообразная функции
- первообразная функции 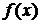 .
.
Пример 10. 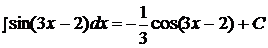 .
.
Пример 11. 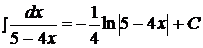 .
.
Пример 12. 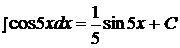 .
.
Интегрирование по частям
Формула интегрирования получается почленным интегрированием формулы производной произведения.
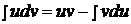 .
.
Смысл формулы заключается в том, что производная перебрасывается с одного множителя не другой и интеграл при этом может оказаться проще, чем исходный.
Можно выделить по крайней мере два класса интегралов, для которых применима формула интегрирования по частям.
I. 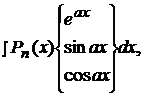
где 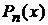 - многочлен степени
- многочлен степени 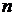 . В качестве
. В качестве 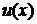 нужно взять
нужно взять 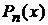 , а
, а 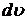 =
= 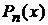 - другой сомножитель.
- другой сомножитель.
При этом формулу приходится применить столько раз, какова степень многочлена.
II. 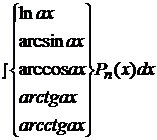 .
.
В этом случае, наоборот, следует положить 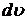 =
= 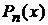 .
.
Рассмотрим применение указанной схемы.
Пример 13.
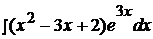 .
.
Это интеграл первого типа, поэтому:
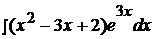 =
= 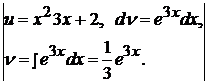 =
=
= 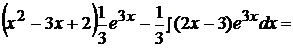
 =
=
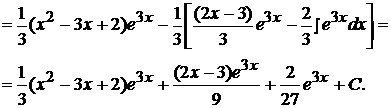
Пример 14. 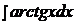 .
.
Решение.
Это интеграл второго типа, поэтому имеем:
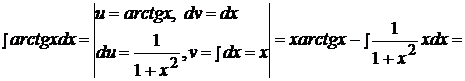
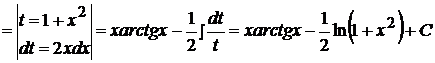 .
.
Заметим, что при использовании формулы интегрирования по частям приходится восстанавливать функцию 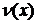 по ее дифференциалу
по ее дифференциалу 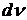 . Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.
. Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.
Формула интегрирования по частям может хорошо сработать и в других случаях.
Пример 15 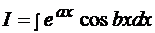 .
.
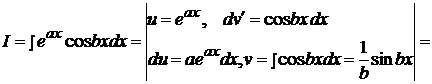
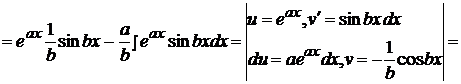
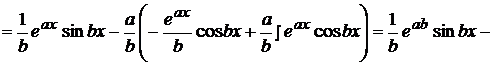
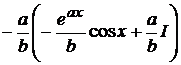 .
.
Получили уравнение относительного исходного интеграла I. Вынося I за скобку, получим
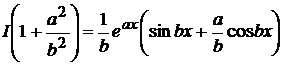 ,
,
откуда
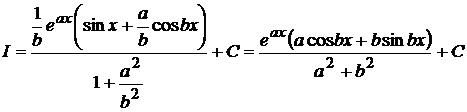 .
.
Вопросы для самопроверки
1. Что называется первообразной?
2. Сформулируйте основные свойства неопределенного интеграла.
3. В чем заключается метод замены переменной?
4. Какие функции целесообразно интегрировать по частям? Почему?
5. Как разложить рациональную дробь на простейшие?
Определенный интеграл
Пусть функция 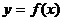 определена на отрезке
определена на отрезке 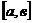 . Разобьём этот отрезок на части точками
. Разобьём этот отрезок на части точками 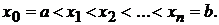 Получим
Получим 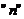 частичных отрезков длиной
частичных отрезков длиной 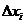 =
= 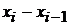 каждый.
каждый.
В каждом частичном отрезке выберем произвольную точку 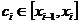 и вычислим в ней значение функции
и вычислим в ней значение функции 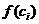 .
.
Составим сумму произведений:
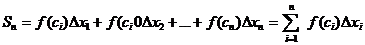 .
.
Эта сумма называется интегральной суммой функции 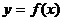 на отрезке
на отрезке 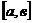 . Перейдем к пределу в последнем выражении, когда максимальный из отрезков
. Перейдем к пределу в последнем выражении, когда максимальный из отрезков 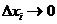 .
.
Если при этом сумма 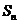 имеет предел
имеет предел 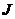 , не зависящей от способа разбиения отрезка
, не зависящей от способа разбиения отрезка 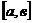 на части и от выбора точек
на части и от выбора точек 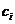 в них, то число
в них, то число 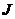 называют определенным интегралом от функции
называют определенным интегралом от функции 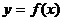 на отрезке
на отрезке 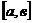 :
:
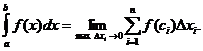
В таких случаях функцию 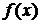 называют интегрируемой на отрезке
называют интегрируемой на отрезке 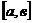 и для нее справедлива теорема, утверждающая, что любая непрерывная на отрезке
и для нее справедлива теорема, утверждающая, что любая непрерывная на отрезке 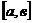 функция, является интегрируемой.
функция, является интегрируемой.
Вопросы для самопроверки
1. Что называется интегральной суммой для функции 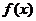 на отрезке
на отрезке 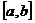 ?
?
2. Что называется определенным интегралом?
3. Каковы геометрический и физический смыслы определенного интеграла?
4. Назовите основные свойства определенного интеграла.
5. Назовите основные методы (правила) вычисления определенного интеграла.
6. Перечислите основные приложения определенного интеграла.
5 Индивидуальные задания для контрольной работы №2
Задача №1
Найти производные функций
1. а) 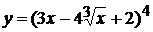 , б)
, б) 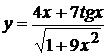 ,
,
в) 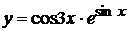 , г)
, г) 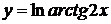 ,
,
д) 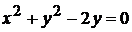 .
.
2. а) 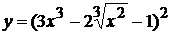 , б)
, б) 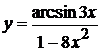 ,
,
в) 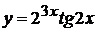 , г)
, г) 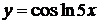 ,
,
д) 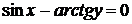 .
.
3. а) 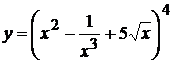 , б)
, б) 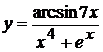 ,
,
в) 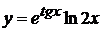 , г)
, г) 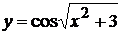 .
.
д) 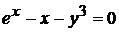 .
.
4. а) 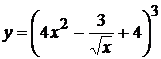 , б)
, б) 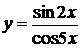 ,
,
в) 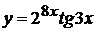 , г)
, г) 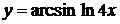 ,
,
д) 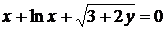 .
.
5. а) 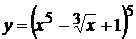 , б)
, б) 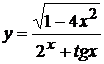 ,
,
в) 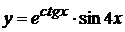 , г)
, г) 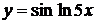 ,
,
д) 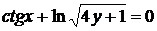 .
.
6. а) 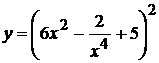 , б)
, б) 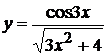 ,
,
в) 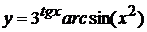 , г)
, г) 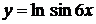 ,
,
д) 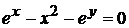 .
.
7. а) 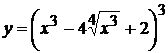 , б)
, б) 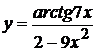 ,
,
в) 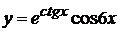 , г)
, г) 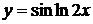 ,
,
д) 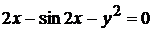 .
.
8. а) 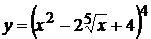 , б)
, б) 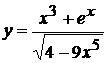 ,
,
в) 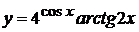 , г)
, г) 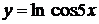 ,
,
д) 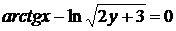 .
.
9. а) 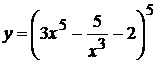 , б)
, б) 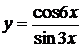 ,
,
в) 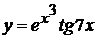 , г)
, г) 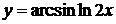 ,
,
д) 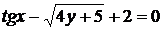 .
.
10. а) 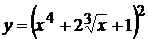 , б)
, б) 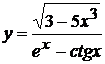 ,
,
в) 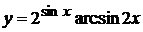 , г)
, г) 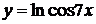 ,
,
д) 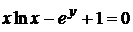 .
.
11. а) 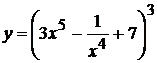 , б)
, б) 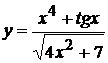 ,
,
в) 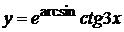 , г)
, г) 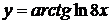 ,
,
д) 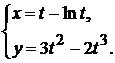
12. а) 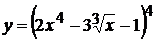 , б)
, б) 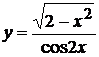 ,
,
в) 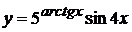 , г)
, г)  ,
,
д) 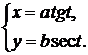
13. а) 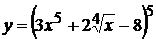 , б)
, б) 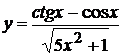 ,
,
в) 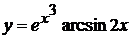 , г)
, г) 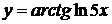 ,
,
д) 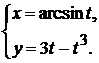
14. а) 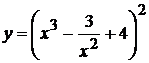 , б)
, б) 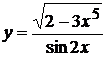 ,
,
в) 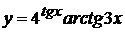 , г)
, г) 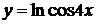 ,
,
д) 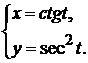
15. а) 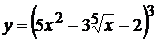 , б)
, б) 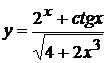 ,
,
в) 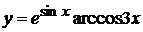 , г)
, г) 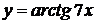 ,
,
д) 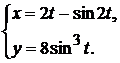
16. а) 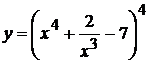 , б)
, б) 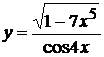 ,
,
в) 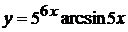 , г)
, г) 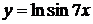 ,
,
д) 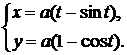
17. а) 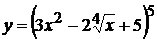 , б)
, б) 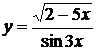 ,
,
в) 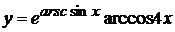 , г)
, г) 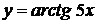 ,
,
д) 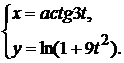
18. а) 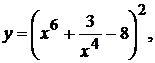 б)
б) 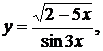
в) 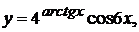 г)
г) 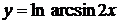 ,
,
д) 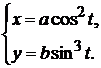
19. а) 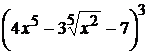 , б)
, б) 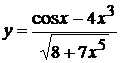 ,
,
в) 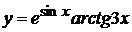 , г)
, г) 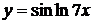 ,
,
д) 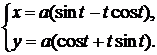
20. а) 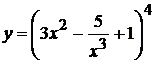 , б)
, б) 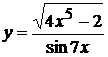 ,
,
в) 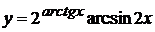 , г)
, г) 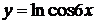 ,
,
д) 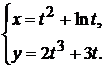
Задача №2
Исследовать функцию методами дифференциального исчисления и построить ее графики:
1. 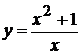 . 7.
. 7. 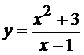 . 14.
. 14. 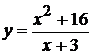 .
.
2. 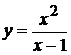 . 8.
. 8. 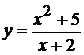 . 15.
. 15. 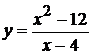 .
.
3. 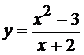 . 9.
. 9. 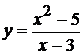 . 16.
. 16. 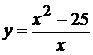 .
.
4. 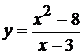 . 10.
. 10. 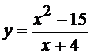 . 17.
. 17. 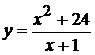 .
.
5. 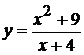 . 11.
. 11. 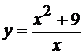 . 18.
. 18. 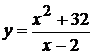 .
.
6. 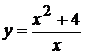 . 12.
. 12. 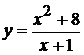 . 19.
. 19. 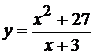 .
.
13. 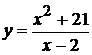 . 20.
. 20. 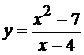 .
.
Задача №3
Найти неопределенные интегралы способом подстановки (методом замены переменного).
1. 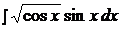 7.
7. 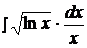 14.
14. 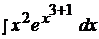
2. 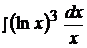 8.
8. 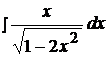 15.
15. 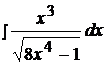
3. 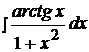 9.
9. 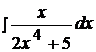 16.
16. 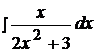
4. 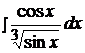 10.
10. 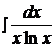 17.
17. 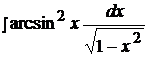
5. 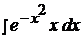 11.
11. 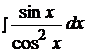 18.
18. 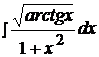
6. 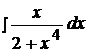 12.
12. 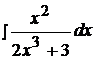 19.
19. 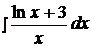
13. 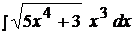 20.
20. 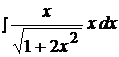
Задача №4
Найти неопределенные интегралы, используя выделение полного квадрата.
1. 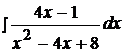
 11.
11. 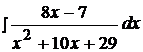
2. 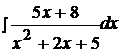 12.
12. 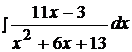
3. 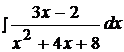 13.
13. 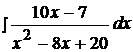
4. 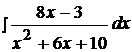 14.
14. 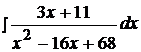
5. 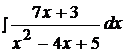 15.
15. 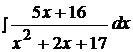
6. 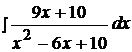 16.
16. 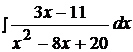
7. 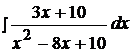 17.
17. 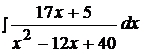
8. 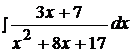 18.
18. 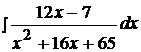
9. 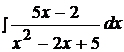 19.
19. 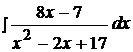
10. 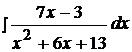 20.
20. 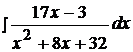
Задача №5
Найти неопределенные интегралы, применяя метод интегрирования по частям.
1. 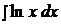
 11.
11. 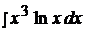
2. 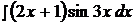 12.
12. 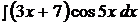
3. 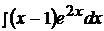 13.
13. 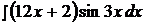
4. 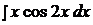 14.
14. 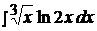
5. 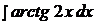 15.
15. 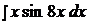
6. 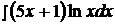 16.
16. 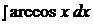
7. 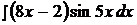 17.
17. 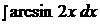
8. 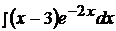 18.
18. 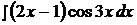
9. 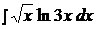 19.
19. 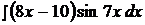
10. 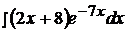 20.
20. 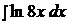
Задача №6
Найти неопределенные интегралы, пользуясь разложением рациональных дробей на простейшие.
1. 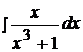
 11.
11. 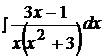
2. 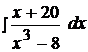 12.
12. 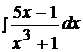
3. 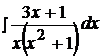 13.
13. 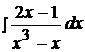
4. 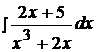 14.
14. 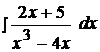
5. 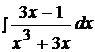 15.
15. 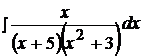
6. 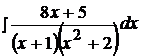 16.
16. 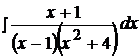
7. 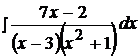 17.
17. 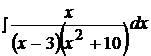
8. 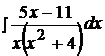 18.
18. 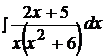
9. 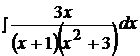 19.
19. 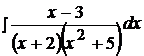
10. 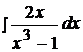 20.
20. 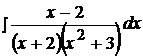
Задача №7
Вычислить площадь, ограниченную заданными параболами.
1. y= 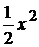 -x+1; 7. у=2
-x+1; 7. у=2 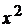 -6х+1;
-6х+1;
у= - 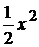 +3x+6. у= -
+3x+6. у= - 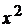 +х-1.
+х-1.
2. y= 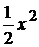 +x+2; 8. у=
+x+2; 8. у= 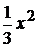 -2х+4;
-2х+4;
y= - 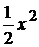 -5x+7. у= -
-5x+7. у= - 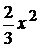 -х+2.
-х+2.
3. y= 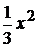 -3x+2; 9. у=
-3x+2; 9. у= 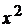 -5х-3;
-5х-3;
y= - 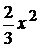 -2x+4. у= - 3
-2x+4. у= - 3 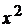 +2х-1.
+2х-1.
4. y=2 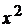 +6х-3; 10. у=
+6х-3; 10. у= 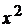 -2х-5;
-2х-5;
y= - 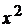 +х+5. у= -
+х+5. у= - 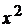 -х+1.
-х+1.
5
