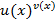Понятие производной функции, ее геометрический смысл.
Производной функции y’(x), f’(x) называетсяпредельное значение приращения функции к приращению аргумента 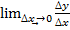
Геометрический смысл-tg угла наклона касательной к графику функции.
Правая и левая производные.
Правой(левой) производной функции y=f(x) называется правое(левое) предельное значение отношения приращения функции 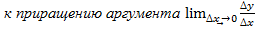
F’(x+0) правая производная, F’(x-0) левая производная.
Дифференцируемость функции(определение. Теорема26).
Функция называется дифференцируемой в т. X, если ее приращение Δy ( в этой точке), соответствующее приращению аргумента Δx, равно Δy=A* Δx+o(Δx) не зависит от Δx.
Для того, чтобы функция была дифференцируемой в точке x0 необходимо и достаточно, чтобы она имела этой точке конечную производную.
Необходимость-считается, что функция дифференцируема в точке x0. Надо доказать, что она имеет в этой точке производную. По определению дифференциала функции Δy= 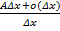 =>
=> 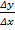 =A+
=A+ 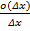 ,
, 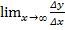 =A+
=A+ 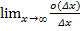 =A, y’(x0)=A. Δy0=y’(x0)+o(
=A, y’(x0)=A. Δy0=y’(x0)+o( 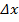 )
)
Достаточность-считается,что в т. x0 существует конечная производная. Надо доказать, что в x0 функция дифференцируема. По определению производной 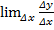 =f’(x), тогда
=f’(x), тогда 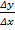 – y’(x0)=α(
– y’(x0)=α( 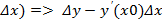 = α(
= α( 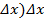 ,
, 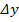 =y’(x0)*
=y’(x0)* 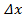 +o(x)
+o(x)
Дифференциал функции.
Дифференциалом функции dy в точке x0 называется главное приращение функции в этой точке dy=y’(x)*dx
Правила дифференцирования суммы, разности, произведения частного(теорема27).
Пусть функции u(x) и g(x) дифференцируемы в точке x. Тогда сумма, разность, произведение, частное(при условии, что знаменатель ≠0 в точке x) этих функций также дифференцируемы. При этом справедливы формулы:
1. 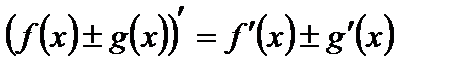 .
.
2. 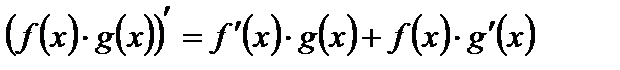 .
.
3. 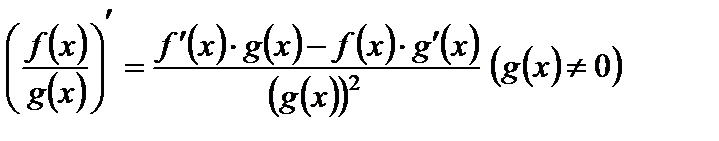 .
.
Дифференцирование обратной функции(теорема28)
Пусть функция y=f(x) дифф. в точке x0 и пусть в окрестности этой точки y=f(x) имеет обратную функцию x=f-1(y). Тогда обратная функция дифф. в точке y0 =f(x0)(соответствует т. X0) и справедлива формула: 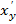 (y0)=
(y0)= 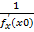 =
= 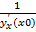
Док-во. Возьмем некоторое приращение аргумента y, т.е. 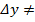 0. Тогда соответствующее приращение
0. Тогда соответствующее приращение 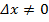 (в силу строгой монотонности обратной функции). Производная обратной функции
(в силу строгой монотонности обратной функции). Производная обратной функции 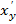 (y0)=
(y0)= 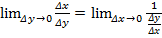 =
= 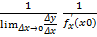 =
= 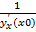
Производные показательной и обратных тригонометрических функций.
1. y=ax (a>0, a≠0, x (-∞, +∞)) x=logay обратная функция. y’=[ax]x’= 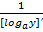 =
= 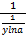 =ylna=axlna
=ylna=axlna
2. y=arcsinx (x [-1, 1], y [ 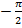 ,
,  ]) x=siny, y’=[arcsinx]’=
]) x=siny, y’=[arcsinx]’= 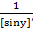 =
= 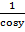 . Используя основное тригонометрическое тождество: sin2y+cos2y=1 => cosy=+-
. Используя основное тригонометрическое тождество: sin2y+cos2y=1 => cosy=+- 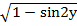 , cosy=
, cosy= 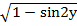 , тк y [
, тк y [ 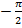 ,
,  ].
]. 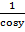 =
= 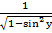 =
= 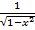 . По аналогии ищутся другие производные.
. По аналогии ищутся другие производные.
3. Y=arctg x; (x (-∞, ∞), y ( 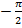 ,
,  )), x=tg x. y’=[arctg x]’=
)), x=tg x. y’=[arctg x]’= 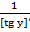 =cos2y=(1+tg2y=
=cos2y=(1+tg2y= 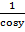 )=
)= 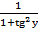 =
= 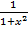 . [arctg x]’=
. [arctg x]’= 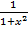 .
.
Правило дифференцирования сложной функции(теорема29).
Рассмотрим сложную функцию вида y=f(g(x)). Пусть функция g(x) дифференцируема в точке x0 , а функция f(g) дифференцируема в точке g0=g(x). Тогда сложная функция y=f(g(x)) дифференцируема в точке x0 , при этом справедлива формула 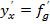 *
* 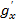 (без доказательства).
(без доказательства).
Логарифмическая производная.
Пусть функция y=f(x) дифференцируема в точке x и положительна в ней. Тогда имеет смысл равенство ln y=ln f(x), (ln y)’=(ln(f(x)))’ => 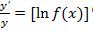 => y’=y(ln f(x))’; логарифмическая производная применяется при вычислении производной функции вида y=
=> y’=y(ln f(x))’; логарифмическая производная применяется при вычислении производной функции вида y=