Разложение вектора по ортам координатных осей

Матрицы

Матрицей называется прямоугольная таблица чисел, состоящая из m-строк одинаковой длины и n-столбцов. Говорят что это матрица размером mxn и ее записывают в виде: 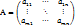. Более кратко матрицу обозначают А=(аij), где i-нмер строки, j-номер столбца.

Матрица у которой m=n называется квадратной

Если у матрицы все элементы, кроме эл. стоящих на главной диагонали, равны 0, то она называется диагональной. Диагональная матрица должна быть квадратной.

Матрица вида 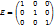называется единичной матрицей.

Кв. матр. наз. треугольной, если все элементы расположены по одну сторону от главной диагонали равны 0.

Матр. у которой все элементы равны 0 наз. нулевой.

Матр. вида А=(а₁₁...а_1n) наз. матрица-строка

Матрица полученная из данной заменой каждого ее строки на столбец с тем же номером наз. матр. транспонированной к данной

Операция умн. 2-х матриц вводится, только для случая, когда число столбцов 1-й матр. равно числу строк 2-й матр.

Определители

Кв. матрица А порядка n можно поставить в соответствие число называемое ее определителем. Определитель обозначается: Δ, |А|, detA (детерминант)

Определитель 4, 5… порядка можно вычислить только с помощью св-в определителя.

Св-во определителя:

1.Определитель имеющий 2 одинаковых ряда равен 0.

2.При перестановке 2-х параллельных рядов опред. изменит знак.

3.Умножение всех элем. одного ряда на любое число k равносильно умножению опред. на это число.

4.Если все элем. одного ряда равны 0, то и сам опред. тоже равен 0

5.Если элем. 2-х рядов опред. пропорциональны то опред. равен 0

6.Если элем. какого либо ряда представляют собой сумму 2-х слагаемых, то опред. можно разбить на сумму 2-х соответствующих опред.

7.Опред. не изменится если к элементам некоторого ряда прибавить элементы другого параллельного рада умноженные на любое число k.

Минором элемента a_­­ij опред. n-ого порядка наз. опред. (n-1)-ого порядка полученный из данного путем вычеркивания i строки и jстолбца.

Алгебраическим дополнением эл. а_ij наз. минор взятый со знаком +, если сумма i+j=четное число. И со знаком - , если сумма i+j=не четное число.

1. Разложение определителя по рядам. Опред. равен сумме произведений эл. некоторого ряда на соответствующие им алгебраические дополнения.

2. Сумма произведений какого-либо ряда определителя на соответствующие алгебраические дополнения параллельного ряда равны 0

Система линейных уравнений

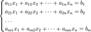
Метод Крамера: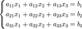

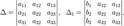
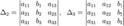
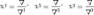
Метод обр. матриц: А^-1=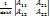

Метод Гаусса: Приводим к треугольному виду. Строки можно менять местами; строки можно складывать и вычитать; строку можно умножать на любое число и прибавить к другому. Ранг матр. – это кол-во не нулевых строк в Δ матр. rangA=rangB=n – ед. решение; rangA=rangB≠n – имеет множество решений.

Вектор

Вектор – направленный отрезок прямой

Коллинеарные вектора – если они расположены на одной прямой или параллельно

Равенство векторов: два вектора наз. равными если их модули и направления равны.

Единичный вектор – это вектор длина которого равна 1

Компкланарные векторы – если они расположены в одной плоскости или в параллельных плоскостях

Операции над векторами

1. Сложение, вычитание. Правило многоугольника (конец 2 к началу 1)

2. Умножение вектора на число: |b|=λ|a|

Свойство сложения и умножения на число:

a+b=b+a; (a+b)+c=a+(b+c); λ₁*(λ₂*a)= λ₁*λ₂*a; λ(a+b)=λa+λb

Вектороное произведение

axb=-bxa; λ(axb)=(λa)xb=ax(λb); (a+b)xc=(axc)+(bxc); axb=0 a||b

axb=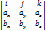

S=|axb|; V=|(axb)*c| - см. произв. V_пир=1/6|(axb)*c|

Смешанное произведение – число равное скалярному произведению вектора axb и c.

Если 3 вектора компланарны то их смешенное произведение = 0

Аналитическая геометрия

Плоскости

М₀(х₀;y₀;z₀) N{A;B;C}

A*(x+x₀)+B*(y+y₀)+C*(z+z₀)=0 – уравнение плоскости

М₁(х₁;y₁;z₁) М₂(х₂;y₂;z₂) М₃(х₃;y₃;z₃)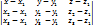

Отрезки a,b,c: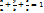

Ax+By+Cz+D=0 – общее уравнение плоскости

Угол между 2-мя плоскостями cosα=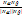

α||β 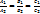; α_|_β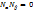

расстояние от точки до плоскости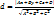

Прямая

М₁(х₁;y₁;z₁) М₂(х₂;y₂;z₂)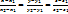

М₀(х₀;y₀;z₀) S{m;n;p}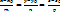

S=N_αxN_β

Угол между прямой и плоскостью: sinα=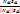

Точка пересечения прямой и плоскости: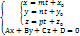

Кривые 2-ого порядка

Окр. Радиуса R с центром в точке M₀ наз. множество всех точек М плоскости удовлетворяющих условию: М₀М=R

(x-x₀)²+(y+y₀)²=R² – каноническое уравнение окружности

Эллипс – множество всех точек плоскости, для которых сумма расстояний от 2-х данных точек, называемых фокусами, постоянно иона больше, чем расстояние между фокусами.

Гипербола – множество всех точек плоскости для которых модуль разности растояний от 2-х данных точек наз. фокусами есть величина постоянная и меньшая чем расстояние между фокусами.

Парабола – множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от главной точки наз. фокусом и от длинной прямой наз. директрисой

Матанализ

Пределы

Ф-ция наз. б.б. если для любого числа М существует такое число δ>0, что для всех х удовлетворяющих неравенству 0<|x-x₀|<δ выполняется неравенство вида |f(x)-A|<ε. Lim_x->x0f(x)=∞

Бесконечно большой величиной наз. переменная величина, абсолютноезначениекоторой неограниченно возрастает.

Ф-ция наз. б.м. при х->x₀, если предел этой ф-ции = 0

Св-во б.м.ф.: алгебраическая сумма б.м.ф. есть б.м.ф.; произведение ограниченной ф-ции на б.м.ф. есть б.м.ф.; произведение 2-х б.м.ф. есть б.м.ф.; если ф-ция f(x)- б.м.ф., то ф-ция1/f(x)- есть б.б.ф., т.е. ф-цияобратная б.м.ф. есть б.б.ф. и наоборот.

Производная

(a)`=0

(x)`=1

(uⁿ)`=n*u<sup>n-1</sup>*u`

(a^u)`=a<sup>u</sup>*lna*u`

(e^u)`=e<sup>u</sup>*u`

(log_au)`=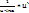

(lnu)`=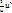

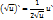
(sinu)`=cosu*u`

(cosu)`=-sinu*u`

(tgu)`=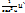

(ctgu)`=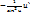

(arcsinu)`=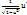

(arccosu)`=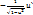

(arctgu)`=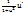

(arcctgu)`=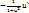

Правило дифференцирования

(с*u)`=c*(u)`

(u±v)`=u`±v`

(u*v)`=u`v+uv`

( )`=

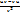
( )`= *(u)`

Матрицы

Матрицей называется прямоугольная таблица чисел, состоящая из m-строк одинаковой длины и n-столбцов. Говорят что это матрица размером mxn и ее записывают в виде: 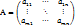. Более кратко матрицу обозначают А=(аij), где i-нмер строки, j-номер столбца.

Матрица у которой m=n называется квадратной

Если у матрицы все элементы, кроме эл. стоящих на главной диагонали, равны 0, то она называется диагональной. Диагональная матрица должна быть квадратной.

Матрица вида 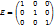называется единичной матрицей.

Кв. матр. наз. треугольной, если все элементы расположены по одну сторону от главной диагонали равны 0.

Матр. у которой все элементы равны 0 наз. нулевой.

Матр. вида А=(а₁₁...а_1n) наз. матрица-строка

Матрица полученная из данной заменой каждого ее строки на столбец с тем же номером наз. матр. транспонированной к данной

Операция умн. 2-х матриц вводится, только для случая, когда число столбцов 1-й матр. равно числу строк 2-й матр.

Определители

Кв. матрица А порядка n можно поставить в соответствие число называемое ее определителем. Определитель обозначается: Δ, |А|, detA (детерминант)

Определитель 4, 5… порядка можно вычислить только с помощью св-в определителя.

Св-во определителя:

1.Определитель имеющий 2 одинаковых ряда равен 0.

2.При перестановке 2-х параллельных рядов опред. изменит знак.

3.Умножение всех элем. одного ряда на любое число k равносильно умножению опред. на это число.

4.Если все элем. одного ряда равны 0, то и сам опред. тоже равен 0

5.Если элем. 2-х рядов опред. пропорциональны то опред. равен 0

6.Если элем. какого либо ряда представляют собой сумму 2-х слагаемых, то опред. можно разбить на сумму 2-х соответствующих опред.

7.Опред. не изменится если к элементам некоторого ряда прибавить элементы другого параллельного рада умноженные на любое число k.

Минором элемента a_­­ij опред. n-ого порядка наз. опред. (n-1)-ого порядка полученный из данного путем вычеркивания i строки и jстолбца.

Алгебраическим дополнением эл. а_ij наз. минор взятый со знаком +, если сумма i+j=четное число. И со знаком - , если сумма i+j=не четное число.

1. Разложение определителя по рядам. Опред. равен сумме произведений эл. некоторого ряда на соответствующие им алгебраические дополнения.

2. Сумма произведений какого-либо ряда определителя на соответствующие алгебраические дополнения параллельного ряда равны 0

Система линейных уравнений

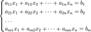
Метод Крамера: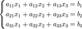

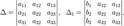
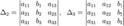
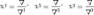
Метод обр. матриц: А^-1=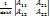

Метод Гаусса: Приводим к треугольному виду. Строки можно менять местами; строки можно складывать и вычитать; строку можно умножать на любое число и прибавить к другому. Ранг матр. – это кол-во не нулевых строк в Δ матр. rangA=rangB=n – ед. решение; rangA=rangB≠n – имеет множество решений.

Вектор

Вектор – направленный отрезок прямой

Коллинеарные вектора – если они расположены на одной прямой или параллельно

Равенство векторов: два вектора наз. равными если их модули и направления равны.

Единичный вектор – это вектор длина которого равна 1

Компкланарные векторы – если они расположены в одной плоскости или в параллельных плоскостях

Операции над векторами

1. Сложение, вычитание. Правило многоугольника (конец 2 к началу 1)

2. Умножение вектора на число: |b|=λ|a|

Свойство сложения и умножения на число:

a+b=b+a; (a+b)+c=a+(b+c); λ₁*(λ₂*a)= λ₁*λ₂*a; λ(a+b)=λa+λb

Разложение вектора по ортам координатных осей

|a| - длина вектора

cosα , cosβ , cosγ – направляющие косинусы; cosα= 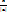, cosβ= 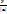, cosγ=