Вероятность произведения двух независимых событий равна
B. произведению вероятности одного из событий на вероятность второго события;
Укажите, какие из перечисленных событий достоверные:
B. «появление не более 18 очков при бросании трех игральных костей»;
C. «наугад выбранное трехзначное число не больше 1000»;
D. «из ящика с белыми шарами достают белый шар»;
Сумма двух событий A и B - достоверное событие, произведение этих событий невозможное событие. Эти два события являются:
A. противоположными;
По какой формуле вычисляется вероятность противоположного события , если известна вероятность P(A) события A?
C.
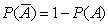 |
Вероятность суммы двух несовместимых событий A и B равна
D.
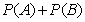 |
Вероятность суммы двух совместимых событий A и B равна
B.
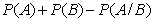 |
Вероятность появления хотя бы одного из событий , независимых друг от друга, равн
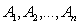 |
C.
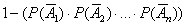 |
Безусловной вероятностью события А называется
D. вероятность события А, вычисленная без дополнительных условий.
Можно ли теорему умножения записать в виде:
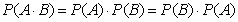 |
A. да;
Будет ли вероятность суммы несовместимых событий равна единице?
A. зависит от природы случайных событий;
Если событие невозможное, то вероятность
B. равна 0;
Относительной частотой случайного события А называется величина, равная
A. отношению числа случаев, благоприятствующих событию А к общему числу равновозможных, несовместных событий;
Укажите классическое определение вероятности случайного события А:
A. отношение числа случаев, благоприятствующих событию А к общему числу равновозможных, несовместных событий;
Укажите статистическое определение вероятности случайного события А:
C. отношение числа испытаний, в которых реализуется событие А, к общему числу испытаний;
Укажите диапазон значений, которые может принимать вероятность случайного события А:
B.
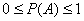 |
Случайным событием называется событие, которое…
B. может произойти или не произойти при многократном повторении испытаний;
Укажите формулировку теоремы сложения вероятностей:
D. вероятность совместного появления независимых событий равна сумме их вероятностей.
Укажите формулировку теоремы умножения вероятностей:
B. вероятность совместного появления независимых событий равна произведению их вероятностей;
Какая из формул нахождения вероятности произведения верна?
A.
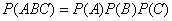 |
Статистика показывает, что вероятность рождения мальчика равна 0,516. Какова вероятность того, что новорожденный ребенок окажется девочкой?
B. Р=0,484;
На приеме у участкового врача в течение недели побывало 35 пациентов, из которых 5 пациентам был поставлен диагноз – язва желудка. Определите относительную частоту появления на приеме пациента с заболеванием желудка.
C. 5/35;
Укажите классическое определение вероятности наступления события А:
A отношение числа случаев, благоприятствующих событию А, к общему числу равновозможных несовместных событий;
D отношение числа испытаний, в которых реализуется событие А, к общему числу испытаний.
