Построение корреляционной таблицы
Построим корреляционную таблицу:
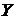 ╲ ╲ 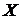 | [3,82; 4,29) 4,055 | [4,29; 4,76) 4,525 | [4,76; 5,23) 4,995 | [5,23; 5,7) 5,465 | [5,7; 6,17) 5,935 | [6,17; 6,64) 6,405 | [6,64; 7,11) 6,875 | [7,11; 7,58) 7,345 | [7,58; 8,05) 7,815 | [8,05; 8,52) 8,285 | 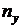 | 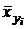 | 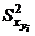 |
| [27,72;42,5) 35,11 | 4,3488 | 0,05177 | |||||||||||
| [42,5;57,28) 49,89 | 4,9227 | 0,02876 | |||||||||||
| [57,28;72,06) 64,67 | 5,4374 | 0,03822 | |||||||||||
| [72,06;86,84) 79,45 | 5,9663 | 0,01374 | |||||||||||
| [86,84;101,62) 94,23 | 6,405 | ||||||||||||
| [101,62;116,4) 109,01 | 6,8323 | 0,01826 | |||||||||||
| [116,4;131,18) 123,79 | 7,251 | 0,3534 | |||||||||||
| [131,18;145,96) 138,57 | 7,345 | ||||||||||||
| [145,96;160,74) 153,35 | 7,9717 | 0,04909 | |||||||||||
| [160,74;175,52) 168,13 | 8,285 | ||||||||||||
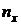 | |||||||||||||
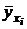 | 35,11 | 39,3329 | 52,1638 | 64,67 | 78,4647 | 94,23 | 111,4733 | 127,8209 | 153,35 | 165,174 | |||
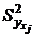 | 44,5813 | 28,4371 | 13,5923 | 24,272 | 30,3401 | 43,3286 | 34,9517 |
2.3. Проверка однородности дисперсий случайных величин 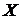 и
и 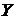 по критерию Бартлетта
по критерию Бартлетта
Проверим однородность дисперсий случайных величин 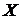 и
и 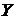 по критерию Бартлетта. Проверим нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой.
по критерию Бартлетта. Проверим нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой.
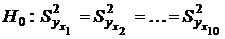 .
.
Найдем дисперсию воспроизводимости 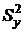 по формуле (17).
по формуле (17).
В качестве критерия проверки нулевой гипотезы об однородности дисперсий примем критерий Бартлетта (18).
Критическую точку 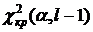 находим по уровню значимости
находим по уровню значимости  и числу степеней свободы
и числу степеней свободы 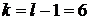 :
: 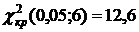 .
.
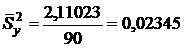 ;
; 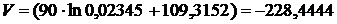 ;
;
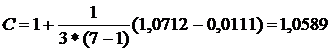 ;
; 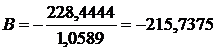 .
.
Сравним 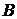 и
и 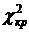 :
: 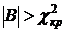 – гипотеза отвергается.
– гипотеза отвергается.
Проверим однородность дисперсий случайной величины 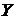 :
:
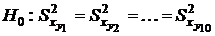 .
.
Найдем дисперсию воспроизводимости 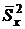 :
:
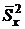 =
= 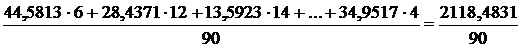 =
=
=23,5387;
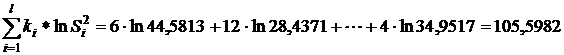 ;
;
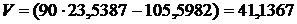 ;
;
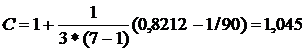 ;
;
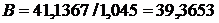
Сравним 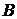 и
и 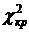 :
: 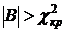 – гипотеза отвергается.
– гипотеза отвергается.
Итак, обе величины 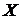 и
и 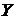 имеют неоднородные дисперсии, т.е. экспериментальные данные получены некорректно. Вообще говоря, мы не имеем права продолжать работу по статистической обработке. Но в учебных целях перейдем к следующему пункту.
имеют неоднородные дисперсии, т.е. экспериментальные данные получены некорректно. Вообще говоря, мы не имеем права продолжать работу по статистической обработке. Но в учебных целях перейдем к следующему пункту.
Построение линейной регрессионной модели
По формуле (5) определим выборочный коэффициент корреляции, для чего сначала вычислим
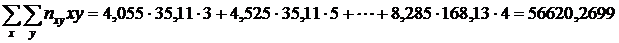 ,
,
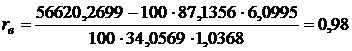 .
.
Так как полученный коэффициент 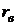 равен 0,98, то линейная связь между признаками
равен 0,98, то линейная связь между признаками 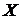 и
и 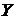 весьма высокая.
весьма высокая.
Найдем выборочные коэффициенты регрессии:
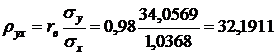 ;
; 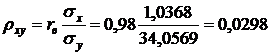 .
.
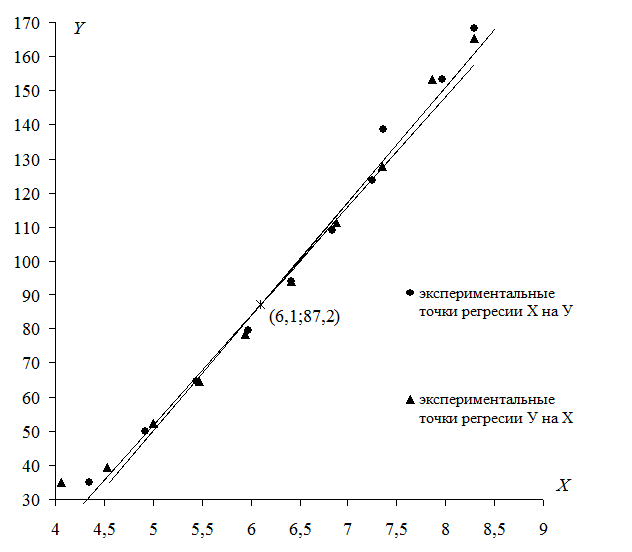
Следовательно, выборочное уравнение прямой линии регрессии 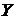 на
на 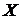 (6) имеет вид
(6) имеет вид
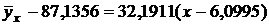 ;
; 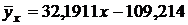 .
.
Выборочное уравнение прямой линии регрессии 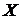 на
на 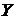 (7) имеет вид
(7) имеет вид
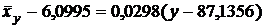 ;
; 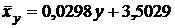 .
.
Точкой пересечения двух прямых является точка 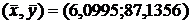 .
.
| |
| |
|
Точечная и интервальная оценки коэффициента корреляции генеральной совокупности
Точечная оценка:  ,
, 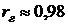 ;
;
Интервальная оценка (8):
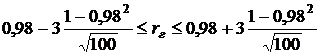 ;
;
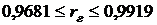 .
.
Проверка гипотезы о значимости выборочного коэффициента корреляции
Проверим нулевую гипотезу о равенстве нулю генерального коэффициента корреляции  при конкурирующей гипотезе
при конкурирующей гипотезе  .
.
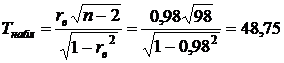 .
.
Найдем  , где
, где  – уровень значимости,
– уровень значимости, 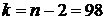 – число степеней свободы;
– число степеней свободы; 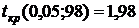 . Сравним
. Сравним  и
и 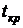 :
:  – нулевую гипотезу отвергаем, выборочный коэффициент значимо отличается от нуля, т.е.
– нулевую гипотезу отвергаем, выборочный коэффициент значимо отличается от нуля, т.е. 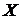 и
и 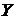 линейно коррелированы.
линейно коррелированы.
Вычисление корреляционных отношений
Вычислим по формуле (14) корреляционное отношение  .
.
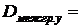
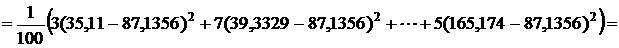
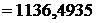 ;
;
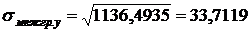 ;
;
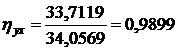 .
.
Аналогично находим  по формуле (15).
по формуле (15).
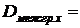
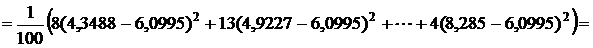
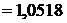 ;
;
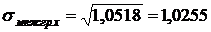 ;
;
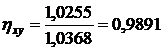 .
.
Следовательно, 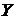 связан с
связан с 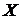 корреляционной зависимостью.
корреляционной зависимостью.
