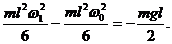Отметим, что мощность силы в этом случае вычисляется по формуле

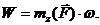(97)

4.4.4. Теорема об изменении кинетической энергии.

Выведем формулы, выражающие эту теорему. Запишем уравнения движения точек механической системы в виде

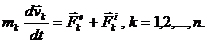
Умножим каждое из этих уравнений скалярно на дифференциал радиуса-вектора соответствующей точки 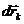и полученные уравнения почленно сложим

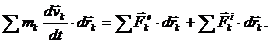(98)

Преобразуем выражение в левой части (98), пользуясь свойствами дифференциала:

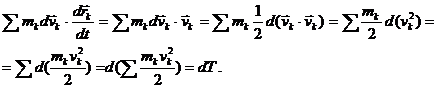
Здесь Т – кинетическая энергия механической системы. Учитывая также, что элементарная работа внешних и внутренних сил выражается по формулам

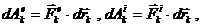
из (98) получим

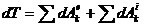(99)

Формула (99) выражает теорему об изменении кинетической энергии механической системы в дифференциальной форме: дифференциал от кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.

При решении практических задач такая форма записи теоремы обычно не используется. Если обе части (99) проинтегрировать от начального положения механической системы до конечного, в которых кинетическая энергия соответственно равна 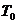и Т , и в правой части равенства поменять порядок интегрирования и суммирования, то из (99) получим

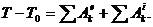(100)

Формула (100) выражает теорему об изменении кинетической энергии механической системы в интегральной форме: изменение кинетической энергии механической системы на каком-либо перемещении равно сумме работ внешних и внутренних сил, действующих на систему, вычисленных на этом перемещении.

Сделаем ряд замечаний, касающихся практического применения этой формы записи теоремы.

1. Формула (100) связывает следующие физические характеристики: массы, скорости (угловые скорости), силы и перемещения (угловые перемещения). Поэтому ее удобно использовать при решении задач, в которых перечень заданных и искомых величин соответствует этому набору.

2. Внутренние силы механической системы могут изменить ее кинетическую энергию.

3. Внутренние силы в механической системе многочисленны и, как правило, неизвестны. Поэтому формулу (100) удается использовать на практике, когда сумма работ внутренних сил системы равна нулю. Это выполняется в случае, когда тела, включенные в механическую систему, абсолютно твердые и внутренние связи идеальные.

Если теперь обе части (109) поделить на dt, то теорему можно выразить в виде

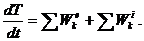(101)

Формула (101) выражает теорему об изменении кинетической энергии механической системы в форме производных: первая производная по времени от кинетической энергии механической системы равна сумме мощностей внешних и внутренних сил, действующих на систему.

Теорему в этой форме удобно использовать на практике для вычисления ускорений (угловых ускорений) тел системы.

Пример 11.

Однородный стержень длиной ОА=l=0.5 м может вращаться вокруг неподвижной оси, проходящей через точку О, оставаясь в вертикальной плоскости. В начальный момент стержень находился в нижнем вертикальном положении и ему была сообщена угловая скорость 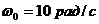(см. рис. 72). Определить угловую скорость и угловое ускорение стержня в тот момент, когда он будет проходить горизонтальное положение.

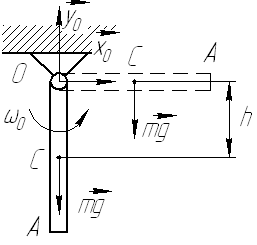
Рис 72.

Решение.

Для нахождения угловой скорости стержня в его горизонтальном положении применим теорему об изменении кинетической энергии в интегральной форме

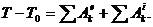(102)

Так как стержень считаем абсолютно твердым телом, то 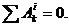Обозначим на рисунке внешние силы, к числу которых относятся сила тяжести 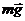и реакции опорного шарнира 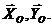Работа реакций 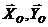равна нулю, так как точка их приложения остается неподвижной. Тогда сумма работ внешних сил равна работе силы тяжести

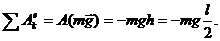
Учитывая, что стержень совершает вращательное движение вокруг оси Oz, перпендикулярной плоскости рисунка, его кинетическую энергию в начальном и конечном положениях вычислим по формулам

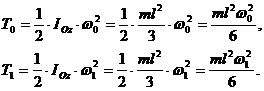
Подставим полученные выражения в формулу (102):