Метод конечных элементов (МКЭ)

Исторически возникновение МКЭ связано с идеей применения хорошо разработанных процедур для расчета статически неопределимых стержневых систем к решению континуальных задач.

Первоначально эта идея была высказана еще в 1933 году И.М. Рабиновичем, но развитие получила только в 70-х годах, с появлением ЭВМ.

Метод конечных элементов основан на мысленном представлении сплошного тела в виде совокупности отдельных конечных элементов, взаимодействующих между собой в конечном числе точек, которые в МКЭ принято называть узлами.

Система разбивается на простые конечные элементы (КЭ) напряженно-деформированное состояние которых исследуется заранее.

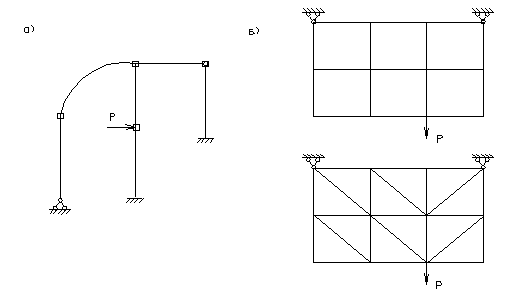
Так стержневые системы могут быть разбиты на элементы в виде прямолинейных или криволинейных стержней (например, для расчета арок) с различными условиями соединения элементов в узлах. В этом случае дискретная модель является точной копией исходной конструкции (с учетом принятых технических гипотез).

В расчетах пластин наибольшее распространение получили прямоугольные и треугольные конечные элементы. Здесь дискретная модель лишь приближенно отражает поведение исходной конструкции.

Заметим, что даже при одном и том же числе узловых точек различные схемы дискретизации исходной конструкции порождают разницу в окончательных результатах расчета. К сожалению, заранее сказать, какая из возможных схем дискретизации приведет к наименьшей погрешности расчета, невозможно.

Число степеней свободы КЭ, а в конечном итоге число неизвестных МКЭ, определяется количеством наложенных в узлах дополнительных связей.

Условия равновесия и совместности деформаций выполняются только в узловых точках - точках соединения КЭ. Однако это не значит, что общая жесткость пластины при этом резко уменьшается, поскольку зависимость между узловыми усилиями и деформациями каждого элемента рассматривается с учетом некоторых внутренних связей.

Каждый элемент является частью заменяемой среды, т.е. сплошное тело лишь условно делится на отдельные элементы конечных размеров. Выделенный элемент имеет те же физические свойства и геометрические характеристики, что и рассматриваемая конструкция в месте расположения элемента.

Все внешние силы считаются приложенными в узлах, по направлению их возможных перемещений. Вне узловые нагрузки предварительно приводятся к узловым.

При реализации МКЭ наибольшее распространение получили идеи метода перемещений, хотя имеются работы, где рассматривается метод сил и смешанный метод. Предпочтение методу перемещений отдано в основном из-за простоты выбора основной системы, составления матрицы жесткости и формирования вектора внешних нагрузок.

Разрешающее уравнение МКЭ, которое представляет собой матричную форму канонических уравнений метода перемещений, имеет вид:

[r]{Z}={P},

где: [r] - матрица жесткости сооружения в целом,

{Z}- вектор перемещений узловых точек сооружения,

{P}- вектор внешних нагрузок.

Подход к решению задачи МКЭ является единым, как для стержневых систем, так и для пластин, оболочек и объемных тел.

Дальнейшее рассмотрение МКЭ будем проводить на примере плоских стержневых систем.

Лекция 2