Лабораторная работа №3: «Регрессионный анализ»

В процессе исследования чаще всего устанавливается взаимосвязь между двумя или несколькими величинами. Например, в исследовании кинетики реакций, когда изучается зависимость концентрации продукта (или объёма или давления) от времени протекания реакции, зависимость вязкости нефтепродукта(битума) от температуры и т. п.

Рассмотрим, например, изменение вязкости битума от температуры.

Вязкость – y

Температура –х

Вязкость –(y) –величина случайная, температура – величина не случайная, её называют наблюдавшимся признаком. Эта величина всегда нам известна. Таким образом, мы изучаем связь между случайным признаком (y) и наблюдавшимся признаком (х). Анализ таких данных называется регрессионным, а графическая зависимость, получаемая при этом, называется графиком или линией регрессии

Задача исследователя заключается в оценке этой зависимости. Эта зависимость может быть прямолинейной или иметь вид другой графической зависимости (криволинейной).

Перед исследователем стоит задача описать полученную экспериментальную кривую с помощью формул. Это позволит ему предсказать значение Y при любых значениях X.

Существует два правила подбора эмпирических формул: графический (метод выравнивания) и метод наименьших квадратов.

1. Графический метод (или метод выравнивания)

Сущность метода заключается в следующем:

1. Экспериментальные точки наносят на график.

2. Строят кривую зависимости Y = f(X).

3. Ориентировочно выбирают вид формулы, описывающую эту кривую, т.е. алгебраическое выражение, объединяющее функцию с переменными Y = f(X). Эмпирические формулы являются приближенными выражениями аналитических формул.

4. Вычисляют параметры выбранной формулы.

Чаще всего между переменными y и х пытаются найти линейную зависимость. В этом случае функция цели (линия регрессии) должна иметь вид Y = a + bX.

Если зависимость криволинейная, то функция цели апроксимируется простейшими уравнениями типа: Y = aX^b; Y= a/X,

где a и b – постоянные коэффициенты.

Задача исследователя –рассчитать значение коэффициентов а и b и т.о. определить вид эмпирической формулы.

При графическом определении параметров a и b обязательно, чтобы прямая строилась на координатной сетке, у которой началом являются точки X = 0; Y = 0.

А) Пример: подобрать эмпирическую формулу следующих измерений:

Таблица 2.5

Y
X

1. Результаты измерений наносим на график.(рис. 2.1).

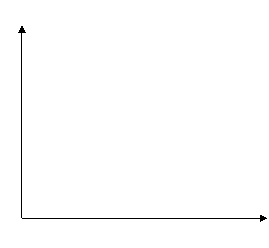Рис. 2.1. График зависимости y=f(x)

2. Точки ложатся на прямую линию, которую можно описать уравнением: y = a + bx.

3. Находим значения коэффициентов a и b. Для этого координаты крайних точек подставляем в уравнение: y = a + bx.

Имеем два уравнения: 54 = a + 7b

12 = a + 1b

4. Решаем совместно эти уравнения и определяем: a = 5; b = 7.

5. Эмпирическая формула имеет вид:

y = 5 + 7x.

Проверим достоверность полученного уравнения для точки №3:

y= 5 +7*3 = 26.

Как видно, полученное расчетное значение функции соответствует экспериментальному значению (таблица).

Графический метод выравнивания можно применять и в тех случаях, когда кривая зависимости имеет вид плавной кривой.

Б.)Например, кривая зависимости, полученная по экспериментальным данным, нанесенным на график, имеет следующий вид (рис. 2.2):

Рис. 2.2.

Данная кривая может быть описана уравнением: y = ax^b.

Экспериментальную кривую можно превратить в прямую на логарифмической сетке следующим образом:

1. Логарифмируем уравнение: y = ax^b.

lgy = lga + b∙lgx

2. Заменяем lgy на У, lgx на X и получаем уравнение прямой линии:

У = lga + b∙X,

3. Для нахождения коэффициентов a и b используем метод выравнивания и по правилам математики решаем систему двух уравнений и получаем окончательно эмпирическую формулу, описывающую искомую функцию цели.

Пример:

В результате эксперимента получены следующие результаты (табл.). Необходимо установить эмпирическую зависимость и найти уравнение, описывающее эту зависимость.

Таблица 2.6

x
y

1. Строим график зависимости y =f(x).

2. Полученная зависимость может быть описана уравнением:

y=ax^b

3. Определяем коэффициенты a и b методом выравнивания. Для этого логарифмируем уравнение, подставляем координаты крайних точек и решаем систему из двух уравнений относительно «а» и «b»:

4. lgy = lga + b∙lgx

lg20 =lga + b*lg1

lg90 = lga + b*lg7

В результате расчетов получаем <a> =20, <b> =0,77

Таким образом ,уравнение зависимости y =f(x) имеет вид:

Y = 20x^0,77

2. Метод наименьших квадратов

Для определения коэффициентов a и b в эмпирических формулах, можно использовать метод наименьших квадратов:

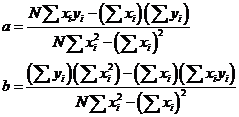
где y_i – экспериментальное значение, соответствующее x_i$

N – число измрений.

Содержание и последовательность выполнения работы:

1. Ознакомиться с содержательной постановкой задачи.

2. Получить задание (приложение 4), дать оценку результатам (построить график зависимости, определить вид формулы и найти параметры выбранной формулы)

Планирование эксперимента

3.1. Лабораторная работа №4: ««Классическое планирование однофакторного эксперимента»

1. Теоретическая часть

Эксперимент - научно-поставленный опыт в точно контролируемых условиях.

Основная цель эксперимента проверка и подтверждение гипотезы.

Прежде, чем приступить к работе выдвигается рабочая гипотеза;

-определяется цель исследования.

-задачи исследования.

Эксперимент осуществляется в соответствии с планом.

Типы планов:

1.Класический план.

2.Рандомизированный план.

3.Математическое планирование.

В процессе исследования экспериментатор выясняет зависимость определенного признака (свойства) от других переменных или факторов. Например, зависимость октанового числа топлива от количества антидетонационной присадки и т.п.

Пусть интересующее нас свойство (y) объекта зависит от нескольких (n) независимых переменных (x₁,x₂...x_n)

y-свойство (признак) изучаемое в исследовании.

x₁,x₂...x_n (x_i)- факторы, переменные, влияющие на изучаемое свойство.

n-количество переменных

Итак, мы хотим выяснить характер этой зависимости, о которой мы имеем лишь общее представление, т.е. y=f(x₁,x₂...x_n)-эта зависимость называется «функция отклика».

Функция цели (y) - может зависеть от одного или нескольких факторов.

В зависимости от этого эксперимент бывает: однофакторным или двух (много) факторным.

y=f(x) – однофакторный эксперимент

y=f(x₁,x₂...x_n) – одно(много)факторный эксперимент.

2. Классическое планирование однофакторного эксперимента

Классический план называют также последовательным, т.к. в ходе эксперимента последовательно изменяют величину варьируемого фактора в заданных пределах.

Порядок планирования:

1. Устанавливают верхнее или нижнее значение фактора, т.е. один из его предельных уровней (x_min,x_max)

2. Назначают интервал варьирования(∆x)

3. Составляют план-матрицу эксперимента. Определяют последовательность проведения опытов, причем в каждом последующем опыте изменяют значения фактора на величину согласно принятому интервалу варьирования.

4. Проводят эксперимент.

5. Заполняют рабочий журнал.

6. Проводят обработку результатов эксперимента, используя статистические, графические и математические методы.

Пример:

Тема: изучение детонационной стойкости бензина в присутствии антидетонаторов нового типа.

Рабочая гипотеза:

Марганцевые антидетонаторы (МА) в 300 раз менее токсичны, чем ТЭС; хорошо растворимые в бензине; практически не растворимы в воде.

Возможность замены ими ТЭС, если эффективность не ниже, чем у свинцовых.

Цель: Изучение влияния антидетонационной присадки (МА) на изменение октанового числа крекинг-бензина прямой перегонки.

Задачи:

1.Изучить зависимость ОЧ от количества добавляемой присадки (г/кг).

2.Определить оптимальные количество добавки МА.

Основные характеристики:

y – октановое число (ОЧ) функция цели.

x - марганцевый антидетонатор (МА – фактор варьируем)

Нижний уровень фактора –( x_min)=0,5 г/кг

Интервал варьирования – ∆x=0,5 г/кг

Верхний уровень фактора – (x_max)=3,5 г/кг

Составим план матрицу эксперимента.

Таблица 3.1

№ опыта	X	Y	Y*
	МА,%	ОЧ, мм	ОЧ, мм
	- 0,5 1,0 1,5 2,0 2,5 3,0 3,5

Y^*-заполняется после эксперимента.

Проводим эксперимент

а). подбираем материалы и оборудование .

б). описываем подробно ход эксперимента.

Заполняем таблицу.

Строим график зависимости ОЧàf(MAD). yàf(x)

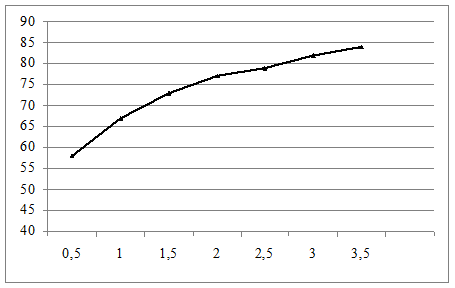
Рис.3.1. График зависимости октанового числа (ОЧ) от

количества МАД

Как видно из графика, зависимость может быть описана уравнением:

Y=ax^b

После подбора коэффициентов методом выравнивания получаем математическое выражение искомой зависимости y=73x^0.12.

3.2. Лабораторная работа №5: «Классическое планирование двухфакторного (многофакторного) эксперимента»

1. Порядок планирования

1.Устанавливают значение обоих факторов на определенном уровне.

2.Один фактор фиксируют x₂ на принятом уровне, для второго фактора (x₁) назначают интервал варьирования ∆x.

3.Составляют план эксперимента, в котором изменяют скачками один фактор в соответствии с принятым интервалом варьирования, а другой фактор остается неизменным.

4.Проводят серию опытов. В результате получают функцию цели в зависимости от одной переменной при постоянном уровне второй, т.е. y=f(x₁) при x₂=const.

5.Фиксируют первый фактор x₁=const, а второй - x₂ меняют в соответствии с принятым интервалом варьирования.

6.Проводят вторую серию опытов и в результате получают значение функции цели в зависимости от второго фактора при постоянном уровне первого, т.е. y=f(x₂) при x₁=const.

Таким образом, классический план двухфакторного( многофакторного) эксперимента. является суммой последовательных однофакторных экспериментов.

Классический план двух(много)факторного эксперимента может быть:

а)частичным.

б)полным.

Частичным называется тогда, когда проводится только две серии опытов.

В каждой серии фактор стабилизируют только на одном уровне

По результатам эксперимента можно построить графическую иллюстрацию для функции цели всего из двух кривых.

	Y

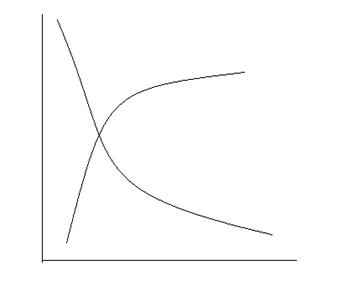
y₁=f(x₁)приx₂=cost

y₂=f(x₂) при x₁=const

	X

Полный план.

В случае полного плана каждый фактор стабилизируют на всех уровнях.

По результатам можно построить два графика зависимости с пятью кривыми

Y

	X2

		X1
	X

Полный классический план может осуществляться только для воспроизводимых экспериментов. Классические планы эксперимента являются наиболее популярными

Пример:

Тема: оптимизация процесса получения бензиновой фракции при каталитическом крекинге гудрона.

Цель: изучить влияние температуры (Т,С) и давления(Р) на выход бензиновой фракции.

Задачи:

1.Определить зависимость выхода бензина от температуры.

2.Определить зависимость выхода бензина от давления.

3.Определить оптимальные параметры процесса.

Основные характеристики:

Y-выход бензина, % масс.;

X₁-температура Т; от 450ᵒ до 530ᵒ ((∆x₁=20⁰С);

X₂-давление, МПа; от 0,06 до 0,14 (∆x₂=0.02 МПа)

Составляем план-матрицу эксперимента.

Планируем опыты №1 - №5 при постоянном уровне фактора Х₂= 0,10 Мпа , при этом фактор Х₁ меняем в каждом опыте с принятым интервалом варьирования = 20⁰С. ( I серия опытов).

II серия опытов планируется при постоянном уровне фактора Х₁=490⁰С, фактор Х₂ меняем с принятым для него интервалом варьирования =0,02Мпа.

Проводим эксперимент в соответствии с разработанным планом. Результаты заносим в таблицу.

Таблица 3.2

План-матрица эксперимента

N опыта	X1	X2	Y
	T,ᵒc	P,МПа	Б,%
5		0,10 0,10 0,10 0,10 0,10 0,06 0,08 0,10 0,12 0,14

По результатам эксперимента строим графики зависимостей

1. Y=f(T,ᵒc) при P=0.10 МПа

2.Y=f(P) при T=490°С

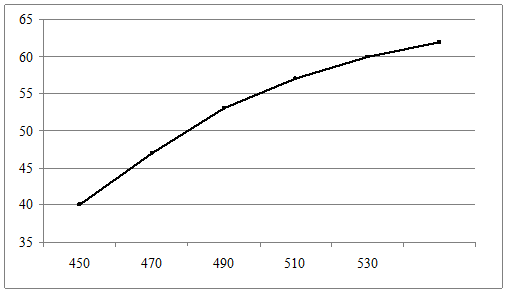
Рис.3.2. График зависимости.y=f(Tᵒ)

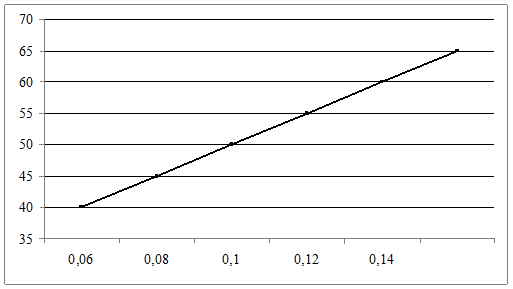
Рис.3.3. График зависимости выхода бензина от давления. Y=a+bx

Для каждого полученного графика определяется вид кривой, определяются её параметры и устанавливаются математические модели изучаемого процесса.