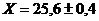Лабораторная работа №2: «Оценка достоверности результатов измерений (отбрасывание малоправдоподобных данных)»

1. Содержательная постановка.

В тех случаях, когда среди результатов измерений одно значение существенно отличается от всех остальных или от среднего значения, необходимо принять решение, следует ли вообще учитывать это аномальное значение или отбросить его как малоправдоподобное. Для принятия решения можно воспользоваться одним из 4^Х методов.

2. Метод «четырех » :

В этом методе используется введенное понятие о среднем отклонении .

Порядок проверки.

1. Вычисляем среднее арифметическое серии (Х) и среднее отклонение (Д)

2. Находим сомнительный результат Х_сомн

3. Отбрасываем малоправдоподобное значение и вычисляем по оставшимся результатам данной серии новое среднее значение 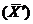и новое среднее отклонение .

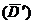4. Вычисляем значение .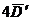

5. Определяем разницу между сомнительным значением и новым средним .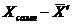

6. Если результат сомнительного значения отличается от нового среднего значения более, чем на 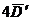, то его отбрасывают как малоправдоподобный.

Этот метод обеспечивает приблизительно 99%-ую вероятность того, что отбрасывание подозрительного значения оправдано (если число данных ).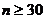

Столь высокий доверительный уровень (99%) нередко совсем не обязателен и его можно применять и при меньшем числе измерений.

Пример:

Имеем следующую серию результатов измерений:

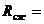26,2; 26,0; 27,5; 25,6; 25,2; 24,9.

1. Сомнительным результатом является значение 27,5.

2. Определяем среднее арифметическое без величины 27,5 и среднее отклонение .

Таблица 2.3

26,2	0,6
26,0	0,4
25,6
25,2	0,4
24,9	0,7

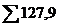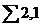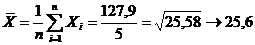
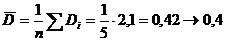
Находим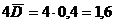

3. Находим разницу между 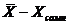, т.е. 25,6-27,5=1,9

4. Сравниваем значение 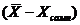с величиной 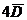, т.е 1,9 > 1,6 и делаем вывод. Так как разница 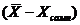больше, чем 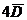, то сомнительное значение 27,5 следует отбросить.

3. Метод « »: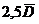

Этот метод можно принять, когда экспериментальная ошибка равна 5%. Порядок проверки такой же, что и для метода .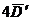

4. Использование Q-критерия:

Этим методом предпочитают пользоваться в тех случаях, когда имеется не более десяти результатов измерений. Разность между проверяемым значением и минимально отличающимся от него другим значением рассматриваемой серии измерений (по абсолютной величине) делят на ее размерах (W-максимальную разность значений серии):

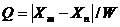(8)

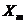- сомнительный результат;

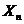- следующий после сомнительного по величине результат.

Результат деления сравнивают с указанными ниже стандартными значениями: Q -критерия

Таблица 2.4

n	Q	n	Q
	0,94		0,51
	0,76		0,47
	0,64		0,44
	0,56		0,41

Если частное от деления превышает соответствующее Q-значение, проверяемый результат измерения отбрасывают.

Порядок проверки:

1. Выбираем сомнительное значение из серии измерений X_m-

2. Находим значение, минимально отличающееся от сомнительного результата -Xn.

3. Вычисляем разницу между ними ,т.е. Х_m.-Х_n..

4. Рассчитываем размах W- максимальную разность значений серии

W = X_max - X_min. (9)

5. Определяем расчетное значение Q-критерия (Q_р)

Q_р= X_m - X_n/W (10)

6. Сравниваем расчетное значение Q_р с табличным значением Q_табл.

7. Если – Q_р превышает Q_табл., то проверяемый результат отбрасываем как малодостоверный.

Пример использования:

Для рассматриваемой серии измерений (см. 2.2.1.1.)

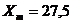(сомнительный результат).

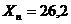(минимально отличающийся результат от сомнительного).

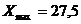(максимальное значение серии).

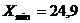(минимальное значение серии).

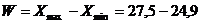(размах).

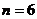(число опытов).

Находим значение Q-критерия по формуле:

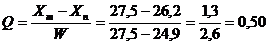
Сравниваем полученное значение Q-критерия с табличным значением для 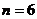. (Q_табл=0,56).

Т.к. Q_р <Q_табл, то результат 27,5 нельзя отбрасывать.

Таким образом, значение измеряемой величины определяем как среднее арифметическое значение из всех 6 измерений с учётом средней ошибки всех измерений: Х= 25,9 +_0,7

5. Использование t-критерия:

Этот метод применяется при количестве измерений 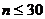и с учетом стандартного отклонения для определённой надёжности.

Порядок проверки:

1. Отбрасываем сомнительный результат.

2. Для оставшихся значений определяем среднее значение и стандартное отклонение .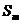

3. Из таблицы «значение критерия Стьюдента» находим величину поправочного коэффициента t при необходимом доверительном интервале и 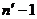, где

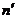- число результатов опытов без сомнительного значения.

4. Рассчитываем значение измеряемой величины:

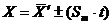(11)

5. Любой результат, выходящий за пределы этого значения, можно отбросить как малоправдоподобный.

Пример использования метода t-критерия:

Для рассматриваемого примера имеем:

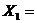26,2; 26,0; 27,5; 25,6; 25,2; 24,9;

Расчет ведем для вероятности 95,0%.

Сомнительным считаем результат .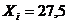

1. Рассчитываем без сомнительного:

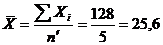
2. Определяем S и S_m.

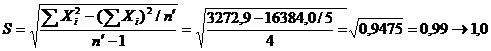
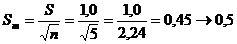
3. Находим значение коэффициента t из табл. 1 (приложение 1) «Значение коэффициента Стьюдента». Для вероятности 95,0% и ( 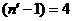; поправочный коэффициент t=2,776.

4. Получаем 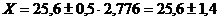. Значение 27,5 не входит в эти пределы. Его можно отбросить.

5. Значение измеряемой величины при надёжности 95%