Исследование функции по общей схеме.
1. Область определения функции f(x) – полностью может быть указана после исследования функции на непрерывность.
2. Непрерывность и точки разрыва функции f(x) исследуются по схеме:
> iscont(f, x=-infinity..infinity);
> d1:=discont(f,x);
> d2:=singular(f,x);
В результате наборам переменным d1и d2 будут присвоены значения x-координат в точках разрыва 1 и 2-го родов (если они будут найдены).
3. Асимптоты. Точки бесконечных разрывов определяют вертикальные асимптоты графика f(x). Уравнение вертикальной асимптоты имеет вид:
> yr:=d2;
Поведение функции f(x) на бесконечности характеризуется наклонными асимптотами (если они есть). Уравнение наклонной асимптоты y=kx+b, где коэффициенты вычисляются по формулам:
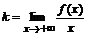и 
.
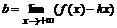Аналогичные формулы для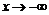 
. Поэтому нахождение наклонных асимптот можно провести по следующей схеме:
> k1:=limit(f(x)/x, x=+infinity);
> b1:=limit(f(x)-k1*x, x=+infinity);
> k2:=limit(f(x)/x, x=-infinity);
> b2:=limit(f(x)-k2*x, x=-infinity);
Часто оказывается, что k1=k2 и b1=b2, в этом случае будет одна асимптота 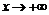при 
и при 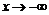. С учетом этого составляется уравнение асимптоты
> yn:=k1*x+b1;
4. Экстремумы. Исследование функции f(x) на экстремумы можно проводить по схеме:
> extrema(f(x), {}, x, ’s’);
> s;
> fmax:=maximize(f(x), x);
> fmin:=minimize(f(x), x);
После выполнения этих команд будут найдены координаты (x, y) всех максимумов и минимумов функции f(x).
Построение графика.
Построение графика функции f(x)– это окончательный этап исследования функции. На рисунке помимо графика исследуемой функции f(x) должны быть нанесены все ее асимптоты пунктирными линиями, подписаны координаты точек max и min. Приемы построения графиков нескольких функций и нанесения надписей были рассмотрены в теме III.
Задание 3.3.
1. Провести полное исследование функции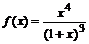 
по общей схеме. Сначала перейдите в текстовый режим и наберите “Исследование функции: “. Затем вернитесь в режим командной строки и наберите команды:
> f:=x^4/(1+x)^3:
В текстовом режиме наберите “Непрерывность функции”. В режиме командной строки и наберите:
> readlib(iscont): readlib(discont):
readlib(singular):
> iscont(f, x=-infinity..infinity);
false
Это означает, что функция не является непрерывной. Перейдите в текстовый режим и наберите “Нахождение точек разрыва”. Вернитесь в режим командной строки и наберите:
> discont(f,x);
{-1}
Конвертировать полученное значение точки разрыва типа set в число можно командой convert, добавив вторую опцию, например, `+`. Обратите внимание на обратные кавычки, которые набираются клавишей, расположенной выше клавиши табуляции.
> xr:=convert(%,`+`);
xr:= -1
Перейдите в текстовый режим и наберите: “Получена точка бесконечного разрыва x=-1”. С новой строки наберите: “Нахождение асимптот.”. Перейдите на новую строку и наберите “Уравнение вертикальной асимптоты: x=-1” (это можно сделать, поскольку вертикальные асимптоты возникают в точках бесконечного разрыва). С новой строки наберите: “Коэффициенты наклонной асимптоты:”. Перейдите в режим командной строки и наберите:
> k1:=limit(f/x, x=+infinity);
k1 :=1
> b1:=limit(f-k1*x, x=+infinity);
b1 := -3
> k2:=limit(f/x, x=-infinity);
k2 :=1
> b2:=limit(f-k2*x, x=-infinity);
b2 := -3
В этом случае коэффициенты наклонных асимптот пр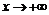и 
и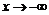 
оказались одинаковыми. Поэтому перейдите в текстовый режим и наберите “Уравнение наклонной асимптоты:”. Затем в новой строке прейдите в режим командной строки и наберите:
> y=k1*x+b1;
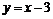
В текстовом режиме наберите “Нахождение экстремумов”. В новой строке наберите команды:
> readlib(extrema): readlib(maximize):
readlib(minimize):
> extrema(f,{},x,'s');s;
{ 
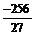, 0}
{{x= -4},{x=0}}
Поскольку функция имеет разрыв, то при поиске максимума и минимума следует указать интервал, в который не должна входить точка разрыва.
> fmax:=maximize(f,{x},{x=-infinity..-2});
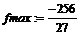
> fmin:=minimize(f,{x},{x=-1/2..infinity});
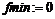
В текстовом режиме наберите результат исследования в виде:
“Максимум в точке (-4, -256/27); минимум в точке (0, 0).”
2. Построить график функции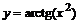 
и ее асимптоту, указать координаты точек экстремума. Оформление каждого этапа исследования функции проделать также как и при выполнении предыдущего задания. Самостоятельно загрузите из стандартной библиотеки все необходимые команды.
> restart: y:=arctan(x^2):
> iscont(y, x=-infinity..infinity);
true
> k1:=limit(y/x, x=-infinity);
k1:=0
> k2:=limit(y/x, x=+infinity);
k2:=0
> b1:=limit(y-k1*x, x=-infinity);
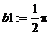
> b2:=limit(y-k1*x, x=+infinity);
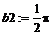
> yh:=b1;
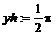
> extrema(y,{},x,'s');s;
{0}
{{x=0}}
> ymax:=maximize(y,{x}); ymin:=minimize(y,{x});
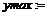
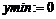
> with(plots): yy:=convert(y,string):
> p1:=plot(y,x=-5..5, linestyle=1, thickness=3,
color=BLACK):
> p2:=plot(yh,x=-5..5, linestyle=1,thickness=1):
> t1:=textplot([0.2,1.7,"Асимптота:"],
font=[TIMES, BOLD, 10], align=RIGHT):
> t2:=textplot([3.1,1.7,"y=Pi/2"],
font=[TIMES, ITALIC, 10], align=RIGHT):
> t3:=textplot([0.1,-0.2,"min:(0,0)"],
align=RIGHT):
> t4:=textplot([2,1,yy], font=[TIMES, ITALIC,
10], align=RIGHT):
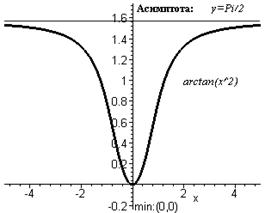
> display([p1,p2,t1,t2,t3,t4]);
§4. Интегрирование