Исследование системы регулирования с корректирующими звеньями

Цель работы

1. Построение моделей систем регулирования с последовательной и последовательно-параллельной коррекцией.

2. Определение переходных характеристик систем подчинённого регулирования.

3. Изучение влияния нелинейностей на динамические характеристики систем регулирования.

Теоретическое обоснование

Упрощённая структурная схема системы с последовательно-параллельной коррекцией представлена на рис. 9.1.

В этой системе регулятор компенсирует большую постоянную времени объекта и корректирует коэффициент усиления системы, определяемый постоянной интегрирования Т_и

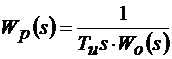. (9.1)

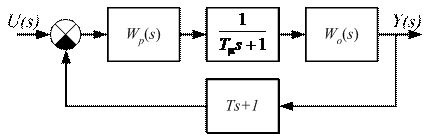
Рис. 9.1. Структурная схема системы с последовательно-параллельной коррекцией

В системах с последовательной коррекцией выполняется соотношение Т_и = аТ_μ, где а – коэффициент пропорциональности (настройки). При настройке системы на технический оптимум часто принимают а = 2.

Передаточная функция замкнутой системы с последовательно-параллельной коррекцией

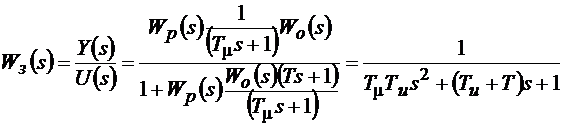. (9.2)

Собственная частота колебаний 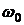и коэффициент демпфирования:

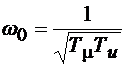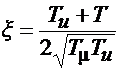; . (9.3)

При настройке системы подчинённого регулирования на технический оптимум коэффициент демпфирования равен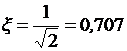

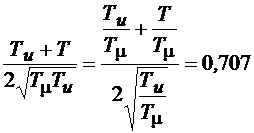. (9.4)

Равенство может выполняться при Т = 0 и тогда Т_и = 2Т_μ, что свидетельствует об отсутствии параллельной коррекции и настройке системы подчинённого регулирования на технический оптимум. Если же 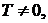то система настраивается на технический оптимум с использованием параллельной коррекции при коэффициенте настройки 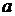меньшем, чем 2. Такая настройка применяется тогда, когда требуется повысить быстродействие системы, что часто имеет место при больших значениях Т_μ (Т_μ > 0). Отношение Т/Т_μ (Т_μ = 0 ¸ 0,5) позволяет вычислить отношения Т_и/Т_μ, которое определяет коэффициент демпфирования. При Т/Т_μ = 0 отношение Т_и/Т_μ = 2, что указывает на отсутствие параллельного корректирующего устройства. При Т/Т_μ ³ 0,5 равенство (9.4) выполняется при коэффициенте демпфирования больше оптимального (x > 0,707).

Вторым важным свойством последовательно-параллельной коррекции является малая чувствительность системы регулирования к изменениям параметров, например коэффициента усиления. Если 0,3 < Т/Т_μ £ 0,5 и по выражению (9.4) построить график x = f(Т_и/Т_μ), то получим, что изменение Т_и/Т_μ от 0,4 до 2,8 мало влияет на изменение коэффициента демпфирования.

Описание работы

На рис. 9.2А представлена структурная схема системы с последователь-ной коррекцией: 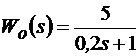; Т_μ = 0,04; Т/Т_μ = 0,35; x = 1,5.

Параметры регулятора определены соотношением

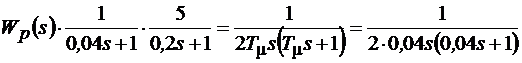. (9.5)

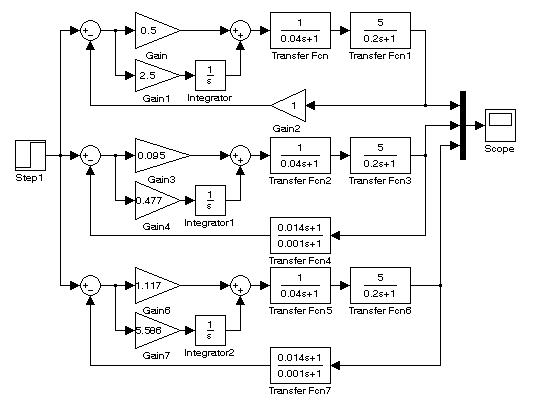
Рис. 9.2. Структурные схемы систем с последовательной (рис. 9.2А)

и последовательно-параллельной коррекцией (рис. 9.2Б, В)

Из (9.5) получаем передаточную функцию регулятора

.

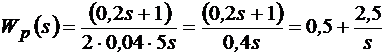Принимаем Т = 0,35 × 0,04 = 0,014.

Передаточная функция реального дифференцирующего звена имеет вид

.

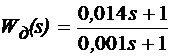Используя выражение (9.4) для принятого отношения Т/Т_μ = 0,35 определяем коэффициент настройки Т_и/Т_μ = а.

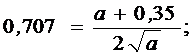а² – 1,3а + 0,1225 = 0; а₁ = 1,1977; а₂ = 0,1023. (9.6)

На рис. 9.2Б и рис. 9.2В представлены структурные схемы системы для а₁ = 1,1977 и а₂ =0,1023.

При этом Т_и1 = 0,35×1,1977 = 0,4192, Т_и2 = 0,35×0,1023 = 0,0358. Исходя из (9.1) , .

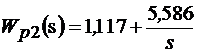Для построения графиков переходных характеристик можно исполь-зовать отдельные подсистемы схемы рис. 9.2 (рис. 9.3 и рис. 9.4).

А)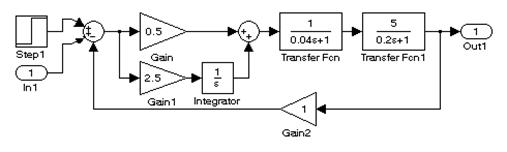

Б)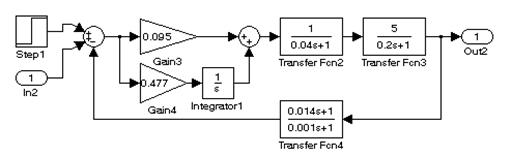

В)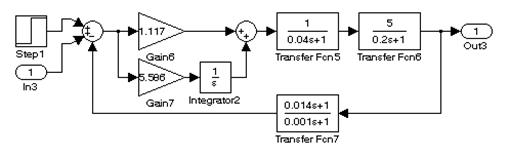

Рис. 9.3. Построение графиков переходных характеристик

[A,B,C,D]=linmod('mod09_2');w=ss(A,B,C,D),w1=tf(w)

[A,B,C,D]=linmod('mod09_3');w=ss(A,B,C,D),w2=tf(w)

[A,B,C,D]=linmod('mod09_4');w=ss(A,B,C,D),w3=tf(w)

figure(1),step(w1,w2,w3),grid %Переходные характеристики.

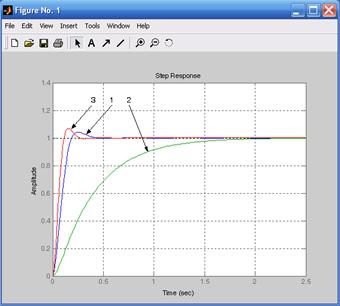
1 – а = 2; 2 – а = 1,1977; 3 – а = 0,1023

Рис.9.4. Результат моделирования структурных схем, представленных на рис. 9.3

Коэффициент настройки, равный двум, соответствует системе с последовательной коррекцией, коэффициенты 1,1977 и 0,1023 – системам с последовательно-параллельной коррекцией.

На рис. 9.5А и рис. 9.5B представлены схемы с последовательной и последовательно–параллельной коррекцией. На рис. 9.5C и рис. 9.5D представлены те же системы, но с увеличенной в 2 раза постоянной времени объекта. В системе с последовательно–параллельной коррекцией изменение параметров системы (постоянной времени) меньше влияет на качественные показатели переходных характеристик.

А)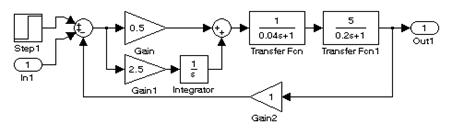

B)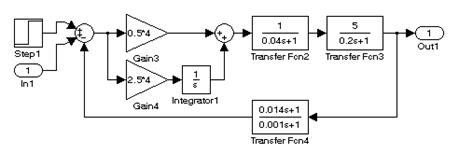

C)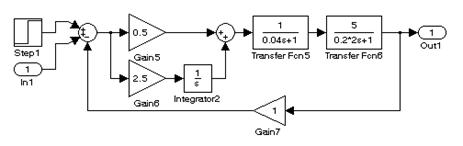

D)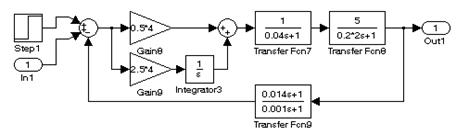

Рис. 9.5. Исследование чувствительности систем к изменению постоянных

времени объекта при различных видах обратной связи

[A,B,C,D]=linmod('mod09_2');w=ss(A,B,C,D);w1=tf(w)

[A,B,C,D]=linmod('mod09_6');w=ss(A,B,C,D);w2=tf(w)

[A,B,C,D]=linmod('mod09_7');w=ss(A,B,C,D);w3=tf(w)

[A,B,C,D]=linmod('mod09_8');w=ss(A,B,C,D);w4=tf(w)

figure(2); step(w1,w2,w3,w4),grid %Переходные характеристики.

На рис. 9.6 представлены структурные схемы, позволяющие сравнить чувствительность систем с различными видами обратных связей при изменении коэффициента усиления разомкнутой системы.

А)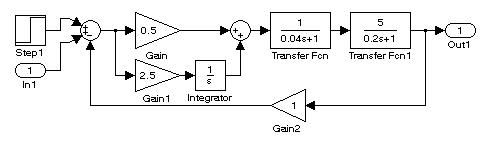

B)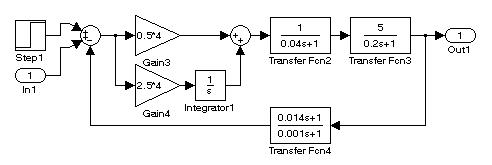

C)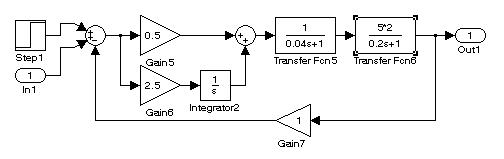

D)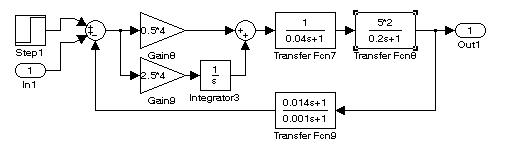

Рис. 9.6. Исследование чувствительности систем к изменению постоянных времени объекта

[A,B,C,D]=linmod('mod09_2');w=ss(A,B,C,D);w1=tf(w)

[A,B,C,D]=linmod('mod09_6');w=ss(A,B,C,D);w2=tf(w)

[A,B,C,D]=linmod('mod09_10');w=ss(A,B,C,D);w3=tf(w)

[A,B,C,D]=linmod('mod09_11');w=ss(A,B,C,D);w4=tf(w)

figure(3);step(w1,w2,w3,w4),grid %Переходные характеристики.

На рис. 9.7 изображены графики переходных характеристик с увеличенной в два раза постоянной времени объекта, на рис. 9.8 изображены графики переходных характеристик с увеличенным в два раза коэффициентом усиления объекта.

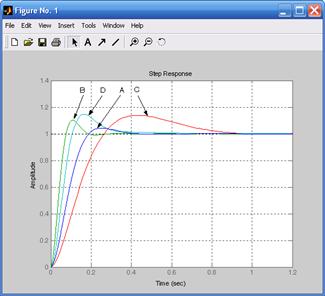
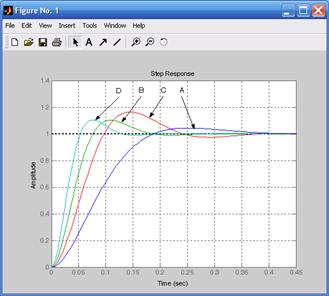
Рис. 9.7. Переходные процессы, Рис. 9.8. Переходные процессы,

соответствующие структурным соответствующие структурным

схемам рис. 9.5 схемам рис. 9.6

Из кривых, представленных на рис. 9.8 следует, что отклонение коэффи-циента усиления от оптимального ухудшает качество переходных процессов. Однако в системах, использующих последовательно-параллельную коррек-цию, ухудшение переходных характеристик выражено слабее.

Задание

1. Для заданного отношения постоянной времени дифференцирования 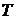и малой некомпенсируемой постоянной времени Т_μ 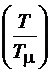, коэффициента демпфирования 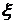определить параметры реального дифференцирующего звена и коэффициенты настройки .

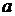2. Определить для рассчитанного коэффициента настройки параметры регулятора.

3. Построить структурные схемы регулирования с последовательной и последовательно- параллельной коррекцией.

4. Определить влияние коэффициента настройки, параметров регулятора и параметров объекта на переходные характеристики системы.

Содержание отчета

1. Методика определения параметров регулятора с последовательной коррекцией.

2. Методика определения параметров регулятора с последовательно–параллельной коррекцией.

3. Определение для заданного варианта параметров регулятора с последовательной коррекцией.

4. Определение для заданного варианта параметров регулятора с последовательно–параллельной коррекцией.

5. Структурные схемы систем в соответствии с рис. 9.2, 9.4, 9.6.

6. Графики результатов моделирования структурных схем в соответствии с 9.3, 9.5, 9.7.

7. Общие выводы о проделанной работе.

Контрольные вопросы

1. Обоснуйте методику определения параметров регуляторов при последовательной коррекции.

2. Обоснуйте методику определения параметров регуляторов при последовательно–параллельной коррекции.

3. Дайте сравнительную характеристику систем с последовательной и последовательно–параллельной коррекцией. Обоснуйте область применения систем с последовательно–параллельной коррекцией.

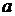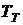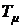4. Определите коэффициент пропорциональности (коэффициент настройки - ) между и в системах с последовательно–параллельной коррекцией, если известны, что 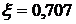, а .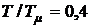

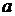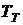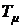5. Определите коэффициент пропорциональности (коэффициент настройки - ) между и в системах с последовательно–параллельной коррекцией, если известны, что 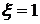, а .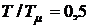

Лабораторная работа № 10