Построение трехмерных графиков.

1 Введите вектора x1 и x2 (например, последовательности от 1 до 10).

2 Создайте из них матрицу: [x1, x2]= meshgrid(x1,x2).

3 Задайте функцию z=x1.*sin(x1+x2) (примечание: функция может быть задана не формулой, а матрицей значений z).

4 Постройте график: meshc(x1,x2,z).

5 Сохраните график для возможности вставки в документ, для этого выберите меню File–>export. Выберите тип файла, который можно вставить в документ и дайте имя файлу.

Порядок выполнения работы.

1 Введите матрицы х1 и х2.

2 Вычислите коэффициенты регрессии по методу наименьших квадратов.

3 Постройте графики по исходным данным и по полученному уравнению регрессии. Сравните результаты.

4 Вычислите значение коэффициента множественной корреляции.

5 Постройте уравнения частной регрессии у по х1 и по х2.

6 Сделайте вывод об адекватности линейной модели.

Содержание отчета

Отчет должен содержать:

– вид полученной функции множественной линейной регрессии, метод получения значений ее коэффициентов (последовательность команд);

– последовательность команд для получения значения коэффициента множественной корреляции и его значение;

– уравнения частной регрессии;

– выводы на основе анализа значения коэффициента множественной корреляции.

ЛАБОРАТОРНАЯ РАБОТА № 5

Тема: ФАКТОРНЫЙ АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Цель работы. Ознакомление с методом факторного анализа.

Краткие сведения из теории

Факторный анализ – это статистический метод анализа результатов наблюдений, зависящих от различных, одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния.

Идея факторного анализа заключается в разложении общей дисперсии случайной величины на независимые случайные слагаемые, каждое из которых характеризует влияние того или иного фактора.

Пусть Х – случайная величина, А и В – влияющие на нее факторы, 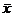– среднее значение величины Х. Допустим, что отклонение Х от 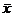при действии факторов А и В можно представить в виде суммы

,

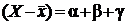где a – отклонение, вызываемое фактором А;

b – отклонение, вызываемое фактором В;

g – отклонение, вызываемое другими неучтенными факторами.

Обозначим дисперсии Х, a, b, g соответственно .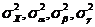

Тогда имеет место равенство:

.

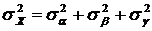Сравнивая значения дисперсий, можно установить степень влияния факторов на величину Х.

Пусть имеется r значений фактора А и s значений фактора В; x_ij – значение величины Х при i–м значении фактора А и j–м значении фактора В. Тогда наблюдаемые значения величины Х можно представить в виде матрицы, строки которой соответствуют уровням фактора А, а столбцы – уровням фактора В. Вычислим средние значения по каждому столбцу, строке, а также общее среднее:

, , .

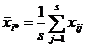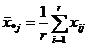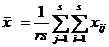Тогда основное тождество факторного анализа имеет вид:

.

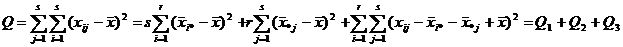Слагаемое Q₁ характеризует изменение признака по фактору А, Q₂ –по фактору В, Q₃ – влияние неучтенных факторов.

Произведем оценку дисперсий:

;

;

;

.

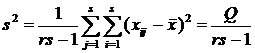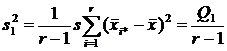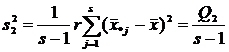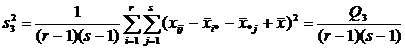Известно, что если случайная величина распределена нормально, то отношение выборочных дисперсий имеет F - распределение.

, .

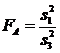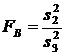Полученные значения F_A и F_B сравнивают с табличными при выбранном уровне значимости. Если значения меньше табличных, влияние факторов считается незначительным.

Задание к лабораторной работе

В матрице даны значения величины y при различных значениях факторов х1 (изменяется по строкам) и х2 (изменяется по столбцам). Выполнить факторный анализ: определить существенность влияния каждого из факторов на величину y при уровне значимости 0.01.

Порядок выполнения работы

1 Введите заданную матрицу (ее можно скопировать) и вставить в MATLAB, оформив в соответствующем формате.

2 Вычислите среднее арифметическое элементов матрицы.

3 Вычислите средние по столбцам.

Вычисление суммы элементов столбцов матрицы a:

>>sum(a)

Результатом является вектор, элементы которого являются суммами элементов по каждому столбцу матрицы. Для вычисления среднего арифметического разделите этот вектор на количество элементов в столбце.

4 Вычислите средние по строкам.

Для вычисления суммы элементов строки матрицы а можно воспользоваться той же функцией, предварительно выполнив транспонирование матрицы:

>>sum(a’)

(при транспонировании строки превращаются в столбцы, а столбцы – в строки, операция транспонирования – «’»).

5 Из полученных средних по строкам и по столбцам сформируйте матрицы таким образом, чтобы из элементов каждой строки исходной матрицы можно было вычесть ее среднее значение (по строке), а из элементов каждого столбца – его среднее (то есть нужно получить 2 матрицы 10х10, в одной из которых все элементы строки равны среднему по этой строке, а во второй – все элементы столбца равны среднему по этому столбцу).

Прежде чем переходить к операциям с большими матрицами, выполните следующие действия с матрицами 2х2.

а) Вычесть из 1-й строки матрицы а размером 2х2 единицу, из 2-й строки – двойку.

Решение. Для этого необходимо сформировать матрицу такого же размера, в каждой строке которой содержатся единицы, а во второй – двойки.

Пример. Пусть матрица а задана следующим образом:

>>a=[1 2; 3 4]

Зададим матрицу b:

>>b=[1 1; 2 2]

>> a=a–b

б) Вычесть из 1-го столбца матрицы а размером 2х2 единицу, из 2-го столбца – двойку.

Решение. Для этого необходимо сформировать матрицу такого же размера, содержащую в каждом столбце число, которое необходимо вычесть.

Пример. Для той же матрицы а сформируем новую матрицу b:

>>b=[1 2; 1 2]

в) Операции объединения матриц.

Можно получить матрицу, являющуюся объединением других матриц. Матрицы при этом задаются так же , как элементы матриц.

Пример. Пусть вектор b=[1 2].

Тогда операция

>> b=[b b]

даст вектор b=[ 1 2 1 2],

а операция

>>b=[b;b]

даст матрицу b=[1 2; 1 2].

Операция

>> b=[b’ b’]

в результате даст матрицу b=[1 1; 2 2]

6 Вычислите значения s1², s2², s3².

7 Вычислите значения F–распределения для обоих факторов.

8 Имея в виду, что табличное значение F–распределения равно 5.35, сделайте вывод о необходимости учета влияния каждого фактора.

Варианты заданий

Вариант 1

29.90 32.29 36.07 41.19 47.62 55.32 64.26 74.44 85.83 98.42

29.95 32.34 36.12 41.24 47.67 55.37 64.31 74.49 85.88 98.47

30.02 32.40 36.19 41.31 47.74 55.44 64.38 74.56 85.95 98.54

30.10 32.49 36.27 41.40 47.82 55.52 64.47 74.64 86.03 98.63

30.20 32.58 36.37 41.49 47.92 55.62 64.56 74.74 86.13 98.72

30.31 32.69 36.48 41.60 48.03 55.73 64.67 74.85 86.24 98.83

30.43 32.81 36.60 41.72 48.15 55.85 64.79 74.97 86.36 98.95

30.56 32.95 36.73 41.85 48.28 55.98 64.93 75.10 86.49 99.08

30.70 33.09 36.87 42.00 48.42 56.12 65.07 75.24 86.64 99.23

30.85 33.24 37.02 42.15 48.57 56.27 65.22 75.40 86.79 99.38

Вариант 2

21.26 21.58 21.88 22.16 22.44 22.72 22.99 23.26 23.52 23.78

23.96 24.27 24.57 24.86 25.14 25.42 25.69 25.96 26.22 26.48

28.45 28.77 29.07 29.36 29.64 29.91 30.18 30.45 30.71 30.98

34.75 35.06 35.36 35.65 35.93 36.21 36.48 36.74 37.01 37.27

42.84 43.15 43.45 43.74 44.02 44.30 44.57 44.83 45.10 45.36

52.73 53.04 53.34 53.63 53.91 54.18 54.46 54.72 54.99 55.25

64.41 64.73 65.03 65.31 65.60 65.87 66.14 66.41 66.67 66.93

77.90 78.21 78.51 78.80 79.08 79.36 79.63 79.89 80.16 80.42

93.18 93.50 93.79 94.08 94.36 94.64 94.91 95.18 95.44 95.70

110.26 110.58 110.88 111.16 111.44 111.72 111.99 112.26 112.52 112.78

Вариант 3

3.43 9.86 20.06 33.87 51.19 71.94 96.06 123.49 154.19 188.13

3.59 10.02 20.22 34.03 51.35 72.10 96.22 123.65 154.35 188.29

3.69 10.13 20.33 34.14 51.46 72.21 96.32 123.75 154.45 188.39

3.77 10.21 20.41 34.22 51.54 72.28 96.40 123.83 154.53 188.47

3.84 10.27 20.47 34.28 51.60 72.35 96.47 123.90 154.60 188.53

3.89 10.33 20.53 34.34 51.66 72.40 96.52 123.95 154.65 188.59

3.94 10.37 20.57 34.39 51.70 72.45 96.57 124.00 154.70 188.64

3.98 10.42 20.62 34.43 51.75 72.50 96.61 124.04 154.74 188.68

4.02 10.46 20.66 34.47 51.79 72.53 96.65 124.08 154.78 188.72

4.06 10.49 20.69 34.50 51.82 72.57 96.69 124.12 154.82 188.75

Вариант 4

23.71 24.72 25.98 27.41 29.00 30.72 32.56 34.50 36.55 38.69

23.96 24.98 26.23 27.66 29.25 30.97 32.81 34.76 36.80 38.95

24.38 25.40 26.65 28.09 29.67 31.39 33.23 35.18 37.23 39.37

24.97 25.99 27.24 28.68 30.26 31.98 33.82 35.77 37.82 39.96

25.73 26.75 28.00 29.44 31.02 32.74 34.58 36.53 38.58 40.72

26.66 27.68 28.93 30.37 31.95 33.67 35.51 37.46 39.51 41.65

27.76 28.77 30.03 31.46 33.05 34.77 36.61 38.56 40.60 42.74

29.02 30.04 31.29 32.73 34.32 36.03 37.87 39.82 41.87 44.01

30.46 31.48 32.73 34.16 35.75 37.47 39.31 41.26 43.30 45.44

32.06 33.08 34.33 35.77 37.35 39.07 40.91 42.86 44.91 47.05

Вариант 5

27.08 28.94 31.34 34.18 37.40 40.97 44.84 49.01 53.44 58.12

27.17 29.02 31.42 34.27 37.49 41.05 44.93 49.09 53.53 58.21

27.27 29.12 31.52 34.36 37.59 41.15 45.03 49.19 53.62 58.31

27.37 29.23 31.63 34.47 37.69 41.26 45.13 49.30 53.73 58.41

27.48 29.34 31.74 34.58 37.80 41.37 45.24 49.41 53.84 58.52

27.60 29.45 31.85 34.69 37.92 41.48 45.36 49.52 53.95 58.64

27.71 29.57 31.97 34.81 38.03 41.60 45.48 49.64 54.07 58.76

27.84 29.69 32.09 34.93 38.16 41.72 45.60 49.76 54.19 58.88

27.96 29.82 32.22 35.06 38.28 41.85 45.72 49.89 54.32 59.00

28.09 29.94 32.34 35.19 38.41 41.97 45.85 50.01 54.45 59.13

Вариант 6

11.42 11.64 11.90 12.18 12.49 12.82 13.16 13.52 13.89 14.27

12.93 13.15 13.40 13.69 14.00 14.32 14.66 15.02 15.39 15.78

16.46 16.68 16.94 17.22 17.53 17.86 18.20 18.56 18.93 19.31

22.70 22.92 23.18 23.46 23.77 24.10 24.44 24.80 25.17 25.55

32.25 32.47 32.73 33.01 33.32 33.65 33.99 34.35 34.72 35.10

45.67 45.89 46.15 46.43 46.74 47.07 47.41 47.77 48.14 48.52

63.49 63.71 63.97 64.25 64.56 64.89 65.23 65.59 65.96 66.34

86.21 86.43 86.69 86.98 87.28 87.61 87.95 88.31 88.68 89.06

114.32 114.54 114.80 115.08 115.39 115.71 116.05 116.41 116.78 117.17

148.27 148.49 148.74 149.03 149.34 149.66 150.00 150.36 150.73 151.12

Содержание отчета

– понятие и назначение факторного анализа, основная идея и вычисление дисперсий;

– листинг сессии вычисления дисперсий;

– выводы о значимости факторов.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Максимей, И.В. Имитационное моделирование на ЭВМ / И.В. Максимей. – М : «Радио и связь», 1988. – 227 с.

2. Петрович, М.Л. Регрессионный анализ и его математическое обеспечение на ЕС ЭВМ / М.Л. Петрович. – М : «Финансы и статистика», 1982. – 194 с.

3. Бусленко, Н.П. Моделирование сложных систем / Н.П. Бусленко.– М: «Наука», 1968. – 355 с.

4. Адаптивные системы автоматического управления: учеб. пособие / под ред. В.Б. Яковлева. – Л. : Изд-во Ленинградского университета, 1984. – 202 с.

5. Хорафас, Д.Н. Системы и моделирование / Д.Н. Хорафас. – М : «Мир», 1967. – 410 с.

6. Перегудов, Ф.И. Введение в системный анализ / Ф.И. Перегудов, Ф.И. Тарасенко. – М : «Высш. школа», 1989. – 367 с.

7. Системный анализ и структуры управления / под ред. В.Г. Шорина. – М : «Знание», 1975. – 303 с.

8. Бусленко, Н.П. Лекции по теории сложных систем / Н.П. Бусленко, В.В. Калашников, И.Н. Коваленко. – М : «Сов. радио», 1973. – 439с.

9. Ермаков, С.М. Статистическое моделирование / С.М. Ермаков, Г.А. Михайлов. – М : «Наука», 1982. – 296 с.

10. Новгородцев, А. Расчет электрических цепей в MATLAB / А. Новгородцев. – СПб : «ПИТЕР», 2004. – 250 с.

11. Дьяконов, В.П. MATLAB 6.5 в математике и моделировании / В.П. Дьяконов. – М : «СОЛОН–Пресс», 2003. – 560 с.