Об использовании операторов break continue return

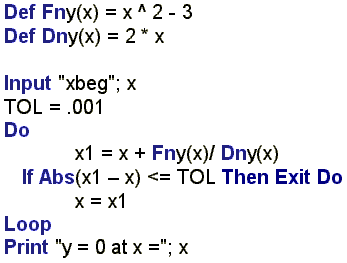Попробуем на простых примерах показать, что ввод в язык Mathcad операторов break, continue и return (см. выше) – только полшага в сторону повышения гибкости управляющих конструкций этого языка программирования.

Рис. 4.5 - Метод Ньютона I (BASIC): цикл с выходом из середины

На рис. 4.5 приведена BASIC-программа поиска корня алгебраического уравнения методом Ньютона (касательных). Почему мы начали с языка BASIC, ведь этюд посвящен языку программирования Mathcad? Дело в том, что язык BASIC кроме традиционной тройки циклов (цикл с предпроверкой, цикл с постпроверкой, цикл с параметром) имеет и универсальный цикл с выходом из середины: Do [...] If ... Then [...] Exit Do [...] Loop. Эта конструкция наряду с другими преимуществами, о которых будет сказано ниже, позволяет реализовывать алгоритмы в их естественной последовательности. Так, в программе на рис. 6.8 объявляются функции пользователя (анализируемое уравнение y и его производная dy), запрашивается значение начального приближения к корню x и задается значение погрешности TOL. После этого организуется цикл, но не традиционный, а с выходом из середины. В цикле, следуя естественному порядку алгоритма Ньютона, рассчитывается новое приближение к корню (x1), и если оно отстает от предыдущего не более чем на величину заданной погрешности, то (Then) задача считается решенной (Exit Do). Если нет, то ведется подготовка к новому приближению (x = x1), а цикл повторяется (Loop).

При реализации на языке Mathcad этот несложный алгоритм обрастает «архитектурными излишествами», так как его приходится реализовывать функцией и «запихивать» в прокрустово ложе цикла while – см. рис. 4.6.

Рис. 4.6 - Метод Ньютона II: цикл с предпроверкой

Цикл с предпроверкой (цикл while) требует, чтобы булево выражение заголовка было определено еще до входа в цикл. А этого нет при поиске корня методом Ньютона. Приходится до входа (и для входа) в цикл писать x1 ←x + 2 × TOL. Подобным образом лгут детям (а машина тоже в каком-то смысле дитя), заставляя их что-то делать. Строку x1 ←x + 2 × TOL можно уподобить стартеру двигателя внутреннего сгорания, работающего, кстати, как и программа на рис. 4.6, циклически. Вот какими аллегориями (дитя, двигатель) обросла наша простенькая программа из-за того, что в языке Mathcad нет цикла с выходом из середины. На рис. 4.6 можно отметить и другую ненатуральность программы – постановку телеги впереди лошади: в цикле сначала приходится готовиться к новому приближению (x1 ←x), хотя еще не ясно, понадобится оно или нет, а только потом проводить его.

Операторы break, continue и return, введенные в Mathcad, призваны вернуть программе на рис. 4.6 ее естественность, но...

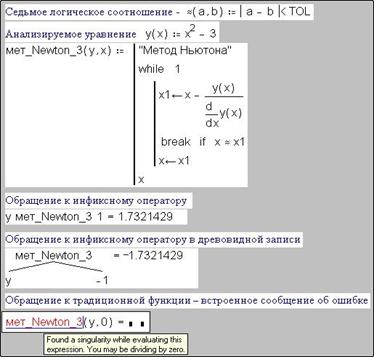Рис. 4.7 - Метод Ньютона III: имитация цикла с выходом из середины

Оператор continue отличается от оператора break тем, что передает управление не в хвост, а в гриву (начало) цикла.

Остается рассказать о последней кнопке на панели программирования Mathcad 8 Pro. Нажатие на нее приводит к появлению на дисплее заготовки инфиксного оператора обработки ошибок с двумя операндами:

Суть оператора проста: если при выполнении правого операнда возникнет ошибка, то выполняется левый операнд. Этот оператор позволяет реализовывать в Mathcad-программах метод проб и ошибок.

Испробуем on error, на простом примере:

Но оказалось, что объявленная таким образом функция y(х) возвращает нуль, а не единицу при x = 0. Дело в том, что система Mathcad, оптимизируя произведение, выдает нуль, если первый сомножитель равен нулю. Функцию y(х) нужно переписать по другому:

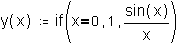но и эта запись не совсем правомочна. Проще записать:

Здесь графически решается неравенство: функция f(x) возвращает нуль не только тогда, когда логарифм меньше единицы, но и тогда, когда делается попытка взятия логарифма от неположительного числа. Можно, конечно, решить квадратное уравнение и обойти ошибку функцией или оператором if.

Контрольные вопросы:

1. Знать основные компоненты Математического пакета Mathcad

2. Дать описание всем инструментам, находящимся на панели «Программирование», уметь их практически использовать.

Задание:

1. Задание на закрепление пройденного: сделать программу на рис. 4.3 рекуррентной, а на рис. 4.4 – рекурсивной.

2. Задания 1 выполнить в среде математического пакета Mathcad.

ЛАБОРАТОРНАЯ РАБОТА №5

Тема: Программа сканирования и распознования текстов FineReader.

Цель работы: Ознакомление с принципом работы програм сканирования текста, а также приобретение навыков работы с программой FineReader.

Введение

Все мы вводим тексты в компьютер. Это могут быть газетные вырезки, журнальные статьи, прошлогодние договоры, деловые письма, факсы, прайс - листы, биржевые сводки, анкеты... Подсчитано, что более 90% современных документов поступает к нам на бумаге. Десятилетия люди знали только один способ ввода печатных документов в компьютер - с клавиатуры. Помните часы, которые Вы просиживали за компьютером, перепечатывая текст длиной в ве­чность? А как бы нам всем хотелось, чтобы компьютер научился читать сам прямо с бумажного листа!

Программа оптического рас­познавания текстов (по-английски OCR – Optical Character Recognition) FineReader позволит Вашему компьютеру и сканеру самостоятельно читать печатные тексты.