В общем случае мерой количества информации в сообщениях должна служить величина, измеряющая степень уменьшения неопределенности интересующего события под действием сообщения.
ВВЕДЕНИЕ
С вступлением современного общества в новый этап своего развития, получивший название информационного, информационные ресурсы играют не меньшую, а нередко и большую роль, чем ресурсы материальные. Знание о цене товара (например, кирпича), о возможности его доставки может существенно влиять на стоимость строительства. С позиций рынка информация давно стала товаром.
В настоящее время по данным ЮНЕСКО уже более половины всего занятого населения индустриально развитых стран принимают участие в информационных технологиях. В связи с этим возникла тенденция перекачивания трудовых резервов из сферы материального производства в информационную сферу. При этом в производственной сфере наблюдается широкое использование автоматизированных производств, базирующихся на информационных технологиях.
Целью пособия по дисциплине «Теория информационных процессов и систем» является изложение основных фундаментальных вопросов теории передачи и обработки информации, построения наиболее распространенных информационных систем различного назначения, необходимых для того, чтобы «…достичь заветной цели слияния технологий не только локальных и глобальных сетей, но и технологий любых информационных сетей – вычислительных, телефонных, телевизионных и т.п.» [1].
В пособии, в отличие от аналогичных изданий, рассмотрены промышленные информационно-измерительные, информационно-вычислительные, информационно-управляющие, информационно-платежные системы, применительно к которым излагаются вопросы сбора, передачи и обработки информации. На содержательную сторону пособия оказал заметное влияние источник [2], рекомендованный Министерством образования РФ в качестве учебника для студентов, обучающихся по направлению «Информационные системы». В данном пособии, в отличие от источника [2], сделана попытка устранения разрозненности некоторых разделов путем введения, в частности, сравнительной оценки реальных информационных каналов с идеальным каналом по Шеннону.
Материалы учебного пособия могут быть использованы студентами специальности 230201 – «Информационные системы и технологии» при изучении следующих специальных дисциплин: «Информационные сети», «Аппаратно-программные комплексы информационных систем», «Автоматизированные информационно-управляющие системы», «Информационно-измерительные системы». Данное пособие полезно и для бакалавров, и для магистрантов, обучающихся по направлению 230200 – «Информационные системы».
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Понятие информации
Для современных информационных систем ключевым является термин «информация». Не смотря на то, что с понятием информации мы широко сталкиваемся, строгого и общепринятого ее определения до сих пор не существует. Поэтому вместо определения обычно используют понятие об информации.
С учетом интуитивной точки зрения понятие «информация» может быть истолковано как некоторая совокупность сведений, определяющих меру наших знаний о тех или иных событиях, явлениях или фактах. Такое определение, характерное для естественных наук, может быть отвергнуто в социальных науках.
Более того, в современных информационных системах информация может обрабатываться без участия человека, и ни о каком знании или незнании здесь речь идти не может.
Введенные К. Шенноном количественные меры информации, не смотря на их объективность, не учитывают ценность или семантику информации. Поэтому эти меры невозможно использовать, к примеру, для сравнительной оценки научных открытий или произведений искусства.
Введем основные определения.
1. Информационный процесс – это любой процесс, в котором присутствует хотя бы один из элементов: передача информации, ее прием, хранение, обработка, выдача пользователю.
2. Информационная система – это любая система, реализующая или поддерживающая информационный процесс.
Система передачи информации
Объектом передачи в любой системе передачи информации является сообщение, несущее какую-либо информацию. Каждый из нас неоднократно употреблял выражение «масса информации», однако немногие знают, что можно измерять информацию количественно. Прежде чем вводить систему формул и чисел, рассмотрим пример. Пусть 10 июля мы услышали сообщение бюро прогнозов: «Осадков в виде снега завтра в Москве не будет». За последние 100 лет 10 июля в Москве снега, вероятно, ни разу не было, поэтому услышанное нами сообщение содержит в себе очень мало нового – мало информации. Если бы, однако, мы, зная, что работа бюро прогнозов надежна, услышали, что «завтра будут осадки в виде снега», то в этом сообщении для нас содержалось бы гораздо больше информации, чем в предыдущем. Таким образом, сообщение о том, что произойдет событие, которое должно произойти почти наверняка, содержит в себе очень мало информации. Напротив, сообщение о том, что произойдет событие, которое почти наверняка произойти не должно, содержит много информации. Сообщение о некотором событии содержит тем больше информации, чем больше изменяется вероятность этого события после приема сообщения о нем, по сравнению с вероятностью того же события до того, как было принято соответствующее сообщение.
Прямоугольных импульсов
Пусть модулирующий сигнал представляет периодическую последовательность прямоугольных импульсов (ПППИ) (рис. 2.4, а). В общем случае при амплитудной манипуляции с учетом выражений (2.2) и (2.3) модулируемый сигнал (рис. 2.4, б) будет иметь два значения: максимальное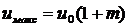 
и минимальное 
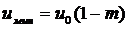. Амплитудная манипуляция используется в модемах при передаче цифровой информации.
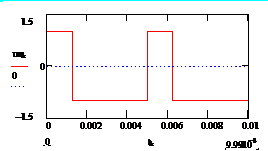
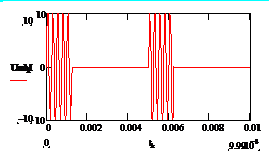
а б
Рис. 2.4. Амплитудная манипуляция: а – модулирующий сигнал,
б – амплитудно-манипулированное колебание
Часто при амплитудной манипуляции выбирают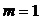 
. Тогда 
, 
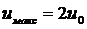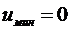, т.е. для сообщений закодированных, например двоичных кодов, при передаче символа 1 несущая излучаться будет, при передаче символа 0 излучение отсутствует.
ПППИ можно рассматривать как сложный сигнал, состоящий из отдельных гармонических составляющих. Эти составляющие для несмещенной ПППИ можно получить из разложения исходного сигнала в ряд Фурье [2]:
,
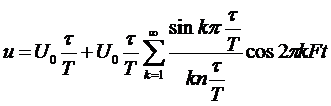где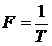 
– частота следования импульсов.
Как уже отмечалось, каждая составляющая с частотой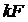 
, входящая в спектр прямоугольных импульсов, обусловит появление в спектре манипулированного сигнала двух боковых частот 
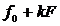и 
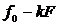. Спектр прямоугольных импульсов приведен на рис. 2.5, а, а спектр манипулированного сигнала – на рис. 2.5, б.
В общем случае, когда известен спектр модулированного сигнала, спектр АМ-колебания можно построить по следующему правилу: сместить спектр модулирующего сигнала на интервал частот, равный несущей частоте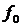 
, и зеркально отобразить относительно спектральной линии на несущей частоте.
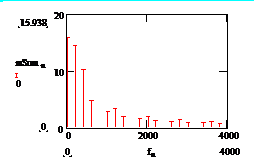
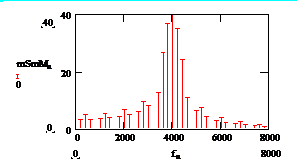
а б
Рис. 2.5. Спектр:
а – последовательности прямоугольных импульсов,
б – амплитудно-манипулированного сигнала
Гармоническим сигналом
Выбирая в формуле (2.1) с ЧМ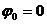 
, колебание при тональной частотной модуляции можно записать в следующем виде [2]:
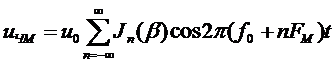, (2.7)
где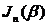 
– функция Бесселя первого рода порядка n;
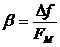– индекс частотной модуляции ( 
);
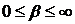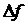– максимальное отклонение или девиация частоты при модуляции относительно частоты 
.
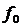Если принять отклонение фазы при ФМ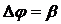 
, то выражение (2.7) будет справедливо для ФМ-колебаний с тональной модуляцией, что позволило [см. формулы (2.2)] объединить ЧМ и ФМ под одним названием: угловая модуляция. Учитывая это, в дальнейшем будем рассматривать только ЧМ.
На рис. 2.8 приведен спектр ЧМ-колебания. Этот спектр дискретен и состоит из колебаний с несущей частотой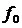 
, амплитуда которой пропорциональна функции Бесселя нулевого порядка 
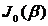и бесконечного числа симметричных боковых частот 
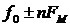с амплитудами, пропорциональными функциям Бесселя соответствующих порядков.
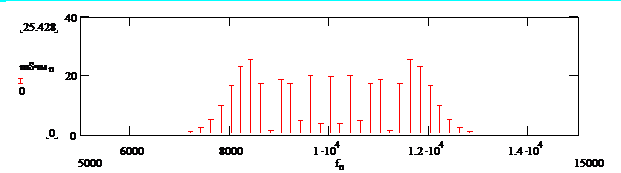Рис. 2.8. Спектр амплитуд частотно-модулированного сигнала
2.8. Частотная манипуляция последовательностью
прямоугольных импульсов
Сигнал после частотной манипуляции, используемой в модемах, должен иметь два граничных значения частоты: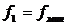 
и 
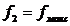. Напряжение, частота которого имеет два значения, показано на рис. 2.9. Такое напряжение можно представить как сумму сигналов 
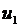и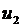 
с амплитудной манипуляцией ( 
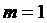), т.е. получающихся от двух генераторов с амплитудной манипуляцией.
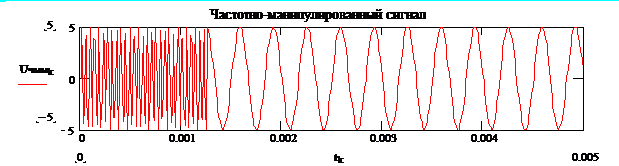
Рис. 2.9. Частотная манипуляция
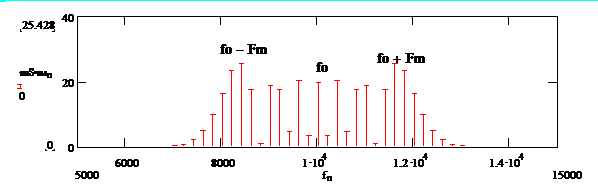Рис. 2.10. Спектр частотно-манипулированного сигнала
Если при частотной манипуляции модулирующим сигналом является последовательность прямоугольных двухполярных импульсов с периодом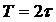 
, то выражение для частотно-манипулированного без разрыва фазы колебания будет иметь следующий вид:
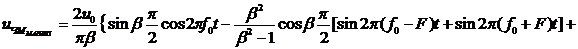
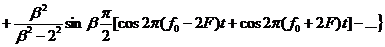, (2.8)
где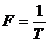 
– частота следования импульсов;
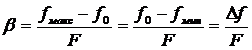– индекс ЧМ при частотной манипуляции.
Из выражения (2.8) следует, что при частотной манипуляции спектр сигнала состоит из колебаний на несущей частоте 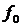и на боковых частотах 
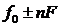, как и в случае гармонического модулирующего сигнала, но амплитуды колебаний другие. На рис. 2.10 приведен характерный спектр сигнала с частотной манипуляцией.
При частотной модуляции
Полоса частот, занимаемая ЧМ-колебанием, строго говоря, бесконечна. Реальные устройства и каналы связи имеют ограниченные полосы пропускания, что накладывает ограничение ширины спектра при ЧМ. На практике учитывают только те компоненты спектра, амплитуды которых превышают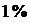 
от амплитуды немодулированной несущей, что позволяет ограничить полосу ЧМ-колебания на энергетической основе. На той же основе с достаточной точностью ширину полосы частот 
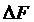при тональной модуляции можно вычислить с помощью формул, полученных Манаевым Е.И.:
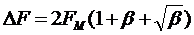, (2.9)
или
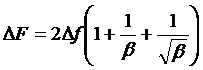. (2.10)
Из формулы (2.9) следует, что при небольших индексах модуляции (практически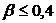 
) ширина полосы частот равна 
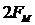, как в случае с АМ. Из формулы (2.10) следует, что при больших значениях 
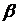ширина полосы частот 
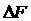стремится к значению 
.
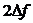Модель помехи
В информационных системах (ИС) наряду с полезным сигналом имеют место различного рода помехи. Достаточно распространенными являются помехи в виде случайных процессов с нормальным законом распределения. К таким помехам относятся так называемые внутренние шумы ИС, обусловленные дискретной природой электрического тока, представляющего перемещение элементарных зарядов (к примеру, электронов) в электрических цепях и приборах. Термин «шумы» применительно к помехам впервые появился в телефонии и в дальнейшем стал общепринятым. Из-за дискретной природы электрического тока шум принципиально неустраним.
В качестве модели помехи широко используют белый шум, для которого частотный спектр является сплошным и равномерным на всех частотах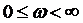 
(односторонний спектр, используемый в технических расчетах).
Даже в отдельных узлах ИС имеет место несколько источников помех. Обычно их объединяют в один эквивалентный источник помех, включаемый на вход того или иного узла.
Будем рассматривать аддитивную смесь (сумму) помехи (шума) и полезного сигнала, включаемую на вход рассматриваемого узла, принимая его характеристики линейными как для помехи, так и для сигнала.
С амплитудной модуляцией
Структурная схема одного из 8 измерительных каналов с амплитудной модуляцией (АМ) аппаратуры 8АНЧ-23 приведена на рис. 3.1.
Рис. 3.1. Структурная схема приема АМ сигнала
При тональной АМ на выходе канала в отсутствие шума сигнал на выходе будет иметь вид: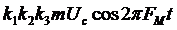 
,
а его эффективное значение равно
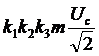, (3.1)
где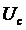 
– амплитуда немодулированного гармонического переносчика (сигнала);
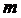– коэффициент АМ ( 
).
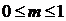Мощность шума на выходе измерительного канала
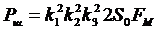, (3.2)
где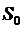 
– спектральная плотность шума 
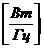. Физически 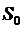есть мощность шума в полосе 
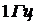, которая не изменяется во всем диапазоне частот. Коэффициент 2 в (3.2) обусловлен удвоением спектральной плотности шума в детекторе.
С учетом (3.2) эффективное напряжение шума, выделяемое на нагрузке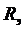 
, составит
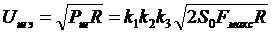. (3.3)
Определяя эффективное напряжение полезного сигнала через его мощность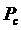 
на нагрузке 
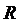из выражений (3.1) и (3.3) и приняв 
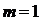, находим относительную среднеквадратическую погрешность в измерительном канале с АМ:
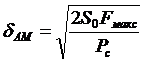. (3.4)
Заметим, что в формуле (3.4) отсутствуют коэффициенты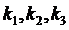 
, а также сопротивление нагрузки 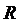. Поэтому в дальнейшем при вычислении погрешностей будем принимать 
, 
.
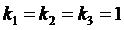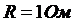С частотной модуляцией
Структурная схема приема ЧМ колебаний приведена на рис. 3.2. Под действием шума изменяются амплитуда и частота гармонического переносчика. Изменение амплитуды исключается введением ограничителя.
Рассмотрим компоненту входного шума в полосе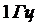 
на частоте 
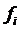с амплитудой 
.
 |
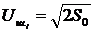Рис. 3.2. Схема приема ЧМ колебаний
Как и ранее, будем считать, что на входе демодулятора ЧМ колебаний напряжение сигнала много больше напряжения шума. Из векторной диаграммы рис. 3.3 найдем
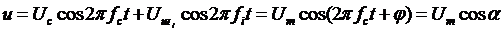, (3.5)
где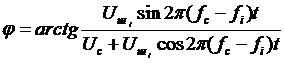 
; (3.6)
при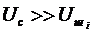 
из (3.6) получим
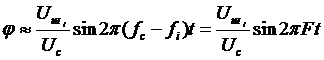, (3.7)
где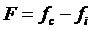 
.
 | |||
 | |||
Рис. 3.3. Векторная Рис. 3.4. Спектр шума
диаграмма аддитивной на выходе частотного
смеси сигнала и шума детектора
При изменении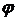 
(рис. 3.3) амплитуда сигнала 
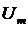остается неизменной и равной напряжению ограничения. Будем считать коэффициент передачи ограничителя равным единице. Тогда круговую частоту на выходе частотного детектора (ЧД), настроенного на среднюю частоту 
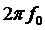, определим как
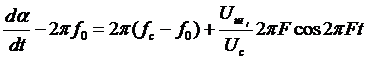
или
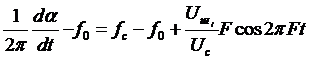, (3.8)
где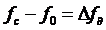 
– девиация частоты, определяет полезный сигнал на выходе ЧД, а оставшаяся часть (3.8) – шумовую компоненту, эффективное напряжение которой в полосе 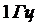на выходе ЧД равно:
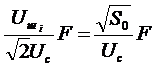. (3.9)
Как и в детекторе АМ колебаний в ЧД спектральная плотность шума удваивается. Поэтому спектральная плотность шумов на выходе ЧД с учетом (3.8) и (3.9) будет
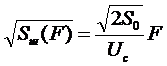, (3.10)
т.е. имеем треугольный спектр шума на выходе ЧД. График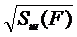 
показан на рис. 3.4. Используя (3.10), находим эффективное напряжение в полосе пропускания фильтра НЧ от нуля до 
:
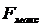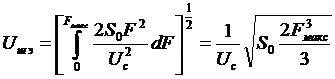. (3.11)
Эффективное напряжение сигнала на выходе ЧД пропорционально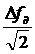 
, где 
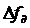– девиация частоты сигнала.
Отношение эффективных напряжений сигнал/шум на выходе фильтра НЧ равно:
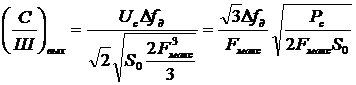, (3.12)
где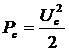 
.
Используя определение индекса модуляции 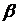в (2.7), из соотношения (3.12) можно найти шумовую относительную среднеквадратическую погрешность для канала с ЧМ:
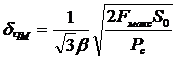. (3.13)
Из соотношений (3.4) и (3.13) находим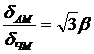 
.
Это уравнение определяет выигрыш ЧМ в отношении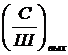 
по сравнению с АМ. Этот выигрыш обеспечивается за счет более широкой частотной полосы канала с ЧМ, что следует из формул Манаева Е.И. (2.9) и (2.10).
Метод накопления
Одним из эффективных и широко применяемых в различных вариантах методов борьбы с помехами является метод накопления. Сущность метода состоит в том, что сигнал или его элементы многократно повторяются. На приеме отдельные образцы сигнала сличаются (обычно суммируются), и так как различные образцы по-разному искажаются помехой в силу независимости последних, то можно восстановить переданный сигнал с большой достоверностью.
В простейшей форме метод накопления часто применяется при телефонном разговоре в условиях плохой слышимости, когда переспрашивают и повторяют одно и то же слово по несколько раз. В случае двоичного кода каждая кодовая комбинация передается по несколько раз. Если вероятность сбоя символов 1 и 0 одинакова, то на приеме решение выносится «по большинству», т. е. воспроизводится символ 1 на данной позиции, когда их число на этой позиции больше числа символов 0, и наоборот, воспроизводится 0, когда число «нулей» больше числа «единиц».
Пример
Переданная комбинация 01001
1-я принятая комбинация 00001
2-я принятая комбинация 11010
3-я принятая комбинация 01101
Воспроизведенная комбинация 01001
Заметим, что можно было бы получить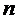 
образцов сигнала не путем их повторения во времени, а путем передачи по независимым каналам, разделенным по частоте, или каким-либо другим способом.
Существуют и другие разновидности метода накопления. К ним, в частности, относится метод синхронного накопления, когда на протяжении посылки берется не один отсчет, а несколько. На приеме эти отсчеты суммируются в накопителе.
Пусть отдельные отсчеты принятого сигнала:
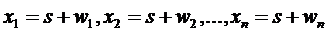. (5.1)
Тогда суммы отсчетов с учетом (5.1):
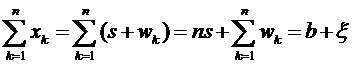. (5.2)
Величина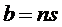 
в выражении (5.2) представляет собой полезный сигнал на выходе приемника. Случайная величина 
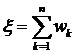представляет собой помеху. Отношение сигнала к помехе на выходе приемника 
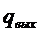равно:
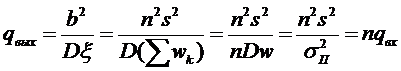. (5.3)
Заметим, что здесь в отличие от принятых обозначений в главе 3 под отношением сигнала к помехе понимается отношение их мощностей.
Мы полагаем, что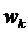 
не коррелированны и имеют одинаковое распределение, 
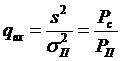– отношение сигнала к помехе на входе приемника, 
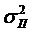– дисперсия случайного процесса.
Таким образом, при описанных условиях накопление отсчетов сигнала (5.3) позволяет увеличить отношение сигнала к помехе на выходе приемника в 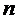раз. Суть дела сводится к тому, что мощность сигнала при суммировании растет пропорционально 
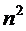(складываются напряжения), а мощность помехи – пропорционально 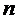(суммируются мощности). Поэтому отношение сигнала к помехе увеличивается в 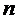раз, если отсчеты помехи независимы. При наличии корреляции между значениями помехи этот выигрыш будет меньше.
Метод накопления можно осуществить, беря не сумму отсчетов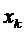 
, а интеграл непрерывно изменяющейся функции 
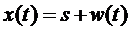за время 
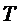, равное длительности сигнала:
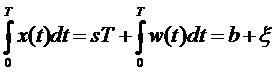. (5.4)
Если спектр помехи равномерен в достаточно широкой полосе частот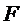 
, т. е. интервал корреляции помехи 
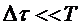, то можно показать, что отношение сигнала к помехе на выходе интегратора
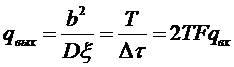. (5.5)
Из выражений (5.4) и (5.5) следует, что выигрыш, получаемый при интегрировании, тем больше, чем больше отношение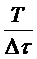 
(чем меньше помеха коррелированна с сигналом). Описанный способ приема называется интегральным.
Согласованный фильтр
Существует большой класс задач, в которых требуется обнаружить сигнал, если форма его известна. К таким сигналам, в первую очередь, относятся дискретные двоичные сигналы. В этих случаях важным параметром, характеризующим качество обнаружения, является отношение сигнала к помехе. Линейный фильтр, максимизирующий это отношение, называется оптимальным согласованным фильтром.
Пусть на входе фильтра действует сумма сигнала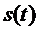 
и помехи 
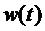, т. е. колебание
.
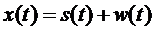Полезный сигнал 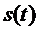рассматривается не как случайный процесс, а как функция известной формы со спектральной плотностью
,
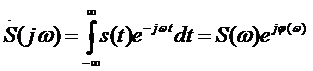где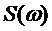 
и 
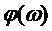– амплитудный и фазовый спектры сигнала. Помеху будем считать стационарным случайным процессом типа белого шума с равномерной двухсторонней спектральной плотностью
.
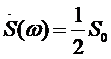Коэффициент передачи линейного фильтра запишем в виде
.
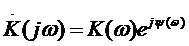Сигнал на выходе фильтра, очевидно, равен сумме полезного сигнала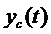 
и помехи 
:
.
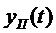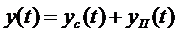Полезный сигнал на выходе можно записать в виде
.
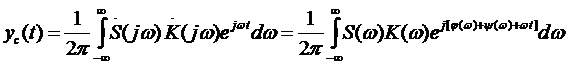Пиковая мощность сигнала в некоторый момент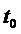 
будет равна:
,
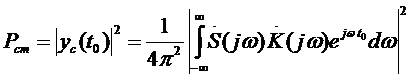а мощность помехи
.
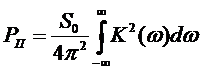Тогда превышение сигнала над помехой в момент времени 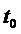будет определяться следующим выражением:
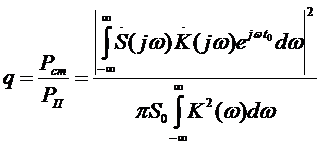. (5.6)
Необходимо найти, каким должен быть коэффициент передачи фильтра, чтобы отношение сигнала к помехе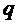 
на его выходе было максимальным. Известно неравенство Буняковского - Шварца:
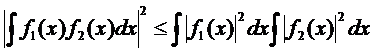. (5.7)
На основании этого неравенства получаем, что при любой характеристике фильтра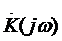 
отношение сигнала к помехе не может превосходить максимального значения:
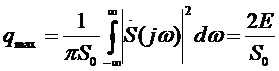, (5.8)
где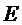 
– полная энергия сигнала. Указанная в равенстве (5.8) максимальная величина 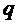достигается в том случае, когда коэффициент передачи фильтра имеет следующее выражение:
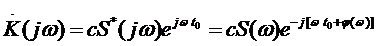, (5.9)
где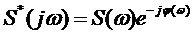 
– функция, комплексно сопряженная со спектром сигнала 
; 
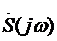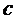– произвольная постоянная.
Выражение (5.9) можно записать в виде двух равенств:
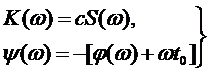, (5.10)
из которых следует, что амплитудно-частотная характеристика согласованного фильтра с точностью до постоянного множителя совпадает с амплитудным спектром сигнала, а фазочастотная характеристика определяется фазовым спектром сигнала 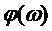и линейной функцией частоты 
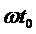. Таким образом, частотная характеристика согласованного фильтра полностью определяется спектром сигнала, "согласована" с ним.
Фаза сигнала на выходе согласованного фильтра с учетом (5.10) будет равна:
.
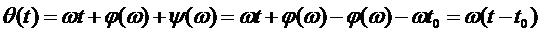При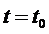 
, т.е. в момент 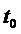, все гармонические составляющие сигнала имеют одинаковую фазу и складываются арифметически, образуя в этот момент пик сигнала на выходе фильтра. Спектральные же составляющие помехи на выходе фильтра имеют случайную фазу. Этим и объясняется доказанное выше положение о том, что согласованный фильтр максимизирует отношение сигнала к помехе на выходе.
В качестве примера рассмотрим построение согласованного фильтра для прямоугольного импульса, заданного в виде:
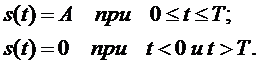
Спектр такого импульса, как известно,
.
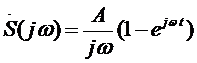На основании (5.9) коэффициент передачи согласованного фильтра будет
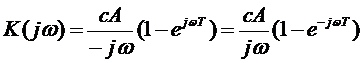. (5.11)
Известно, что умножение на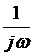 
в частотной области соответствует интегрированию в пределах от 
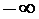до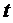 
во временной области, а умножение на 
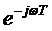соответствует задержке сигнала на время .
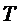Следовательно, фильтр с коэффициентом передачи (5.11) состоит из интегратора И, включающего в себя дополнительно масштабирующий усилитель с коэффициентом усиления 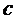, линии задержки на время Т с коэффициентом передачи 
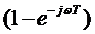и вычитающего устройства В (рис. 5.1, а).
 |
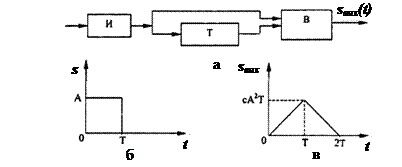Рис. 5.1. Согласованный фильтр для прямоугольного импульса (а), сигнал на его входе (б) и выходе (в)
Сигнал на выходе фильтра имеет форму равнобедренного треугольника (рис. 5.1, в) с основанием 2Т и высотой, равной энергии сигнала сА2Т, т. е.:
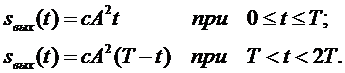
В ряде случаев согласованные фильтры оказываются практически труднореализуемыми. Поэтому часто применяют фильтры, которые согласованы с сигналом только по полосе (квазиоптимальные фильтры). Оптимальная полоса для различных импульсов различна и может быть вычислена без особых трудностей. Так, для фильтра с прямоугольной частотной характеристикой, на который воздействует радиоимпульс прямоугольной формы длительностью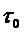 
, оптимальная полоса равна 
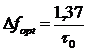. Можно показать, что отношение сигнала к помехе на выходе квазиоптимального фильтра по сравнению с согласованным фильтром уменьшается на величину порядка.
Оптимальная фильтрация
Источник дискретных сообщений характеризуется совокупностью возможных элементов сообщения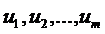 
и вероятностями появления этих элементов на выходе источника 
.
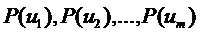В передающем устройстве сообщение преобразовывается в сигнал таким образом, что каждому элементу соответствует определенный сигнал. Обозначим эти сигналы через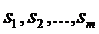 
, а их вероятности на выходе передатчиков (априорные вероятности) соответственно через 
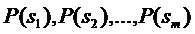. Очевидно, априорные вероятности сигналов 
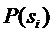равны априорным вероятностям 
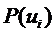соответствующих сообщений 
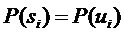. В процессе передачи на сигнал накладывается помеха. Пусть эта помеха имеет равномерный спектр мощности с интенсивностью 
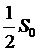. Тогда сигнал на входе можно представить как сумму переданного сигнала и помехи :
.
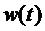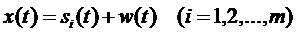В случае, когда априорные вероятности сигналов одинаковы: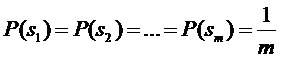 
, можно сформулировать условие оптимального приема (критерий Котельникова):
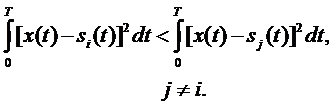
Отсюда следует, что при равновероятных сигналах оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, который имеет наименьшее среднеквадратичное отклонение от принятого сигнала. Если все возможные сигналы равновероятны и имеют одинаковую энергию, оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, взаимная корреляция которого с принятым сигналом максимальна.
6. ЭЛЕМЕНТЫ ТЕОРИИ ИНФОРМАЦИИ
Пропускная способность
Непрерывного канала
Рассмотрим случай, когда помеха в канале действует как аддитивный шум n(t), т.е.
z(t) = y(t) +n(t).
Допустим также, что этот шум – стационарный, имеет нормальный закон распределения и его средняя мощность равна его дисперсии Pш=sN2 (sN2 – дисперсия сигнала помехи). Заметим, что шум с нормальным законом распределения обладает максимальной энтропией, и, следовательно, такой шум создает максимальное воздействие на полезный сигнал.
Определив пропускную способность канала, примем во внимание, что его полоса частот пропускания ограничена пределами от 0 до Fm, а средняя мощность Рc полезного сигнала y(t) выражается через его дисперсию: Pc = sY2.
С учетом ограничения полосы частот пропускания канала спектры частот сигналов y(t), z(t) и n(t) не должны превышать частоты Fm. В этом случае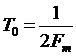 
, и тогда выражение (6.20) можно представить так:
.
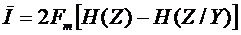В случае аддитивной помехи последнее выражение можно записать как
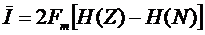, (6.24)
где H(N) – энтропия источника помехи (в нашем случае) с нормальным законом распределения, имеющим вид
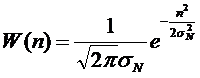. (6.25)
Энтропию такого источника найдем по формуле
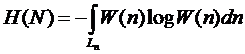. (6.26)
Так как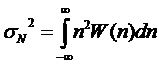 
и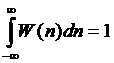 
, из выражения (6.26) с учетом (6.25) получим
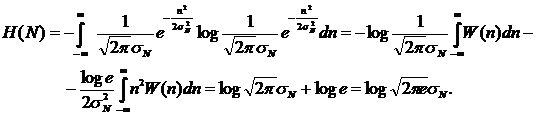(6.27)
Пропускную способность рассматриваемого канала можно найти с учетом (6.24) и (6.27) в виде
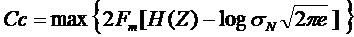. (6.28)
Поскольку Fm и sN в нашем случае заданы, то выражение, стоящее в квадратных скобках, будет наибольшим, если энтропия выходных сигналов канала H(Z) будет максимальной. Так как средние мощности полезного сигнала y(t) и шума n(t) ограничены, то их аддитивная смесь на выходе канала z(t) будет также име<