Методические указания к выполнению лабораторных работ

Методические указания к выполнению лабораторных работ

по курсу: "Основы дискретной математики"

для студентов специальностей 091401, 092401

«Системы управления и автоматика»,

«Телекоммуникационные системы и сети»

Рассмотрен на заседании кафедры автоматики и телекоммуникаций.

Протокол № 11

от « 22 » октября 2010 р.

Утвержден на заседании научно-издательского совета ДонНТУ

Протокол № ___

от «___»___________2010 р.

Донецк, ДонНТУ 2010

УДК 681.3.07

Методические указания к лабораторным работам по курсу "Основы дискретной математики" для студентов специальностей 091401, 092401 «Системы управления и автоматика», «Телекоммуникационные системы и сети» / доц. Жукова Н.В., ас. Зайцева Э.Е. – Донецк, ДонНТУ. 2010. – 45 с.

Методические указания содержат лабораторные работы по основным разделам курса ОДМ и предназначены для студентов специальностей 091401, 092401 «Системы управления и автоматика», «Телекоммуникационные системы и сети».

Составитель доц. Жукова Н.В., ас. Зайцева Э.Е.

Рецензент доц. Ф-ту КНТ каф. АСУ Светличная В.А.

доц. Ф-ту КИТА каф. ЭТ Тарасюк В.П.

Ответственный за выпуск доц. Бессараб В.И.

Содержание

Лабораторная работа №1.

Множества, операции над множествами…………………...............……………4

Лабораторная работа №2.

Алгебра высказываний……………………………….................….…...................9

Лабораторная работа №3.

Минимизация булевых функций. Логические схемы……..……………………17

Лабораторная работа №4.

Конечные автоматы с памятью..…………………………………………………32

СПИСОК ЛИТЕРАТУРЫ…………………………………………………………45

Лабораторная работа № 1

Тема: «Множества, основные операции над множествами»

Цель: Приобретение практических навыков работы с множествами

1.1. Теоретические сведения [1].

Операции над множествами

Опишем основные способы получения новых множеств из уже имеющихся. Эти способы называются операциями над множествами.

Объединение множеств

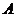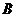Объединением множеств и называется множество, которое обозначается 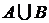(иногда 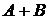) и состоящее из всех тех и только тех элементов, которые принадлежат множеству или множеству .

Приведем графическую иллюстрацию операции объединения двух множеств:

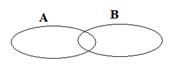
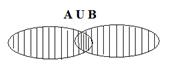
Выражение 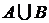читается: «объединение множества и множества ». Часто операцию объединения двух множеств записывают в виде:

,

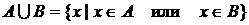который возможно использовать, учитывая, что множество элементов 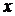– это множество «всех тех и только тех элементов, которые принадлежат множеству или множеству ».

Пересечение множеств

Пересечением множеств и называется множество, которое обозначается 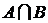(иногда 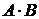) и состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств и .

Приведем графическую иллюстрацию операции пересечения двух множеств:

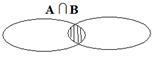
Выражение 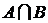читается: «пересечение множества и множества ».

Часто операцию пересечения двух множеств записывают в виде:

,

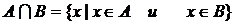который возможно использовать, учитывая, что множество элементов 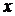– это множество «всех тех и только тех элементов, которые принадлежат каждому из множеств и ».

Разность множеств

Рассмотрим операцию над множествами, которая определяется только для двух множеств.

Разностью множеств и называется множество, которое обозначается 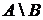(иногда 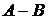) и состоящее из всех тех и только тех элементов множества , которые не является элементами множества .

Приведем графическую иллюстрацию операции разности двух множеств:

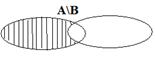
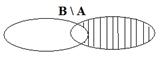
Выражение 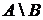читается: «разность множества и множества ».

Часто операцию разности двух множеств 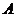и 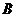записывают в виде:

,

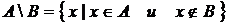который возможно использовать, учитывая, что множество элементов 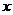– это множество «всех тех и только тех элементов множества , которые не являются элементами множества ».

Симметрическая разность

Симметрической разностью множеств и называется множество, которое обозначается 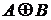(иногда 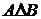) и определенное следующим образом:

.

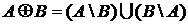Приведем графическую иллюстрацию операции симметрической разности двух множеств:

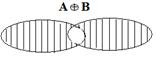
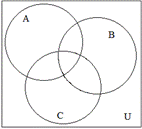
Пример. Записать с помощью операций над множествами выражение для множества, соответствующего заштрихованной области диаграммы:

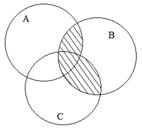
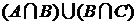► или . ◄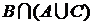

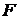Пример. С помощью графической интерпретации изобразить множество , если 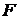образовано множествами , и :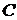

.

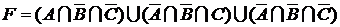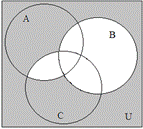
► Изобразим множества , и 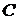на диаграмме Эйлера-Венна, как показано на рисунке ниже.

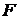Множество есть объединение трех множеств, 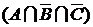, 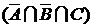и 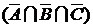. Рассмотрим множество 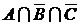. Его элементами являются элементы множества , которые не принадлежат и не принадлежат 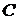. Аналогично, множество 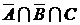состоит из элементов 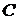, не принадлежащих или . Элементы множества 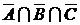– есть элементы 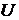, не принадлежащие ни , ни , ни 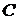. Таким образом, множество 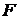на диаграмме Эйлера-Венна имеет вид (заштрихованным областям соответствует серый цвет):

◄

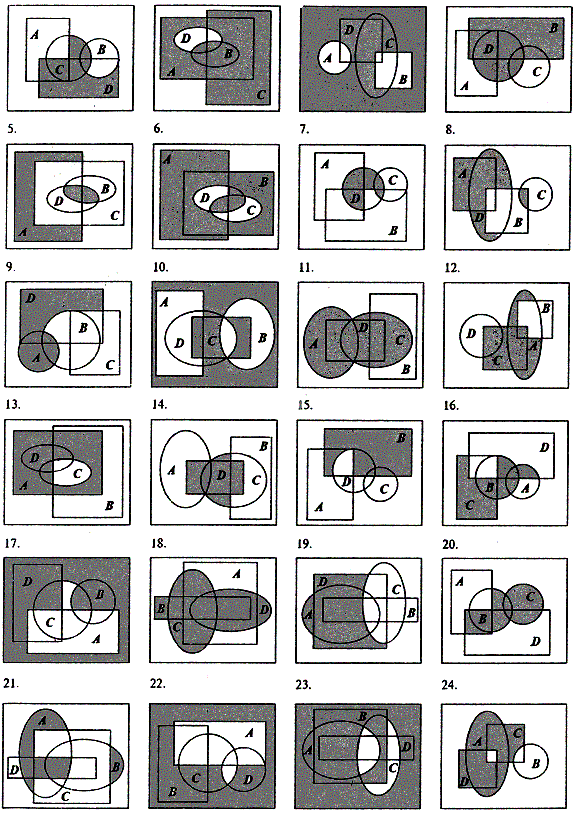
1.2. Задание.

Ниже приведены диаграммы Виенна. Представьте заштрихованную и отдельно незаштрихованную области максимально компактными аналитическими выражениями, в которых бы использовались минимальное количество логических операций и букв. Результаты проверьте по таблицам истинности.

1.3. Контрольные вопросы

1.3.1. Дайте определение конечного множества, элементов множества.

1.3.2. Какие существуют основные способы задания множества?

1.3.3. Какие множества называются равными? Что такое подмножество?

1.3.4. Назовите основные операции над множествами, какой наглядный инструмент используется для иллюстрации операций над множествами?

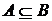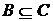1.3.5. Докажите свойство если и , то .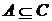

1.3.6. Перечислите свойства операций над множествами, докажите , .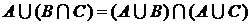

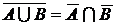1.3.7. Дайте определение прямому (декартовому) произведению множеств;

1.3.8. Записать с помощью операций над множествами выражение для множества, соответствующего закрашенной области диаграммы:

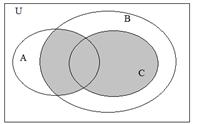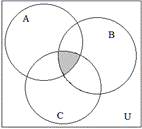
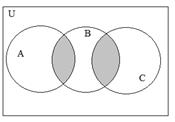
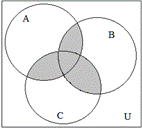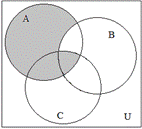1.3.9. С помощью графической интерпретации изобразить множество 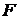, если 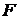образовано множествам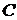и , , и :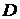

;

;

;

;

;

.

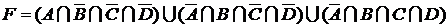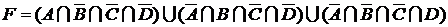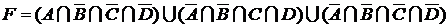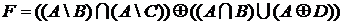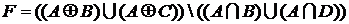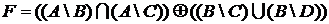1.3.10. Доказать тождества

;

;

;

;

;

;

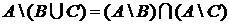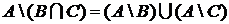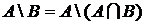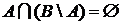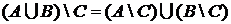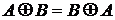Лабораторная работа № 2

Тема: «Алгебра высказываний»

Цель: Приобретение практических навыков работы с алгеброй логики высказываний.

2.1 . Теоретические сведения [1].

Таблицы истинности

Каждая формула алгебры обладает свойством превращаться в высказывание при фиксации в ней значений всех высказывательных переменных, т. е. если мы зафиксируем в формуле значения всех высказывательных переменных, то, пользуясь определениями логических операций, мы можем вычислить значение истинности формулы.

Таблица истинности формулы алгебры высказываний содержит столько строк, сколько всевозможных наборов значений истинности переменных можно образовать. Так как каждая высказывательная переменная может принимать только два значения (0 и 1), то в случае 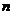переменных таблица истинности содержит 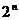строк.

При построении таблицы истинности наборы значений переменных располагают сверху вниз в лексикографическом порядке (каждый набор понимают как двоичную запись неотрицательного целого числа и располагают в порядке возрастания от (000 … 0) до (111 … 1).

Если у вас возникают трудности с использованием двоичной системы счисления, можно применять метод «последовательного половинного деления столбцов» – столбец первой переменной делят пополам и заполняют верхнюю половину нулями, а нижнюю половину – единицами, затем каждую половину второго столбца делят пополам и опять заполняют полученные половины нулями и единицами, и т. д. Затем в соответствии с порядком действий последовательно заполняют столбцы значений подформул, из которых образуется формула. Последним заполняется столбец значений истинности формулы.

Пример.Построить таблицу истинности формулы: .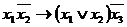

1. Определить порядок действий в формуле:

.

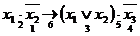2. Пользуясь определениями операци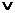й –, &, и 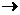, заполним таблицу:

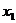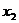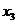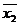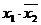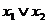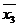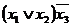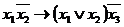Равносильные преобразования и упрощения формул

Ключом к решению примеров на равносильные преобразования и упрощения формул являются 19 основных равносильностей булевой алгебры высказывания (теорема 2.2) [1], поэтому первым шагом при решении таких примеров является переход к булевым операциям с помощью формул:

,

~ .

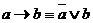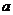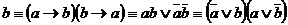Условное решение примера зависит от умелого, эффективного применения основных равносильностей. Следует иметь в виду, что буквы, использованные при записи основных равносильностей, могут означать как символы высказывательных переменных, так и формулы алгебры высказываний, т. е. основная равносильность 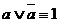означает, в частности, что , , .

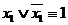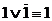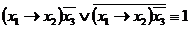Полезными при решении примеров на упрощение формул являются законы полупоглощения:

1) 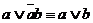; 1’) ;

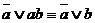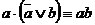2) ; 2’) ,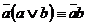

которые мы сейчас докажем.

► .

.◄

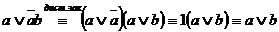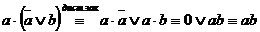Пример.С помощью равносильных преобразований упростить формулу .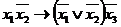

►

◄

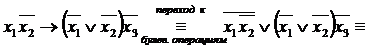
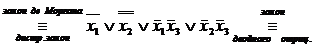
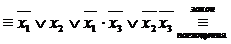
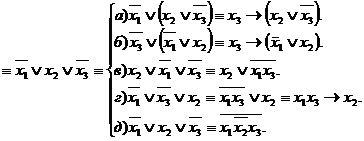Замечание.Любую запись а) - д) можно считать ответом.

Следующий тип параметров – доказательство равносильности двух заданных формул с помощью равносильных преобразований. Существует три основных схемы решения таких примеров. Каждая из них предполагает выполнение перехода к булевым операциям в исходных формулах.

Далее, по первой схеме предполагается, начиная с левой формулы, провести цепочку равносильных преобразований, завершив ее на правой формуле.

Вторая схема – зеркальное отражение первой.

Третья схема предполагает проведение параллельных цепочек равносильных преобразований левой и правой формул до тех пор, пока в этих цепочках не обнаружится совпадение каких-то звеньев (одного звена верхней цепочки с одним звеном нижней).

Пример.Доказать, что .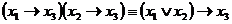

►Перейдем к булевым операциям

.

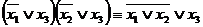1-я схема.

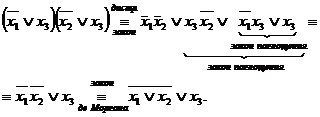
2-я схема

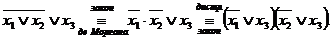
3-я схема

◄

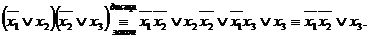
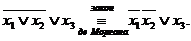Замечание. Следует иметь в виду, что среди примеров на доказательство равносильности формул есть примеры с отрицательным ответом. В этом случае ни одна из схем не приводят к получению ответа. Однако, неудача при использовании схем 1 – 3 может говорить и о недостаточно высокой технике равносильных преобразований. В случае неудачных попыток применения схем 1 – 3 следует для обеих формул построить таблицы истинности. Совпадение столбцов значений формул будет означать их равносильность, а несовпадение – неравносильность.

Лабораторная работа № 3

Тема: «Минимизация булевых функций. Логические схемы»

Цель: Приобретение практических навыков работы с методами минимизации булевых функций.

3.1. Теоретические сведения [1].

Минимальные формы

Как было показано в [1], любая булева функция представима в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Более того, такое представление является первым шагом перехода от табличного задания функции к ее аналитическому выражению. В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получается на основе принципа двойственности [1].

Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний). Такие формы называют минимальными. При каноническом синтезе предполагается, что на входы схемы подаются как сигналы 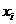, так и их инверсий .

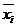Формула, представленная в дизъюнктивной нормальной форме, упрощается многократными применением операции склеивания 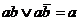и операции поглощения 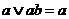и 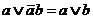(дуальные тождества для конъюнктивной нормальной формы имеют вид: 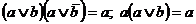и 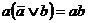). Здесь под 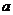и 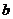можно понимать любую формулу булевой алгебры. В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются уже невозможными, т.е. получаем тупиковую форму.

Среди тупиковых форм находится и минимальная дизъюнктивная форма, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма является минимальной, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.

Пусть, например, функция задана в совершенной нормальной дизъюнктивной форме:

.

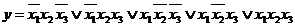Группируя члены и применяя операцию склеивания, имеем .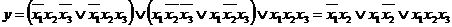

При другом способе группировки получим:

.

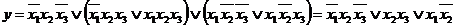Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, так как 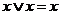). В первом случае таким членом может быть 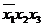. Тогда 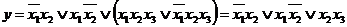. Добавив член 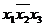, получим: 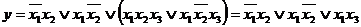. Перебрав все возможные варианты, можно убедиться, что две последние формы являются минимальными.

Работа с формулами на таком уровне подобна блужданию в потемках. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать некоторые графические и аналитические представления и специально разработанную для этой цели символику.

Многомерный куб

Каждой вершине 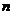-мерного куба можно поставить в соответствие конституенту единицы. Следовательно, подмножество отмеченных вершин является отображением на 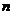-мерном кубе булевой функции от 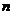переменных в совершенной дизъюнктивной нормальной форме. На рис. 3.1 показано такое отображение для функции из п.3.7.

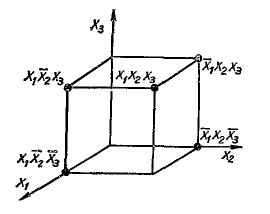
Рис.3.1 Отображение на трехмерном кубе функции, представленной в СДНФ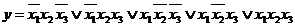

Для отображения функции от 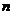переменных, представленной в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитермами и элементами 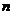-мерного куба.

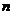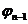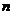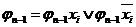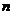Минитерм ( -1)-го ранга можно рассматривать как результат склеивания двух минитермов -го ранга (конституент единицы), т.е. , На -мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координаты 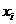, соединяющим эти вершины, ребром (говорят, что ребро покрывает инцидентные ему вершины). Таким образом, минитермам ( 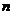-1)-го порядка соответствуют ребра 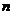-мерного куба. Аналогично устанавливается соответствие минитермов ( 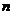-2)-го порядка - граням 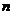-мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).

Элементы 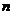-мерного куба, характеризующиеся 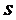измерениями, называют 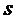-кубами. Так, вершины являются 0-кубами, ребра – 1-кубами, грани – 2-кубами и т.д. Обобщая приведенные рассуждения, можно считать, что минитерм ( 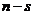)-го ранга в дизъюнктивной нормальной форме для функции 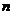переменных отображается 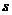-кубом, причем каждый 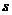-куб покрывает все те 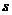-кубы низшей размерности, которые связаны с его вершинами. В качестве примера на рис. 3.2 дано отображение функции трех переменных. 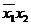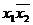Здесь минитермы и соответствуют 1-кубам ( 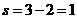), а минитерм 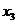отображается 2-кубом ( ).

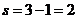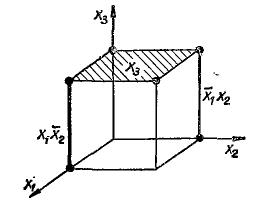
Рис.3.2 Покрытие функции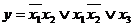

Итак, любая дизъюнктивная нормальная форма отображается на 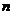-мерном кубе совокупностью 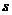-кубов, которые покрывают все вершины, соответствующие конституентам единицы (0-кубы). Справедливо и обратное утверждение: если некоторая совокупность 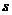-кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим 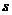-кубам минитермов является выражение данной функции в дизъюнктивной нормальной форме. Говорят, что такая совокупность 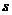-кубов (или соответствующих им минитермов) образует покрытие функции.

Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число 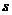-кубов которого было бы поменьше, а их размерность 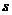- побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием. Например, для функции 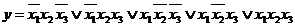покрытие на рис. 3.3 соответствует минимальным формам 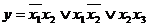и .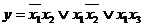

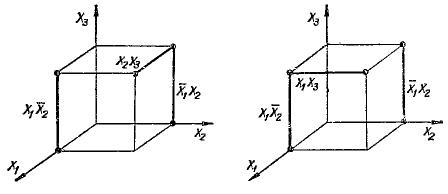
Рис. 3.3 Покрытия функции .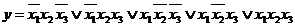

слева – 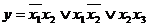; справа –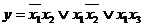

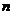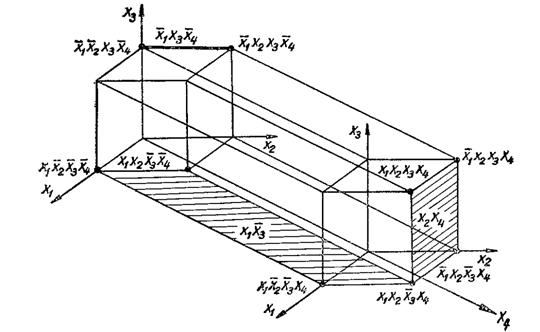
Отображение функции на -мерном кубе наглядно и просто при 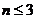. Четырехмерный куб можно изобразить, как показано на рис. 3.4, где отображены функция четырех переменных и ее минимальное покрытие, соответствующее выражению 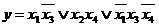. Использование этого метода при 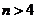требует настолько сложных построений, что теряется все его преимущества.

Рис. 3.4 Отображение функции на четырехмерном кубе

Карты Карно

В другом методе графического отображения булевых функций используются карты Карно, которые представляют собой специально организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. На рис. 3.5 показаны карты Карно для двух, трех, четырех переменных.

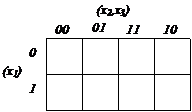Рис. 3.5 Карты Карно для двух, трех и четырех переменных

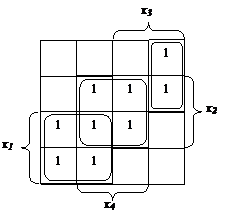
Как и в обычных таблицах истинности, клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки). Например, на рис. 3.6, а показана карта Карно для функции, отображение которой на четырехмерном кубе дано на рис. 3.4. Для упрощения строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.

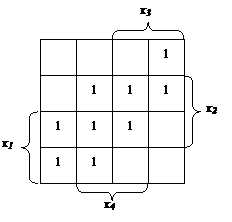а б

Рис. 3.6 Отображение на карте Карно функции четырех переменных

(а) и ее минимального покрытия (б)

Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно s-кубу соответствует совокупность 2 соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике (с учетом соседства противоположных краев карты). Поэтому все положения, изложенные в выше (см. п. многомерный куб), справедливы для карт Карно. Так, на рис. 3.6, б показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме 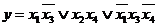рассматриваемой функции.

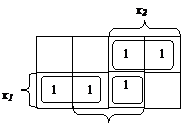
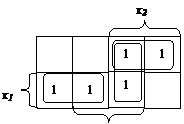
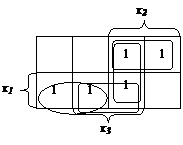
Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие s-куб, дают минитер (n–s)-го ранга, в который входят те (n–s) переменные, которые сохраняют одинаковые значения на этом s-кубе, причем значении 1 соответствуют сами переменные, а значениям 0 – их отрицания. Переменные, которые не сохраняют свои значения на s-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в дизъюнктивной нормальной форме (крайняя правая является минимальной) (рис. 3.7).

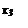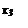Рис. 3.7 Способы считывания с карты Карно дизъюнктивной нормальной формы булевой функции (слева направо: ; ;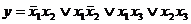

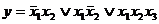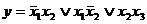
Пример.Получить минимальные формы для функции

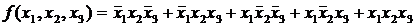
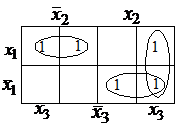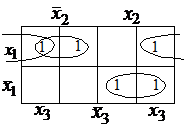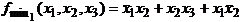
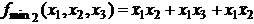
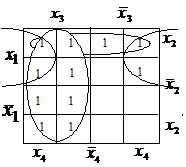
Пример.Получить минимальную форму для функции, заданной на карте.

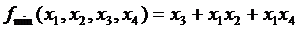
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае четырех переменных. Для отображения функций пяти переменных используется две карты Карно на четыре переменные, а для функции шести переменных – четыре таких карты. При дальнейшем увеличении числа переменных карты Карно становятся практически непригодными.

Известные в литературе карты Вейча отличаются только другим порядком следования наборов значений переменных и обладают теми же свойствами, что и карты Карно.

Комплекс кубов

Несостоятельность графических методов при большом числе переменных компенсируется различными аналитическими методами представления булевых функций. Одним из таких представлений является комплекс кубов, использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой.

Комплекс кубов К(у) функции 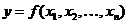определяется как объединение множеств К^s(у) всех ее s-кубов (s=0.1,…,n), т. е. 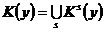, причем некоторые из К^s(у) могут быть пустыми. Для записи s-кубов и минитермов функции от n переменных используются слова длины n, буквы которых соответствуют всем n переменным. Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен единице (1 для 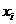и 0 для 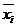). Не входящие в минитерм переменные являются свободными и обозначаются через 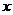. Например, 2-куб функции пяти переменных, соответствующий минитерму 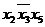запишем как ( 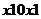). 0-кубы, соответствующие конституентам единицы, представляются наборами значений переменных, на которых функция равна единице. Очевидно, в записи s-куба всегда имеется s свободных переменных. Если все n переменных свободны, что соответствует n-кубу, то это означает тождественность единице рассматриваемой функции. Таким образом, для функций, не равных тождественно единице 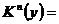Ø.

Множество всех s-кубов 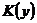записывается как совокупность слов, соответствующих каждому s-кубу. Для удобства будем располагать слова s-кубов в столбцы, а их совокупность заключать в фигурные скобки. Например, комплекс кубов, соответствующий представлению функции на трехмерном кубе (рис. 3,10а), выражается как 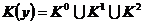, где