Построение мультипликативной модели временного ряда.

Имеются поквартальные данные об объеме выпуска товара фирмой за последние три года, представленные в таблице 4.

Шаг 1. Проведем выравнивание исходных уровней ряда мето­дом скользящей средней. Методика, применяемая на этом шаге, полностью совпадает с методикой аддитивной модели. Результаты расчетов оценок сезонной компоненты представлены в таблице 11.

Таблица 11 - Расчет оценок сезонной компоненты в мультипликативной модели.

Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользя­щие средние (графа 6 таблицы 10). Используем эти оценки для расче­та значений сезонной компоненты S (таблица 12). Для этого най­дем средние за каждый квартал оценки сезонной компоненты . Взаимопогашаемость сезонных воздействий в мультипликатив­ной модели выражается в том, что сумма значений сезонной ком­поненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла (год) равно 4 (четыре квартала).

Таблица 12 - Расчет сезонной компоненты в мультипликативной модели.

Имеем:

.

Определим корректирующий коэффициент: .

Определим скорректированные значения сезонной компо­ненты, умножив ее средние оценки на корректирующий коэффи­циент k.

где ,

Проверим условие равенства 4 суммы значений сезонной компоненты:

.

Получим следующие значения сезонной компоненты:

I квартал: ;

II квартал:

III квартал: ;

IV квартал: .

Занесем полученные значения в таблицу 13 для соответствующих кварталов каждого года (графа 3).

Шаг 3. Разделим каждый уровень исходного ряда на соответ­ствующие значения сезонной компоненты. Тем самым мы полу­чим величины (графа 4 таблицы 13), которые содержат только тенденцию и случайную компоненту.

Таблица 13 - Расчет выровненных значений Τ и ошибок Ε в мультипликативной модели.

Шаг 4. Определим компоненту T в мультипликативной моде­ли. Для этого рассчитаем параметры линейного тренда, исполь­зуя уровни . Уравнение тренда имеет следующий вид:

,

.

Подставляя в это уравнение значения t = 1, ..., 16, найдем уровни T для каждого момента времени (графа 5 таблицы 13). График уравнения тренда приведен на рисунке 5.

Шаг 5. Найдем уровни ряда по мультипликативной модели, умножив уровни T на значения сезонной компоненты для соот­ветствующих кварталов. Графически значения представле­ны на рисунке 5.

Шаг 6. Расчет ошибки в мультипликативной модели произво­дится по формуле:

,

Численные значения ошибки приведены в графе 7 таблицы 13.

Для сравнения мультипликативной модели с другими моделями временного ряда можно использовать величину абсолютной ошибки:

,

Следовательно, ошибка ε мультипликативной модели составит:

.

Таким образом, доля объясненной дисперсии уровней ряда в мультипликативной модели составит .

Прогнозирование

Для прогнозирования из двух рассмотренных моделей необходимо выбрать ту, у которой ошибка ε наименьшая. Следовательно, при прогнозировании будет использоваться аддитивная модель, так как .

Таким образом, прогнозное значение уровня временного ряда в аддитив­ной модели есть сумма трендовой и сезонной компонент.

Объем товаров, выпущенного фирмой в течение первого по­лугодия ближайшего следующего, т. е. четвертого года, рассчитывается как сумма объемов выпущенных товаров в I и во II кварталах четвертого года, соответственно и . Для определения трендовой компоненты воспользуемся уравнением тренда:

.

Получим:

;

.

Значения сезонной компоненты равны: (I квартал); (II квартал). Таким образом,

;

.

Прогноз объема выпуска товаров фирмой на первое полу­годие 2006 года составит:

усл.ед.

Следует отметить, что для осуществления прогноза по мультипликативной модели, прогнозные значения F определяются как:

.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ЗАДАНИЕ №1 ЛИНЕЙНЫЙ ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

На основе данных, приведенных в таблицах Приложения А и соответст­вующих Вашему варианту, требуется:

1. Построить уравнение линейной парной регрессии одного при­знака от другого. Один из признаков, соответствующих Ваше­му варианту, будет играть роль факторного 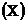, другой - ре­зультативного 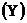. Причинно-следственные связи между при­знаками установить самим на основе экономического анализа. Пояснить смысл параметров уравнения.

2. Рассчитать линейный коэффициент парной корреляции и ко­эффициент детерминации. Сделать выводы.

3. Оценить статистическую значимость параметров регрессии и коэффициента корреляции с уровнем значимости 0,05.

4. Выполнить прогноз ожидаемого значения признака-результата Y при прогнозном значении признака-фактора X, составляющим 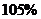от среднего уровня X. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.

5. Дать оценку полученного уравнения с помощью общего F-критерия Фишера.

6. Самостоятельно дополнительно определить параметры 2 функций, оценить их качество.

ЗАДАНИЕ № 2 МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ

На основе данных, приведенных в Приложении А и соответст­вующих Вашему варианту, требуется:

1. Построить уравнение множественной регрессии. Для этого, ос­тавив признак-результат тем же выбрать несколько признаков-факторов из таблицы 1 Приложения А (границы их наблюдения должны совпадать с границами наблюдения признака-результата, соот­ветствующих Вашему варианту). При выборе факторов нужно руководствоваться как экономическим содержанием, так и формальными подходами (например, матрица парных коэффи­циентов корреляции). Пояснить смысл параметров уравнения.

2. Рассчитать частные коэффициенты эластичности.

3. Определить стандартизованные коэффициенты регрессии (β-коэффициенты).

4. На основе полученных результатов сделать вывод о силе связи результата с каждым из факторов.

5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать вы­воды.

6. Дать оценку полученного уравнения с помощью общего F-критерия Фишера.

ПРИЛОЖЕНИЕ А

Вариант 1				Вариант 2
№ наб-люде-ния	Собственные оборотные средства, млн. руб.	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.		№ наб-люде-ния	Собственные оборотные средства, млн. руб.	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.
Вариант 3				Вариант 4
№ наб-люде-ния	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.		№ наб-люде-ния	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.
			20,33					20,46
			20,04					20,07
			19,87					20,23
			20,48					20,26
			20,13					20,28
			20,26					20,52
			19,89					20,28
			19,92					19,97
			19,78					19,97
			20,23					19,57
			20,46					19,94
			20,07					20,29
			20,23					20,83
			20,26					19,59
			20,28					19,76
			20,52					20,19
			20,28					20,66
			19,97					19,95
			19,97					20,61
			19,57					20,03
			19,94					19,78
			20,29					20,22
			20,83					19,78
			19,59					20,09
			19,76					20,13
Вариант 5				Вариант 6
№ наб-люде-ния	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.	Курсовая цена акции, руб.		№ наб-люде-ния	Дебиторская задолженность по результатам деятельности, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.	Курсовая цена акции, руб.
А					А
		20,33					20,46
		20,04					20,07
		19,87					20,23
		20,48					20,26
		20,13					20,28
		20,26					20,52
		19,89					20,28
		19,92					19,97
		19,78					19,97
		20,23					19,57
		20,46					19,94
		20,07					20,29
		20,23					20,83
		20,26					19,59
		20,28					19,76
		20,52					20,19
		20,28					20,66
		19,97					19,95
		19,97					20,61
		19,57					20,03
		19,94					19,78
		20,29					20,22
		20,83					19,78
		19,59					20,09
		19,76					20,13
Вариант 7				Вариант 8
№ наб-люде-ния	Собственные оборотные средства, млн. руб.	Балансовая прибыль, млн. руб.	Дебиторская задолженность по результатам деятельности, млн. руб.		№ наб-люде-ния	Балансовая прибыль, млн. руб.	Дивиденды, начисленные по результатам деятельности, млн. руб.	Курсовая цена акции, руб.
							19,97
							19,97
							19,57
							19,94
							20,29
							20,83
							19,59
							19,76
							20,19
							20,66
							19,95
							20,61
							20,03
							19,78
							20,22
							19,78
							20,09
							20,13
							20,56
							20,51
							19,71
							20,1
							20,32
							20,37
							20,03

ЗАДАНИЕ №3 ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ

Задание:
1. Построить автокорреляционную функцию данного временного ряда и коррелограмму.
2. Сделать выводы относительно структуры временного ряда.
3. Построить аддитивную и мультипликативную модели временного ряда.
4. Оценить качество моделей и выбрать лучшую.
5. Выполнить прогноз по лучшей модели на 2015 год
представив его в расчетной форме и графически.

Наши рекомендации

Вариант 1								Вариант 2
Динамика выручки торгового предприятия, млн.руб.				Динамика выручки торгового предприятия, млн.руб.
год	квартал	У, млн. руб.						год	квартал	У, млн. руб.
		26,4								126,4
		21,3								121,3
		18,3								118,3
		21,5								121,5
		38,5								138,5
		34,2								134,2
		27,4								127,4
		32,5								132,5
		49,5								149,5
		48,1								148,1
		32,1								132,1
		45,8								145,8
		56,4								156,4
		50,3								150,3
		38,2								138,2
		51,3								151,3
		69,3								169,3
		60,8								160,8
		55,1								155,1
		69,7								169,7
		85,4								185,4
		75,1								175,1
		62,3								162,3
		57,3								157,3
Вариант 3								Вариант 4
Динамика выручки торгового предприятия, млн.руб.				Динамика выручки торгового предприятия, млн.руб.
год	квартал	У, млн. руб.						год	квартал	У, млн. руб.
		26,4								246,4
		29,3								299,3
		18,3								188,3
		21,5								261,5
		38,5								328,5
		34,2								394,2
		35,8								365,8
		32,5								332,5
		49,5								419,5
		48,1								478,1
		32,1								382,1
		51,4								521,4
		56,4								596,4
		50,3								550,3
		38,2								358,2
		51,3								541,3
		69,3								669,3
		53,8								693,8
		55,1								555,1
		69,7								619,7
		83,7								813,7
		75,1								755,1
		62,3								672,3
		62,1								632,1
Вариант 5								Вариант 6
Данные о заготовках леса, тыс. м куб.					Данные о заготовках леса, тыс. м куб.
год	квартал	У, млн. руб.						год	квартал	У, млн. руб.
		126,1								156,1
		121,3								121,3
		118,3								118,3
		121,5								121,5
		138,5								168,5
		134,2								134,2
		127,4								127,4
		132,5								132,5
		149,5								159,5
		148,1								148,1
		132,1								132,1
		145,8								145,8
		156,4								186,4
		150,3								150,3
		138,2								138,2
		151,3								151,3
		169,3								189,3
		160,8								160,8
		155,1								155,1
		169,7								169,7
		185,4								195,4
		175,1								175,1
		162,3								162,3
		157,3								157,3
Вариант 7								Вариант 8
Данные о заготовках леса, тыс. м куб.					Данные о заготовках леса, тыс. м куб.
год	квартал	У, тыс. м куб.						год	квартал	У, тыс. м куб.
		148,5								188,5
		134,2								164,2
		127,4								127,4
		132,5								132,5
		147,5								177,5
		148,1								158,1		&n