Временные ряды в эконометрических исследованиях

Большинство эконометрических моделей строится как динамические эконометрические модели. Это означает, что моделирование причинно-следственных связей между пе­ременными осуществляется во времени, а исходные данные представлены в форме временных рядов.

Временной ряд 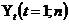- ряд значений какого-либо показателя за несколько последовательных промежутков времени.

Каждый временной ряд 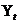складывается из следую­щих основных компонентов:

1) Тенденции, характеризующей общее направление динамики изучаемого явления. Аналитически тенденция выражается некоторой функцией времени, называемой трендом .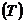

2) Циклической или периодической компоненты, ха­рактеризующей циклические или периодические колебания изучаемого явления. Например: значения макроэкономиче­ских показателей зависят от того, в какой фазе бизнес-цикла находится экономика. Объем продаж некоторых товаров подвержен сезонным колебаниям .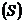

3) Случайной компоненты, которая является результа­том воздействия множества случайных факторов .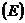

Тогда уровень ряда можно представить как функцию от этих компонент: .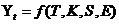

В зависимости от взаимосвязи между этими компо­нентами может быть построена либо аддитивная модель: 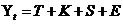, либо мультипликативная модель: 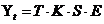ряда динамики.

Пусть нам даны поквартальные данные об объеме вы­пуска некоторого товара некоторой фирмой - Y (усл.ед.) за 3 года:

Таблица 4 – Исходные данные об объеме вы­пуска товара фирмой

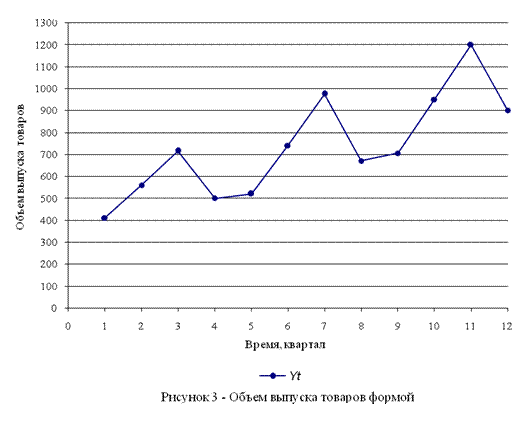
График данного временного ряда (рисунок 3) свидетельствует о наличии сезонных колебаний (период колебаний равен 4) и общей возрастающей тенденции уровней ряда. Объем выпускаемой продукции в весенне-летний период выше, чем в осенне-зимний период. Поскольку амплитуда сезонных колебаний примерно постоянна, можно предположить существование аддитивной модели.

Автокорреляция - корреляционная связь между после­довательными уровнями одного и того же ряда динамики (сдвинутыми на определенный промежуток времени L - лаг).

Лаг (сдвиг во времени) определяет порядок коэффициента автокорреляции. Если 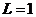, то имеем коэффициент ав­токорреляции 1-ого порядка 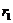, если 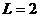, то коэффициент автокорреляции 2-ого порядка 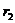и т.д. Следует учитывать, что с увеличением лага на единицу, число пар значе­ний, по которым рассчитывается коэффициент автокорреляции, уменьшается на единицу. Поэтому обычно рекомендуют максимальный порядок коэффициента автокорреляции рав­ный n/4.

Рассчитав несколько коэффициентов автокорреляции, можно определить лаг 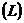, при котором автокорреляция наиболее высокая, выявив тем самым структуру временного ряда. Если наиболее высоким оказывается значение 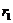, то исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался 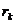, то ряд содержит (помимо тенденции) колебания периодом k. Если ни один из коэффициентов автокорреляции k не является значимым, можно сделать одно из двух предположений:

- либо ряд не содержит тенденции и циклических ко­лебаний, а его уровень определяется только случайной компонентой;

- либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.

Последовательность коэффициентов автокорреляции 1, 2 и т.д. порядков называют автокорреляционной функци­ей временного ряда. График зависимости значений коэффи­циентов автокорреляции от величины лага (порядка коэф­фициента автокорреляции) называют коррелограммой.

Для выявления закономерных колебаний внутри года при выполнении контрольной работы рекомендуется рассчитывать не меньше 4-х уровней коэффициентов автокор­реляции.

Определим коэффициент автокорреляции 1-го порядка, используя формулу линейного коэффициента корреляции.

,

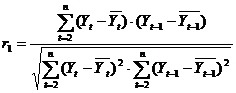где

; ,

,

,

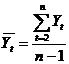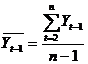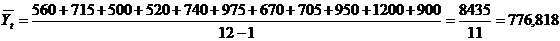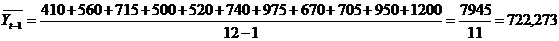Промежуточные расчеты по определению коэффициента автокорреляции первого порядка приведены в таблице 5.

Таблица 5- Вспомогательные расчеты по определению коэффициента автокорреляции первого порядка.

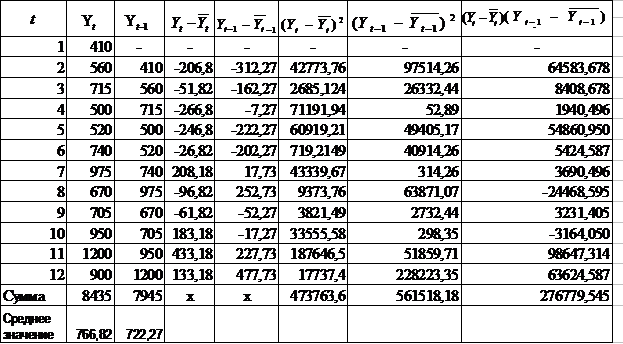
Таким образом, ,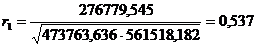

Далее определим коэффициент автокорреляции второго порядка по формуле:

,

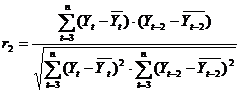где

; ,

,

,

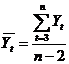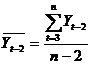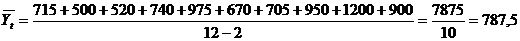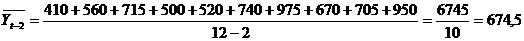Промежуточные расчеты по определению коэффициента автокорреляции второго порядка приведены в таблице 6.

Таблица 6 - Вспомогательные расчеты по определению коэффициента автокорреляции второго порядка.

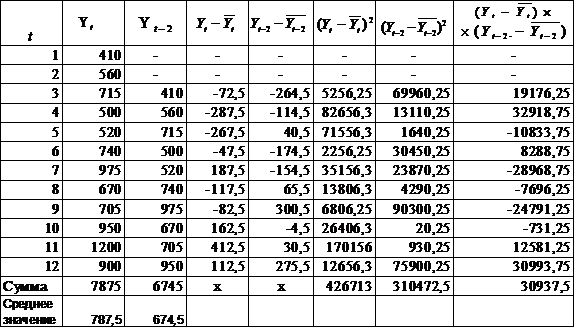
Таким образом, .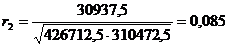

Аналогично вычисляются коэффициенты автокорреляции третьего, четвертого и т.д. порядка. Результаты расчетов и коррелограмма представлены в таблице 7.

Таблица 7 – Автокорреляционная функция и коррелограмма временного ряда объема вы­пуска товара фирмой

Вывод: в данном ряду динамики имеется тенденция и периодические колебания с периодом (L) равным 4, т.е. имеют место сезонные колебания.

Построение аддитивной модели временного ряда с сезонными колебаниями.

Обратимся к данным об объеме выпуска товара некоторой фирмой за последние три года, представленным в таблице 4.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

а) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (графа 3 таблицы 8);

б) разделив полученные суммы на 4, найдем скользящие средние (графа 4 таблицы 8). Отметим, что полученные таким образом выровненные значения уже не содержат сезонной компоненты;

в) приведем эти значения в соответствие с фактическими момен­тами времени, для чего найдем средние значения из двух последовательных скользящих средних - центрированные скользящие средние (графа 5 таблицы 8).

Таблица 8 - Расчет оценок сезонной компоненты в аддитивной модели.

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (графа 6 таблицы 8). Используем эти оценки для расчета значений сезонной компоненты S (таблица 9). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.

Таблица 9 - Расчет значений сезонной компоненты в аддитивной модели.

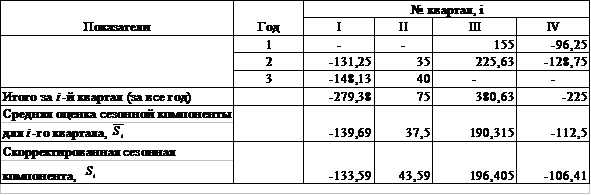
Для данной модели имеем:

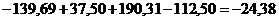
Определим корректирующий коэффициент: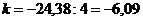

Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:

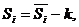где ,

Проверим условие равенства нулю суммы значений сезонной компоненты:

.

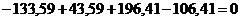Таким образом, получены следующие значения сезонной компоненты:

I квартал: ;

II квартал: ;

III квартал: ;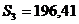

IV квартал: .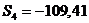

Занесем полученные значения в таблицу 10 для соответствующих кварталов каждого года (графа 3).

Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины 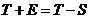(графа 4 таблицы 10). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

Таблица 10 - Расчет выровненных значений T и ошибок E в аддитивной модели.

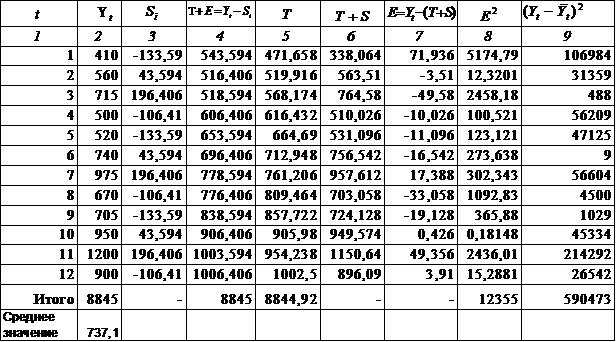
Шаг 4. Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда 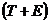с помощью линейного тренда (расчеты выполнены с помощью Ms Excel). Результаты аналитического выравнивания следующие:

,

.

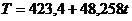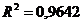Подставляя в это уравнение значения t = 1, ..., 16, найдем уровни Τ для каждого момента времени (графа 5 таблицы 10). График уравнения тренда приведен на рисунке 4.

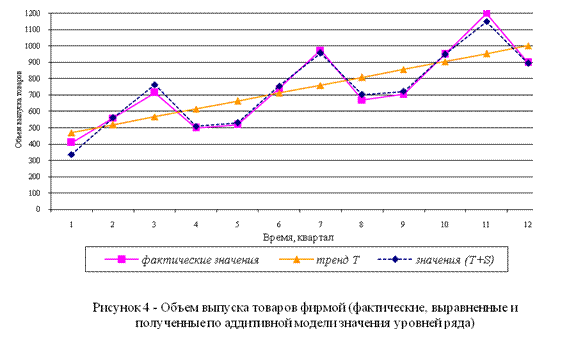
Рисунок 4 - Объем выпуска товаров фирмой (фактические, выровненные и полученные по аддитивной модели значения уровней ряда)

Шаг 5. Найдем значения уровней ряда, полученные по адди­тивной модели. Для этого прибавим к уровням T значения сезон­ной компоненты для соответствующих кварталов. Графически значения 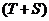представлены на рисунке 4.

Шаг 6.В соответствии с методикой построения аддитивной модели расчет ошибки производится по формуле:

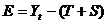
Это абсолютная ошибка. Численные значения абсолютных ошибок приведены в графе 7 таблицы 10.

Для оценки качества построенной модели или для выбора наилучшей модели используется ошибка ε.

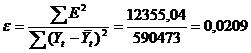
Следовательно, можно сказать, что аддитивная модель объясняет 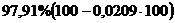общей вариации временного ряда.