Марковские случайные процессы

При исследовании различных операций с точки зрения выбора оптимального решения часто возникают ситуации, когда обстановка приведения операции характеризуется случайными неконтролируемыми факторами.
В этом случае операция развивается по схеме случайного процесса, протекание которого зависит от сопровождающих операцию случайных факторов.

Количественно случайный процесс описывается случайной функцией времени t, которая может принимать различные значения с заданным распределением вероятностей. Т.о. для любого t=ti значение
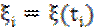является случайной величиной.

Случайный процесс определяется совокупностью функций времени и законами, характеризующими свойства этой совокупности. Каждая из функций этой совокупности называется реализацией случайного процесса. Реализация обозначается

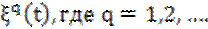
В зависимости от того, принадлежат ли возможные значения времени t и реализации
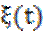дискретному множеству чисел или интервалу действительных чисел, различают четыре типа случайных процессов:

1. Случайный процесс общего типа:
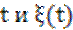   могут принимать любые значения.
2. Дискретный случайный процесс:
   t-непрерывно, а значения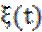 дискретны.
3. Случайная последовательность общего типа:
   t-дискретно, а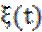 принимает любые значения.
4. Дискретная случайная последовательность:
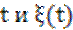   дискретны.

Для описания случайного процесса используют функции распределения:

одномерная интегральная функция распределения вероятностей случайного процесса 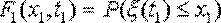и плотность вероятности .
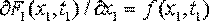Функции F1(x1,t1) и f(x1,t1) являются простейшими характеристиками, т.к. описывают случайный процесс в фиксированные моменты времени. Для более полной характеристики случайного процесса необходимо знать связь между вероятными значениями случайной функции в произвольные моменты времени t1, t2, : tn.

Определим n-мерную функцию распределения вероятностей случайного процесса 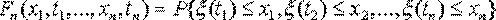Если Fn() имеет частные производные 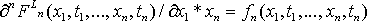то эта производная называется n-мерной плотности вероятности случайного процесса. Имеет место очевидное равенство

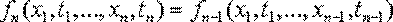
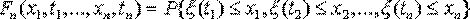-условие плотности вероятности, которое зависит от значений случайного процесса в предшествующие моменты времени начиная с начального момента времени t1 и кончая моментом tn-1.
Случайный процесс будет марковским, если выполняется условие 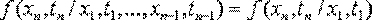В этом случае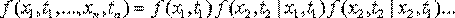
Условная плотность вероятности 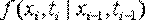называется плотностью вероятности перехода.Если плотность вероятности перехода зависит от разности 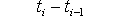и не зависит от конкретных значений ti, ti-1 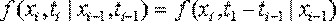то такой процесс называется однородным. В исследовании операций большое значение имеют так называемые марковские случайные процессы с дискретными состояниями и непрерывным временем. В этом случае все его возможные состояния Q1,Q2,... можно перенумеровать.
Переход из состояния в состояние происходит мгновенно, а моменты времени переходов являются случайными.