Исследование характеристик трубопроводов при
Различных режимах течения
Цель работы: экспериментальное определение потерь напора по длине простого трубопровода, построение его напорной характеристики, получение экспериментального значения коэффициентов гидравлического сопротивления и трения, сравнение полученных значений с расчетными при ламинарном и турбулентном режимах течения.
Теоретическое введение
Различают два режима движения жидкости: ламинарный и турбулентный. При ламинарном (от лат. laminare – слоистый) режиме жидкость движется отдельными параллельными струями, не перемешиваясь между собой. При турбулентном (от лат. turbulentus – бурный, беспорядочный) режиме, струи жидкости перемешиваются между собой.
В 1883 году английский физик О. Рейнольдс теоретически обосновал закономерности ламинарного и турбулентного режимов движения жидкости. Существование ламинарного и турбулентного режимов движения жидкости определяется безразмерным параметром:
,
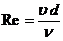где υ – скорость движения жидкости; d – диаметр трубопровода; ν – кинематическая вязкость жидкости.
Впоследствии данный безразмерный параметр получил название число Рейнольдса.
По данным О. Рейнольдса имеется некоторое критическое число Рейнольдса Reкр, при котором режим ламинарный переходит в турбулентный и наоборот. Для труб круглого сечения Reкр = 2320.
Ламинарный режим характеризуется условием Reкр ≤ 2320. Турбулентный – Reкр > 2320.
Знание режимов движения жидкости является важным, так как при различных режимах движения наблюдаются свои закономерности потерь напора и давления:
– при ламинарном режиме потери пропорциональны скорости Δh = А υ;
– при турбулентном режиме Δh = В υn
где A, B – коэффициенты пропорциональности; n – показатель, зависящий от степени турбулизации потока.
Потери напора на трение представляют собой необратимое убывание энергии потока жидкости или газа, связанное с преодолением сил вязкости. В любом потоке жидкости, ограниченном твердыми стенками, скорости в поперечном сечении распределены неравномерно. По оси канала или трубы скорость максимальна, а на стенках она равна нулю. Поэтому смежные частицы жидкости движутся с различными скоростями и под действием сил вязкости возникают касательные напряжения трения, на преодоление которых затрачивается часть энергии (напора) потока жидкости.
Потери напора на трение вычисляют по формуле Дарси–Вейсбаха
,
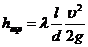где l – коэффициент сопротивления трения; l, d – длина и диаметр трубопровода, м; υ – средняя скорость течения, м/с; g = 9,81 м/с2 – ускорение свободного падения.
Потери напора на трение прямо пропорциональны длине трубопровода, поэтому их иногда называют линейными. Коэффициент сопротивления трения зависит от вязкости и режима течения жидкости, формы и размеров сечения, а также от величины шероховатости стенок трубы.
Коэффициент сопротивления трения или коэффициент Дарси, в случае ламинарного режима течения жидкости зависит только от числа Рейнольдса и для любых ньютоновских жидкостей вычисляется по формуле Пуазейля
.
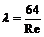При турбулентном режиме течения коэффициент Дарси имеет более сложную зависимость и определяется по эмпирическим формулам.
Потери напора на трение, помимо всего прочего, зависят ещё и от величины шероховатости стенок труб, поэтому все типы труб условно подразделяют на гладкие и шероховатые. К первым относят стеклянные, пластмассовые, латунные, медные и прочие виды труб, у которых величина средней шероховатости не более 0,1 мм. Остальные виды труб относятся к шероховатым трубам.
Гладкие трубы
Поскольку величина шероховатости у этих труб невелика и намного меньше толщины вязкого ламинарного подслоя, то основной турбулентный поток не касается стенок трубы и шероховатость на величину потерь напора влияния не оказывает. В этом случае коэффициент сопротивления трения зависит только от величины числа Рейнольдса и может быть вычислен по одной из нижеприведенных формул.
Если число Рейнольдса находится в пределах 2320 – 105, то можно воспользоваться формулой Блазиуса
.
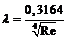Если число Рейнольдса находится в пределах 2320 – 106, тогда можно воспользоваться формулой П.К. Конакова
.
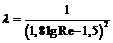Трубы шероховатые
Коэффициент сопротивления трения при течении жидкости в этих трубах в основном зависит от величины числа Рейнольдса и относительной шероховатости, которая представляет собой отношение
,
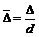где D – средняя шероховатость стенок трубы, мм; d – диаметр трубы, мм.
В зависимости от влияния числа Рейнольдса и относительной шероховатости на величину коэффициента сопротивления трения различают три зоны сопротивления трения.
Зона гидравлически гладких труб
Эта зона сопротивления имеет место при небольших числах Re, когда оно находится в пределах
.
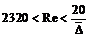В этом случае степень турбулизации потока невелика и вязкий подслой имеет толщину, превышающую величину шероховатости стенок трубы. Поэтому шероховатость не оказывает никакого влияния на турбулентное ядро потока, а потери напора на трение в этой зоне зависят только от числа Рейнольдса. Иными словами, шероховатые трубы в этой зоне сопротивления трения "работают" так же, как гладкие трубы. Коэффициент сопротивления трения в этой зоне можно вычислять по формуле Блазиуса или П.К. Конакова.
Зона переходного сопротивления
Эта зона сопротивления имеет место, когда число Рейнольдса находится в пределах
.
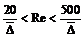В этой зоне сопротивления вследствие значительной турбулентности поток жидкости частично разрушает вязкий подслой, толщина его становится меньше величины шероховатости, поэтому выступающие за пределы вязкого подслоя "пики" шероховатости оказывают дополнительное сопротивление потоку жидкости. Коэффициент сопротивления трения в этом случае зависит и от числа Рейнольдса, и от величины относительной шероховатости стенок трубы и вычисляется по формуле А.Д. Альтшуля
.
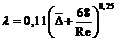Зона квадратичного сопротивления
Эта зона сопротивления имеет место при больших числах Рейнольдса, когда оно превышает значение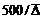 
. В этом случае вследствие значительной турбулентности потока толщина вязкого подслоя становится намного меньше величины шероховатости стенок трубы, поэтому её влияние на потери напора становится преобладающим. Возрастание числа Рейнольдса не приводит к увеличению потерь напора, так как степень турбулентности потока жидкости в этой зоне имеет предельное значение, т.е. наступает автомодельный режим сопротивления. Коэффициент сопротивления трения для этой зоны вычисляют по эмпирической формуле Б.Л. Шифринсона
.
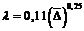Порядок выполнения работы
Для данной работы используется стенд № 1 ЭМЖ-09-14ЛР-01 «Основы гидравлики», устройство и работа которого представлены в лабораторной работе № 1 лабораторного практикума «Металлургическая теплотехника» часть 1.
Выполняется для трубопровода Т1 с внутренним диаметром dвн = 15 мм и Т2 (внутренний диаметр dвн = 11 мм).
1. Полностью закрыть задвижки 31, 32, 33, 34, 35, 36, 37, 38 и краны КР4, КР5, КР8, КР12. Краны КР6, КР7, КР10, КР11, КР14 полностью открыть.
2. Повернуть переключатель насоса НЗ в крайнее правое положение и включить питание переключением соответствующего тумблера на блоке управления.
3. Дождаться наполнения напорной секции накопительного бака, вплоть до возникновения перелива.
4. Откручивая рукоятку задвижки З1 установить уровень жидкости в пьезометре №1 (Нп1) в соответствие с таблицей 3.
5. Записать в таблицу 3 показания пьезометра №2 для трубопровода Т1 ОВД.
6. Закрыть кран КР10. Измерить время ∆t заполнения объема V жидкости, поступающей в мерную емкость ЕМ1. Записать значения в таблицу 3. Открыть кран КР10.
7. Повторяя работы по п. 4, 5 и 6 выполнить замеры для всего интервала Нп1 из таблицы 4.
8. Закрыть задвижку 31.
9. Откручивая рукоятку задвижки З2 установить уровень жидкости в пьезометре №2 (НП2) в соответствие с таблицей 4.
10. Записать в таблицу 4 показания пьезометра №4 для трубопровода Т2 (Нп4).
11. Закрыть кран КР9. Измерить время ∆t заполнения объема V жидкости, поступающей в мерную емкость ЕМ2. Записать значения в таблицу 4. Открыть кран КР9.
12. Отворачивая рукоятку задвижки З2 установить следующую величину пьезометрического напора в сечении 3 (см. таблицу 4).
13. Повторяя работы по п.9, 10, 11, 12 выполнить замеры для всего интервала Нп3.
14. Закрыть З2.
15. Выключить питание насоса НЗ.